在控制理论中,为了描述线性定常系统的输入-输出关系,最常用的函数是所谓的传递函数。传递函数的概念只适用于线性定常系统,在某些特定条件下也可以扩充到一定的非线性系统中去。 线性定常系统的传递函数,定义初始条件为零时,输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。设有一线性定常系统,它的微分方程是  | (2-1) |
式中y是系统的输出量,x是系统的输入量。初始条件为零时,对方程(2-1)两端进行拉普拉斯变换,就可以得到该系统的传递函数为: 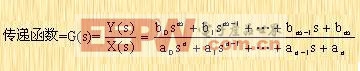 | (2-2) |
传递函数是一种以系统参数表示的线性定常系统的输入量与输出量之间的关系式,它表达了系统本身的特性,而与输入量无关。传递函数包含着联系输入量与输出量所必需的单位,但它不能表明系统的物理结构(许多物理性质不同的系统,可以有相同的传递函数)。 传递函数分母中s的最高阶数,就是输出量最高阶导数的阶数。如果s的最高阶数等于n,这种系统就叫n阶系统。 例2-1 图2-1所示为一弹簧阻尼系统,阻尼器是一种产生粘性磨擦或阻尼的装置。它由活塞和充满油液的缸体组成。活塞和缸体之间的任何相对运动,都将受到油液的阻滞,因为这时油液必须从活塞的一端,经过活塞周围的间隙(或通过活塞上的专用小孔),而流到活塞的另一端。阻尼器主要用来吸收系统的能量。被阻尼器吸收的能量转变为热量而散失掉,而阻尼器本身不贮藏任何动能或位能。
下面来推导这一系统的传递函数。设系统的输入量为外力x(t),输出量为质量的位移y(t),按下列步骤进行推导: 1. 写出系统的微分方程。
2. 假设全部初始条件等于零,取微分方程的拉普拉斯变换。
3. 求输出Y(s)与输入量X(s)之比。这一比值就是传递函数。 为了推导线性常系数微分方程,假设阻尼器的磨擦力与 成正比,并设弹簧为线性弹簧,即弹簧力与y成正比。在这个系统中,m表示质量,f表示粘性磨擦系数,而k表示弹簧刚度。
解 牛顿定律是机械系统中的基本定律。在平移系统中,牛顿定律可表示如下:
ma=ΣF=x-Fs-Ff
其中Fs=ky,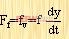
a表示加速度,f表示力。
把牛顿定律应用到这一系统可得 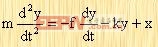
或 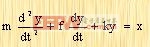 | (2-3) |
对方程(2-3)中每一项取拉普拉斯变换,得出
如果设初始条件等于零,即y(0)=0, (0)=0,即可得出方程(2-3)的拉普拉斯变换:
取Y(s)与X(s)之比,即可得到系统的传递函数: 例2-2 机械转动系统 设有一系统,如图2-2所示。它由惯性负载和粘性磨擦阻尼器组成。J为转动惯量,f为粘性磨擦系数,ω为角速度,T为作用到系统上的转矩。 解 对于机械转动系统,其运动方程可写成: 其微分方程为: 初始条件为零时,取方程(2-4)的拉普拉斯变换: 取θ(s) 与T(s)之比,即可得到系统的传递函数:
例2-3
图2-3所示为一由电感L、电阻R和电容C组成。 解: 在理想条件下,可得到此电路的电压平衡方程式: 由于 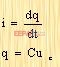 式中,q为电荷量,C为电容。式(2-5)可改写为 式中,q为电荷量,C为电容。式(2-5)可改写为 初始条件为零时,取方程(2-5)的拉普拉斯变换: 取U(s)与Uc(s) 之比,即可得到系统的传递函数: |