控制系统的数学模型

在方块图中，通过函数方块，可以将所有的系统变量联系起来。"函数方块"或简称为"方块"，是对加到方块上的输入信号的一种运算符号，运算结果以输出量表示。元件的传递函数，通常写进相应的方块中，并以标明信号流向的箭头，将这些方块连接起来。应当指出，信号只能沿箭头方向通过。这样，控制系统的方块图就清楚地表示了它的单向特性。

T为惯性环节的时间常数，K为比例系数。
当输入信号为单位阶跃函数时，其环节的输出为

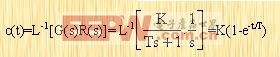图2-4表示了一个方块图单元。指向方块的箭头表示输入，而从方块出来的箭头则表示输出。在这些箭头上标明了相应的信号。

应当指出，方块输出信号等于输入信号与方块中传递函数的乘积。

用方块图表示系统的优点是：只要依据信号的流向，将各元件的方块连结起来，就能够容易地组成整个系统的方块图，通过方块图，还可以评价每一个元件对系统性能的影响。

总之，方块图比物理系统本身更容易体现系统的函数功能。方块图包含了与系统动态特性有关的信息，但它不包括与系统物理结构有关的信息。因此，许多完全不同和根本无关的系统，可以用同一个方块图来表示。

应当指出，在方块图中没有明显表示出系统的主能源，而且对于一定的系统来说，方块图也不是唯一的。由于分析角度的不同，对于同一个系统，可以画出许多不同的方块图。

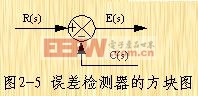
误差检测器 误差检测器产生的输出信号，等于控制系统的参考输入信号与反馈信号之差。在设计中，选择误差检测器是一件很重要的工作，需要仔细确定。因为误差检测器中的任何缺陷，都必然会降低整个系统的性能。图2-5表示了误差检测器的方块图。

需要注意的是，图中进行相加或相减的一些量，应具有相同的量纲和单位。

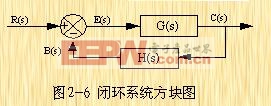
闭环系统方块图 在图2-6上，表示了一个闭环系统的方块图。输出量C(s)反馈到相加点，并且在相加点与参考输入量R(s)进行比较。系统的闭环性质，在图上清楚地表示了出来。在这种情况下，方块的输出量C(s)，等于方块的输入量E(s)乘以传递函数G(s)。

任何线性控制系统，都可以用由方块、相加点和分支点组成的方块图来表示。所谓分支点，就是由方块出来的输出信号，从这一点起同时进入另一个方块或相加点。

当输出量反馈到相加点与输入量进行比较时，必须将输出信号转变为与输入信号相同的形式。例如，在温度控制系统中，输出信号通常为被控温度。具有温度量纲的输出信号，在与输入信号进行比较之前，必须转变为力或位置。这种转换由反馈元件来完成，反馈元件的另一个重要作用，是在输出量与输入量进行比较之前，改变输出量。对于正在讨论的例子，反馈到相加点与输入量进行比较的反馈信号为B(s)=H(s)C(s)。

反馈信号B(s)与作用误差信号E(s)之比，叫做开环传递函数。即

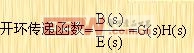输出量C(s)与作用误差信号E(s)之比，叫做前向传递函数，因而

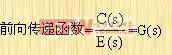如果反馈传递函数等于1，那么开环传递函数与前向传递函数相同。在图2-6所示系统中，输出量C(s)与输入量R(s)的关系，可推导如下：

C(s)=G(s)E(s)
E(s)=R(s)-B(s)=R(s)-H(s)C(s)

从上述方程中消去E(s)，得

C(s)=G(s)[R(s)-H(s)C(s)]

于是可得

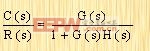(2-17)

C(s)与R(s)之间的传递函数，叫做闭环传递函数。这一传递函数，将闭环系统的动特性，与前向通道元件和反馈通道元件的动态特性联系在一起了。

由方程（2-17），可求得C(s)为

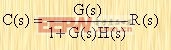因此，闭环系统的输出量，显然取决于闭环传递函数和输入量的性质。

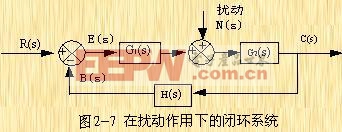
扰动作用下的闭环系统 图2-7为一个在扰动作用下的闭环系统。当两个输入量（参考输入量和扰动量）同时作用于线性系统时，可以对每一个输入量单独地进行处理，将与每一个输入量单独作用时相应的输出量叠加，即可得到系统的总输出量。每个输入量加进系统的形式，用相加点上的加号或减号来表示。

现在来讨论图2-7上表示的系统。在研究扰动量N(s)对系统的影响时，可以假设系统在开始时是静止的，并且假设无误差信号，这样就可以单独计算系统对扰动的响应CN(s)。这一响应可由下式求得：

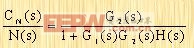另一方面，在研究系统对参考输入量的响应时，可以假设扰动量等于零。这时系统对参考输入量R(s)的响应CR(s)可由下式求得：

将上述两个单独的响应相加，就可以得到参考输入量和扰动量同时作用时的响应。换句话说，参考输入量R(s)和扰动量N(s)同时作用于系统时，系统的响应C(s)为

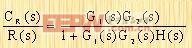另一方面，当G1(s)G2(s)H(s)的增益增大时，闭环传递函数CR(s)/R(s)趋近于1/H(s)。这表明，当 >>1时，闭环传递函数CR(s)/R(s)将变成与G1(s)和G2(s)无关，而只与H(s)成反比关系，因此G1(s)和G2(s)的变化，不影响闭环传递函数CR(s)/R(s)。这是闭环系统的另一个优点。可