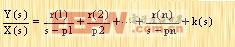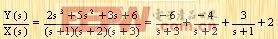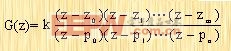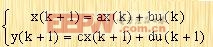控制系统的数学模型
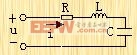 |
其状态方程可以用下列方程描述:
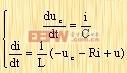 |
|
由上式可知,如果已知uc(t)和i(t)的初始值,以及在t3t0时的外加输入信号,就能够完全唯一地确定在t3t0时的任何时间的系统状态。状态方程也可以写成矩阵方程的形式。例如:
 |
|
通常,用x表示状态矢量,用x1,x2,... 表示其分量。对于上式,如令
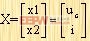 |
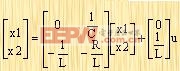
式(2-26)又可写为
 |
|
此处其输出方程为
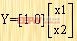 |
|
此处 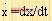
需要指出的是,从理论上讲,描述系统状态的状态变量的选择不是唯一的,可以有无穷多个解。
2.7.2 线性定常控制系统的状态方程描述
本教材研究对象主要为线性定常系统,这里简单介绍一下线性定常系统的状态方程:
1. 单输入单输出线性定常系统状态方程
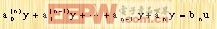 | (2-29) |
式中y为输出量,x为输入量,a1、a2、...、an和bn为常系数。
当令
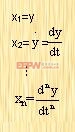 |
此时,可将式(2-29)改写为n个一阶微分方程,即
 |
或用矩阵方程表示:
 |
上式可简写为
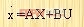 |
式中
 |
系统的输出方程为
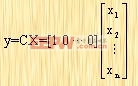 |
2. 多变量线性定常系统状态方程
推广到多变量线性定常系统的一般情况,此时的系统传递函数可表示为:
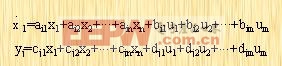 |
式中 i=1,2,...,n;j=1,2,...,m。可用矩阵方程表示为:
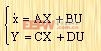 |
此处
 |
2.7.3线性定常系统状态空间表达式的结构图和信号流图
系统的状态方程和输出方程也可以用结构图的方式表达出来,它形象地说明了系统输入、输出和系统状态之间的信息传递关系。在采用模拟计算机对系统仿真时,它更是一个得力的工具。图2- 16所示为n维线性定常系统的结构图。
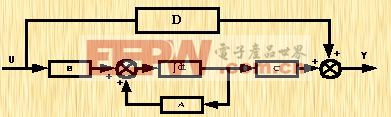 |
图2-16 n维线性定常系统的结构图 |
同样,也可以画出n维线性定常系统的信号流图(见图2-17所示)。
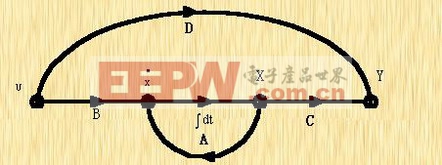 |
图2-17 n维线性系统的信号流图 |
2.7.3线性定常系统状态空间表达式的结构图和信号流图
下面仔细分析一下单输入单输出系统的传递函数与状态空间之间的关系:
设所要研究系统的传递函数为:
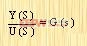 |
该系统在状态空间中可以用下列方程表示:
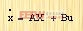 | (2-30) |
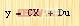 | (2-31) |
式中X为状态向量,u为输入量,y为输出量。则当满足零初始条件时,式(2-30)及(2-31)的拉普拉斯变换为:
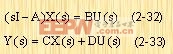 |
用(sI-A)-1左乘式(2-32)等号两边,得到:
X(s)=(sI-A)-1BU(s) (2-34)
把方程(2-34)代入(2-33),得到
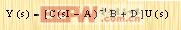 | (2-35) |
由方程(3-35)可以看出
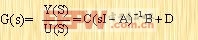 |
这就是以A、B、C和D的形式表示的传递函数。应该指出,传递函数矩阵具有不变性,亦即,对状态方程进行线性变换后,其对应的传递函数矩阵应该不变,从而保证了所描述系统的输入-输出特性不变。
数学模型的MATLAB描述
|
- 基于单片机实现摄像机运动控制系统的设计(05-30)
- 一种智能型全自动快速充电机的设计(07-20)
- 基于USB接口的数据采集与控制系统设计(09-21)
- 单级倒立摆控制系统的稳定性算法设计(03-02)
- 利用GaAs PHEMT设计MMIC LNA(11-15)
- 力控组态软件在光伏发电系统中的应用(02-24)

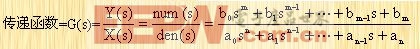
 的系统。
的系统。
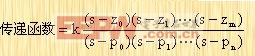 时
时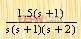 的系统。
的系统。
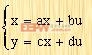 时
时