控制系统的数学模型

y=f(x) （2-6）

如果系统的额定工作状态相应于 ，，那么方程（2-6）可以在该点附近展开成泰勒级数：

式中都在x=df/dx,d²f/dx²,… 点进行计算。如果x- 很小，可以忽略x- 的高阶项。因此方程可以写成

方程（2-8）可以改写成

上式说明y- 与x- 成正比。方程（2-9）就是由方程（2-6）定义的非线性系统的线性数学模型。下面来研究另一种非线性系统，它的输出量y是两个输入量x1和x2的函数，因而

为了得到这一非线性系统的线性近似关系，将方程（2-10）在额定工作点, 附近展开成泰勒级数。这时方程（2-10）可写成

式中偏导数都在x₁=,x₂=上进行计算。在额定工作点附近，近似将高阶项忽略。于是在额定工作状态附近，这一非线性系统的线性数学模型可以写成

这里介绍的线性化方法只有在工作状态附近才是正确的。当工作状态的变化范围很大时，线性化方程就不合适了，这时必须使用非线性方程。应当特别注意，在分析和设计中采用的具体数学模型，只有在一定的工作条件下才能精确表示实际系统的动态特性，在其他工作条件下它可能是不精确的。

比例环节又称放大环节，其传递函数为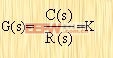

(2-11)

这表明，输出量与输入量成正比，动态关系与静态关系都一样，不失真也不迟延，所以又称为"无惯性环节"或"放大环节"。比例环节的特征参数只有一个，即放大系数K。工程上如无弹性变形的杠杆传动、电子放大器检测仪表、比例式执行机构等都是比例环节的一些实际例子。

2.4.2惯性环节

惯性环节又称非周期环节，其传递函数为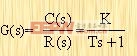

(2-12)

T为惯性环节的时间常数，K为比例系数。
当输入信号为单位阶跃函数时，其环节的输出为

它是一条指数曲线，当时间t=3T~4T时，输出量才接近其稳态值。实际系统中，惯性环节是比较常见的，例如直流电机的励磁回路等。

2.4.3积分环节

积分环节的传递函数为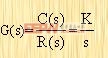

(2-13)

在单位阶跃输入的作用下，积分环节的输出c(t)为

这表明，只要有一个恒定的输入量作用于积分环节，其输出量就与时间成正比地无限增加。积分环节具有记忆功能，当输入信号突然除去时，输出总要变化下去。在控制系统设计中，常用积分环节来改善系统的稳态性能。

2.4.4微分环节

微分环节的传递函数为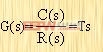

(2-14)

理想微分环节的输出与输入量的变化速度成正比。在阶跃输入作用下的输出响应为一理想脉冲（实际上无法实现），由于微分环节能预示输出信号的变化趋势，所以常用来改善系统的动态特性。

实际上可实现的微分环节都具有一定的惯性，其传递函数如下：

它有一个负极点和一个位于S平面原点的零点。实际微分环节在单位阶跃输入作用下的输出响应为

2.4.5振荡环节

振荡环节的传递函数为

(2-15)

或

式中，T为振荡环节的时间常数；K为放大系数；ζ为振荡环节的阻尼比； 称为无阻尼自然振荡频率。

2.4.6延迟环节

延迟环节的传递函数为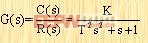

(2-16)

延迟环节在单位阶跃输入作用下的输出响应为c(t)=1(t-T)

即输出完全复现输入，只是延迟了T时间。T为延迟环节的特征参数，称为"延迟时间"或"滞后时间"。

以上介绍了六种典型环节，这是控制系统中最见的基本环节

方块图 :
系统方块图，是系统中每个元件的功能和信号流号的图解表示。方块图表明了系统中各种元件间的相互关系。方块图优于纯抽象的数学表达式，因为它能够清楚地表明实际系统中的信号流动情况。

在方块图中，通过函数方块，可以将所有的系统变量联系起来。"函数方