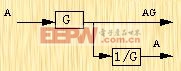
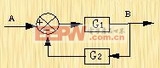
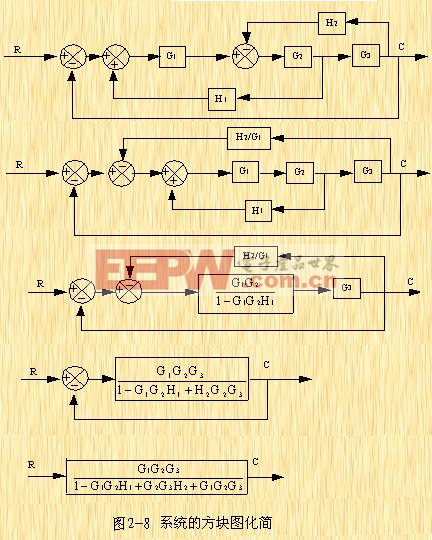
方块图对于图解表示控制系统,是很有用的。但是当系统很复杂时,方块图的简化过程是很繁杂的。信号流程图,是另一种表示复杂控制系统中系统变量之间关系的方法。这种方法是S.J.梅逊(Mason)首先提出的。
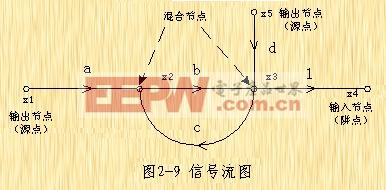
信号流图 信号流图,是一种表示一组联立线性代数方程的图。当将信号流图法应用于控制系统时,首先必须将线性微分方程变换为以s为变量的代数方程。 信号流图是由网络组成的,网络中各节点用定向支线段连接。每一个节点表示一个系统变量,而每两节点之间的联结支路相当于信号乘法器。应当指出,信号只能单向流通。信号流的方向由支路上的箭头表示,而乘法因子则标在支路线上。信号流图描绘了信号从系统中的一点流向另一点的情况,并且表明了各信号之间的关系。 正如所料,信号流图基本上包含了方块图所包含的信息。用信号流图表示控制系统的优点,可以应用所谓梅逊增益公式。根据该公式,不必对信号流图进行简化,就可以得到系统中各变量之间的关系。 定义 在讨论信号流图之前,首先必须定义如下一些术语: 节点,节点用来表示变量或信号的点。
传输,两个节点之间的增益叫传输。
支路,支路是连接两个节点的定向线段。支路的增益为传输。
输出节点或源点,只有输出支路的节点,叫输出节点或源点。它对应于自变量。
输入节点或阱点,只有输入支路的节点,叫输入节点或阱点。它对应于因变量。
混合节点,既有输入支路,又有输出支路的节点,叫混合节点。
通道,沿支路箭头方向而穿过各相连支路的途径,叫通道。如果通道与任一节点相交不多于一次,就叫做开通道。如果通道的终点就是通道的起点,并且与任何其它节点相交不多于一次,就叫做闭通道。如果通道通过某一节点多于一次,但是终点与起点在不同的节点上,那么这个通道既不是开通道,又不是闭通道。
回路,回路就是闭通道。
回路增益,回路中各支路传输的乘积,叫回路增益。
不接触回路,如果一些回路没有任何公共节点,就把它们叫做不接触回路。
前向通道,如果从输出节点(源点)到输入节点(阱点)的通道上,通过任何节点不多于一次,则该通道叫做前向通道。
前向通道增益,前向通道中,各支路传输的乘积,叫前向通道增益。 图2-9表示了节点、支路和支路传输。 信号流图的性质 下面介绍一些信号流图的重要性质。 1. 支路表示了一个信号对另一个信号的函数关系。信号只能沿着支路上的箭头方向通过。
2. 节点可以把所有输入支路的信号叠加,并把总和信号传送到所有支路。
3. 具有输入和输出支路的混合节点,通过增加一个具有单位传输的支路,可以把它变成输出节点来处理。(见图2-9,注意,具有单位传输的支路从x3指向另一个节点,后者也以x3表示。)当然,应当指出,用这种方法不能将混合节点改变为源点。
4. 对于给定的系统,信号流图不是唯一的。由于同一系统的方程可以写成不同的形式,所以对于给定的系统,可以画出许多种不同的信号流图。 信号流图代数 根据前面的定义,可以画出线性系统的信号流图。这样做时,通常将输出节点(源点)放在左面,而输入节点(阱点)放在右面。方程式的自变量和因变量,分别变为输出节点(源点)和输入节点(阱点)。支路的传输可由方程的系数得到。 |