关键区域分析与存储器冗余

要点

1.一个随机微粒缺陷的概率是布局特征间距的函数。因为存储器有相对致密的结构，它们天生就对随机缺陷更加敏感，于是就可能影响到器件的总良品率。

2.一款关键区域分析工具要能精确地分析出存储器冗余，就必须了解每个存储块中可用的修复资源，各个层与缺陷类型的故障模式的分解，以及这些模式与哪些修复资源相关联。

3.如果不使用冗余，就可能需要其它替代方法来提高良品率。这些方法包括让设计更小，或减少缺陷率。如果将冗余用于一个不会产生效益的设计中，那就是浪费片芯面积和测试时间，增加制造成本。

无论采用何种工艺的设计团队(无晶圆、轻晶圆或IDM(集成器件制造商))，都应解决降低设计对于制造问题敏感度的目标。一个设计向下游走得越远，就越不太可能解决某个制造问题，除非做昂贵的重新设计。在设计仍进行中就提示解决DFM(可制造性设计)问题，可以避免出现制造逐渐爬升的麻烦。

DFM的一个方面是确定某个物理设计(或布局)对于随机微粒缺陷的敏感程度。一个随机微粒缺陷的概率是布局特征间距的函数，因此，较紧密的间距会增加随机缺陷。由于存储器都有相对致密的结构，它们天生就对随机缺陷更为敏感，所以，SoC设计中的嵌入存储器可能影响到器件的总良品率。

了解如何在每个连续结点上采用关键区域分析正变得越来越重要。存储器正在越来越大，更小的尺寸会带来新的缺陷种类。某个折中可能在前代结点上工作良好，而在28nm结点时却得不到最佳结果。例如，虽然制造商都避免采用行冗余(rowredundancy)，因为他们认为这样会太费存取时间，但在28nm时，要获得可接受的良品率就必须采用这一技术。所有这些因素都使得作为设计工具的精细分析更有价值。

关键区域分析

关键区域是某种确定尺寸的微粒会造成某个功能故障的一个布局区，只取决于要仿真的布局以及微粒的尺寸范围。关键区域分析会根据布局特征的尺寸与间距、微粒尺寸以及晶圆厂测得的密度分布，计算出预期的平均故障数和良品率。除了传统的短路和开路计算以外，现在在关键区域分析上做的工作还包括过孔与接触故障。这些分析通常表明，过孔与接触故障是主要的故障机制。分析中也可以包括其它的故障机制，具体取决于晶圆厂提供的缺陷数据。

关键区域会随着缺陷或微粒的尺寸增长而增加。对于缺陷尺寸足够大的极限情况，整个芯片区都是关键区域。但实际上，大多数晶圆厂都会根据测试芯片或计量设备可以检测并测量的缺陷尺寸范围，限制可仿真的缺陷尺寸范围。

缺陷密度

半导体晶圆厂有多种方法来搜集缺陷密度数据。对于关键区域分析的使用，晶圆厂必须将缺陷密度数据转换为一种与分析工具兼容的格式。最常见的格式是下面的简单功率方程：D(X)=K/XQ，其中，K是从密度数据获得的一个常数，X是缺陷尺寸，而Q是下降幂。晶圆厂将每个层的开路与短路缺陷数据与这个支持关键区域分析的方程格式做曲线拟合。原则上，每个层都必须有一个缺陷密度和缺陷类型，它们将被用于关键区域分析。但实际上，对于采用相同的工艺步骤、层厚度，以及设计规则的各个层，通常会使用相同的缺陷密度值。

制造商也可能以表格形式提供缺陷密度数据，其中列出了每个缺陷的尺寸与密度值。一个简化的假设是，如缺陷尺寸超过了晶圆厂所拥有的数据范围，则缺陷密度为零。

计算ANF，良品率为了确定某个设计的平均故障数，制造商会使用一种支持关键区域分析的工具，如Mentor Graphics公司的Calibre，并在整个缺陷尺寸区间上针对各个层，用该工具提取出关键区。为此，制造商要测量布局，并确定某个给定尺寸微粒可能造成故障的所有区域。然后，工具要采用数学积分方法，用缺陷的尺寸与密度数据，计算出预期的故障平均数，公式为：

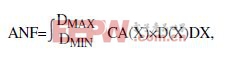
其中，ANF 是平均故障数；DMIN和DMAX分别是该层现有缺陷数据中的最小和最大缺陷尺寸； 而CA(X)和D(X)则分别是关键区域和缺陷密度数据。

一旦制造商计算出了平均故障数，通常会使用一个或多个良品率模型，对某个设计因缺陷受限的良品率做出一个预测。因缺陷受限的良品率不能考虑那些参数的良品问题，因此在尝试将此数值与实际片芯良品率做关联时，要特别小心。一种最简单而常用的良品率模型就是泊松(Poisson)模型：Y=E-ANF，其中，Y是良品率，E是一个常数，ANF是平均故障数。切割层(如触点和过孔)平均故障数与良品率的计算一般比其它层要简单。

大多数代工厂都会为设计中的所有单一过孔定义一个概率故障率，并假设过孔阵列不会失效。这种简化假设忽略了一个事实，即一个足够大的微粒可能造成多个故障， 不过，这样能大大简化对平