线性电路分析——网孔法详析

一． 定义
由人们主观设想的在网孔中流动的电流称为网孔电流，如图3-3-1中的iⅠ,iⅡ,iⅢ所示，它们的大小和参考方向均是任意设定的。以网孔电流为待求变量，根据KVL对各网孔列写出KVL约束方程而对电路进行分析的方法称为网孔电流法，简称网孔法。
二． 网孔电流变量的完备性与独立性
网孔电流变量的完备性是指电路中所有的支路电流都可由网孔电流求得。设各支路电流的大小和参考方向如图3-3-1中所示。若认为各网孔电流已被求出，则可得各支路电流为：

图3-3-1 网孔法可见网孔电流变量具有完备性。
网孔电流变量的独立性是指各网孔电流之间不受KCL约束，彼此独立，不能互求。例如对于节点a，我们可列出方程：
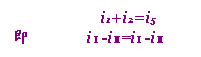
此式为一恒等式，即不管网孔电流iⅠ，iⅡ为何值都恒成立。对于其他节点也能得到类似结果，所以网孔电流变量具有独立性。
由于网孔电流变量具有完备性与独立性，所以可作为电路分析的变量。
三． 网孔KVL约束方程的列写与求解
在列写网孔的KVL约束方程时，应首先设定网孔电流的大小和参考方向。为了使所列方程有规律和容易写出，一般设定网孔电流的参考方向都是均为顺时针或均为逆时针，而且回路的循行方向就取为与网孔电流的参考方向一致。显然，网孔电流的个数以及所列KVL约束方程的个数，都一定是等于网孔数。例如对于图3-3-1所示电路可列出如下方程：

此方程称为网孔电压方程，简称网孔方程。解之即得各网孔电流iⅠ,iⅡ,iⅢ.
在上式中，令R11=R1+R4+R5，R22=R2+R5+R6，R33=R3+R4+R6，它们分别为网孔Ⅰ，网孔Ⅱ，网孔Ⅲ的自电阻，恒为正值；令R12=R21=-R5，R13=R31=-R4,R23=R32=-R6;R12,R21均称为网孔Ⅱ与网孔Ⅲ的互电阻。若设定网孔电流的参考方向均为同一方向（同为顺时针方向或同为逆时针方向），则互电阻均为负值，式（3-3-2）中即属此种情况；若设定网孔电流的参考方向不是均为同一方向（即有顺时针方向，有的为反时针方向），则互电阻中有的为正值，有的则为负值（若流过负电阻的相邻两个网孔电流的方向相同，则互电阻前取"+"号，否则取"-"号）。令us11= us1-us4，us22=-us2，us33= us3+us4，它们分别为网孔Ⅰ，网孔Ⅱ，网孔Ⅲ的所有电源电压升高的代数和。这样式（3-3-2）即可写为

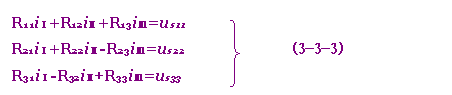
可见网孔方程的列写是很有规律的。将上式写成矩阵形式即为

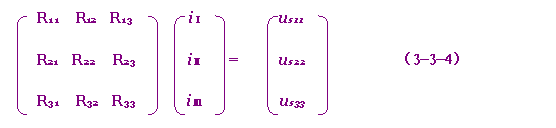
或 RiM=uM (3-3-5)

　

称为网孔电阻矩阵，为一对称阵：

称为网孔电流列向亮：

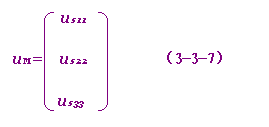
称为网孔电压源电压列向量。式（3-3-4）或（3-3-5）即为矩阵形式的网孔方程。求解式（3-3-5）即得：iM= R‾¹u_M （3-3-8）

四.支路电流与支路电压的求解
将所求得的iⅠ,iⅡ,iⅢ代入式（3-3-1），即可求得各支路电流，进一步又可根据支路的伏安关系求得各支路电压为

五.网孔法的一般步骤
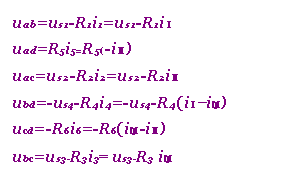
（1）.画出电路图。
（2）.设定各网孔电流的大小和参考方向，其参考方向一般都取为同一方向，即同为顺时针方向或同为逆时针方向。
（3）.对各网孔KVL约束方程，方程个数与网孔个数相等。
（4）.联立求解KVL约束方程组，即可得各网孔电流。
（5）.设定各支路电流的大小和参考方向，根据所求得的网孔电流，即可求出各支路电流和各支路电压，并进一步求出支路功率。至此，求解工作即告完毕。
例3-3-1 求图3-3-2所示电路的各支路电流和支路电压。

图3-3-2 例3-3-1的电路

解：该电路的支路数b=6,网孔数l=3。设各网孔电流的大小和参考方向如图中所示。于是可列出网孔的KVL方程为：

写成矩阵形式为

解之得：iⅠ=0.99A，iⅡ=0.61A，iⅢ=0.34A
设各支路电流的大小和参考方向如图中所示，故得：
　　i1=iⅠ=0.99A
　　i2=iⅡ-iⅠ=-0.38A
　　i3=iⅡ=0.61A
　　i4=iⅢ=0.34A
　　i5=iⅠ-iⅢ=0.65A
　　i6=iⅡ-iⅢ=0.27A
进一步可求得各支路电压为：
　　uab=10i5=6.5V
　　uad=-20i1+50=30.2V
　　uac=50i4=17V
　　ubd=-10i2+20=23.8V
　　ucd=5i3+10=13.05V
　　ubc=40i6=10.8V
当支路电流与支路电压求得后，即可很容易地求得各支路的功率。例如支路bd吸收的功率为Pbd=ubd(-i2)=23.8×0.38=9.04W,支路ad发出的功率为：Pad=uadi1=30.2×0.99=29.9W.