线性电路分析——节点法详析

一． 定义
以独立节点电位为待求变量，根据KCL对各独立节点KCL约束方程，而对电路进行分析的方法称为节点电位法，简称节点法。独立方程的个数等于独立节点的个数，即(n-1)个。非独立节点的电位取零，称为参考节点，也称"接地"，并用符号"┴" 。节点法对平面网络与立体网络均适用。 二． 独立节点电位变量的完备性与独立性
独立节点电位变量的完备性是指电路中所有的支路电压，都可由独立节点电位求得。例如图3-5-1所示电路，它有四个节点，五个支路电流。对四个节点进行编号如图中所示，并取节点(1)(2)(3)(4)为参考节点，即取节点(4)的电位φ4=0，则节点(1),(2),(3)即为独立节点。设它们的电位分别为φ1，φ2，φ3。今若φ1，φ2，φ3已知，则各支路电压即均可求得为：

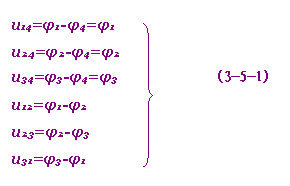
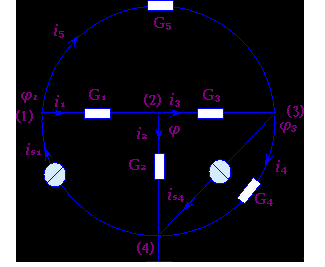
图3-5-1 节点法 可见独立节点电位变量具有完备性。
独立节点电位变量的独立性是指各独立节点电位之间不受KVL约束，彼此独立，不能互求。例如对外网孔回路，我们可KVL方程
即 　　　　　φ1-φ3+φ3-φ4+φ4-φ1=0
即　　　　　　0=0
此式恒为一等式，即不管φ2, φ3, φ4为何值都恒成立。对其它回路也能得到同样结果。所以，独立节点电位变量具有独立性。
由于独立节点电位变量具有完备性与独立性，所以可作为电路分析的变量。
三． 独立节点KCL约束方程的列写与求解
在图3-5-1所示电路中，设各支路电流的大小和参考方向如图中所示。于是对三个独立节点可列出方程：
此方程组称为独立节点电流约束方程，简称节点方程。解此方程组即可得各独立节点电位φ1，φ2，φ3。
在式（3-5-4）中，令G11=G1+G5，G22=G1+G2+G3，G33=G3+G4+G5，它们分别为节点(1)，(2)，(3)的自电导，为正值；令G12=G21=-G1，G13=G31=-G5，G23=G32=-G3;G12，G21均称为节点(1)与节点(2) 互电导，G13，G31均称为节点(1)与节点(3)的互电导，G23，G32均称为节点(2)与节点(3)的互电导。互电导为负值。令is11= is1，is22=0，is33=- is4，它们分别为流入各该节点的电流源电流的代数和，流入节点者取"+"号，流出节点者取"-"号。这样式（3-5-4）即可写为

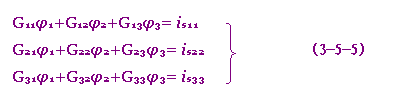
可见节点方程的列写也是很有规律的。
将上式写成矩阵形式即为：

即 GΦ=in （3-5-7）

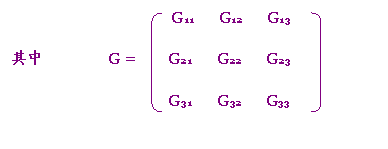
称为节点电导矩阵，为一对称阵：

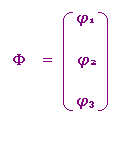
为独立节点电位列向量；

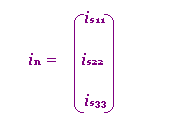
为节点电流源电流列向量。式（3-5-6）或（3-5-7）即为矩阵形式的节点方程。 求解式（3-5-7）得： Φ=G‾¹in （3-5-8）

四． 支路电压与支路电流的求解
将所求得的φ1，φ2，φ3代入式（3-5-1）即可求得各支路电压。在求支路电流时，同样应先设定它们的大小和参考方向横。若设定4各支路电流的大小和参考方向如图3-5-1中所示，则即可根据式（3-5-3）求得各支路电流。
五． 节点法的一般步骤
（1）.画出电路图。
（2）.选取参考节点，并设定各独立节点电位的大小和正负性，一般都是取各独立节点为"+"极端，参考接点为"-"极端。
（3）.对各独立节点列写KCL约束方程，方程个数与独立节点个数相等。
（4）.联立求解KCL约束方程组，即可得各独立节点电位。
（5）.设定各支路电流的大小和参考方向，根据所求得的独立节点电位，即可求得各支路电压和支路电流。至此，求解工作即告完毕。
最后要指出的是，节点法的应用极为广泛。这是因为：（1）它既适用与平面网络，也适用与非平面网络；（2）在实际电路中，其独立节点数往往要比网孔数少。
例3-5-1 列出图3-5-3（a）所示电路的节点方程并求解

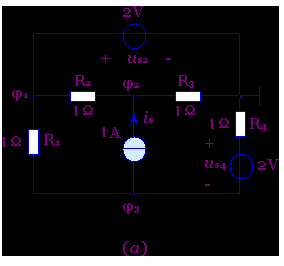
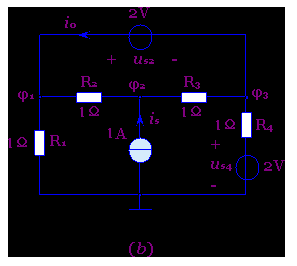
图3-5-3 例3-5-1的电路

解：该电路的特点是在其中的两个节点之间有一2V的理想电流源，无法将它等效变换为电流源。对与此种电路，若选电压源的一端（例如负端）作为参考接点，则电压源另一端的电位即为已知，即φ1=2V
这样，该电路就只有两个未知的节点电位φ2和φ3。对应的节点方程为

代入数据，联立求解以上三式即得 φ1 =2V，φ2=1.5V, φ3=0.5V.
但若选参考节点如图3-5-3(b)所示，则由于三个独立节点电位φ1，φ2，φ3均为未知，故必须对三个对立节点列出方程，且应设定流过电压源中的电流大小为i0与参考方向，如图3-5-3（b）中所示。于是可列出方程为

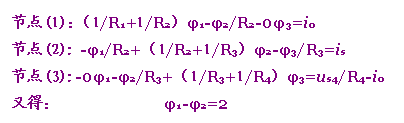
联解得 1=2.5V,φ2=2V, φ3=0.5V, i0=3A.