高速上下变频FIR滤波器的FPGA设计

滤波器的转置结构实现

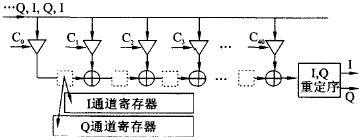
FIR 滤波器的输出是输入信号与滤波器系数的卷积求和。根据卷积表达式的计算形式, 传统上很自然地会得到滤波器的直接形式的实现结构。由于用直接形式实现的滤波器的输出延迟较大且与滤波器阶数成正比, 在硬件实现上, 一般都使用直接形式的转置结构, 如图3 所示。串行化后的I,Q 数据流, 以80MHz 速率同时馈入40 个乘法器和滤波器系数分别相乘, 所得结果作为加法器的一个输入量。加法器的另一输入量是前一个加法器在上一个时钟节拍的输出结果, 它是由图3 中小方框表示的寄存器缓存。  
　　
为了用一个滤波器硬件同时对I,Q 滤波, 设计中充分利用串行输入流的特点, 用两套寄存器( I,Q 通道寄存器, 16 b it 宽) 分别缓冲和延迟I 通道滤波的中间结果和Q 通道的中间结果, 即相当于滤波器被I 通道和Q 通道分时复用,在输出端再按序将它们分开, 输出并行的I,Q 数据流。在FPGA 的编程实现中, 乘法器采用Xilinx的N 位变量和M 位常量相乘产生M + N 位积的乘法器IP 软核。由于该软核充分利用了FPGA 查表(Look-up ) 的硬件单元结构来实现乘法, 速度较快, 一次相乘运算用时小于12 n s。  


  
滤波器的位平面结构实现
　　
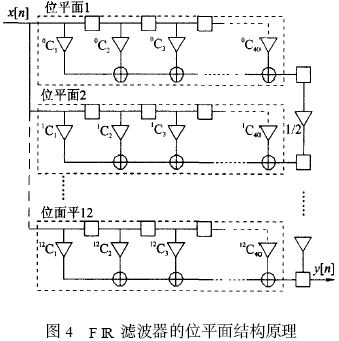
上述滤波器的转置结构是滤波器设计的传统方法。而用位平面结构快速有效地实现乘2加运算的基本思想早在86 年就被提出, 由于将其应用于滤波器设计在通用性和可重新配置性方面不如转置结构简单, 所以一直不被广泛应用。但位平面结构的高速度和高代码效率却是不容忽视的, 特别是在当今SoC 的设计实现方面。位平面结构的本质就是重新安排滤波器乘积求和运算过程的顺序。  
　　
图4 是直接形式的位平面结构原理说明, 其中每一个方框部分代表一个位平面, 分别标记为位平面1、位平面2 等。在每一个位平面内, 和输入数据相乘的仅是滤波器系数的一个b it, 位平面1 为各系数的最低位L SB, 位平面2 是各系数的最低第二位, 依此类推, 位平面12 是各系数的M SB。因为滤波器系数为12 b it 宽, 所以共有12 个位平面。输入数据同时输入到各个位平面, 所有位平面并行计算对应位的部分积及其累加结果。最后, 在每个时钟节拍下, 位平面1 输出结果右移一位(除以2) 和位平面2 输出相加, 所得结果除以2, 再和位平面3的输出相加, 这样继续相加直至最后一个位平面。由于在位平面内的乘数仅为单个b it (0 或者1) , 实质上滤波器的乘2加运算已转化为纯相加运算。  


  
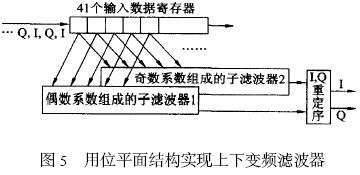
为了能够用一套滤波器同时对I,Q 数据流进行滤波, 采用图5 所示的上下变频滤波器的总体结构, 其中将整个滤波器拆分为两个子滤波器, 它们均由位平面结构实现。子滤波器1 的奇数系数设定为0, 而偶数系数不变; 子滤波器2 的偶数系数改变为0, 而奇数系数不变。输入的串行化的I,Q 数据流被40 个数据寄存器移位缓存, 两个子滤波器分别交替计算纯I 和Q 的输出值, 例如, 在某一时钟, 子滤波器1 完全忽略奇数位置上的输入数据,计算得到的是I 流的滤波结果, 与此同时, 子滤波器2 完全忽略偶数位置上的输入数据, 而计算输出Q 流的计算结果。在下一时钟计算内容与此相反:子滤波器1 计算输出Q 流结果, 而子滤波器2 计算输出I 流结果。最后由I,Q 重定序部分将这种I,Q 交织排列转换为平行输出的I,Q 流。  

  
测试结果与比较  

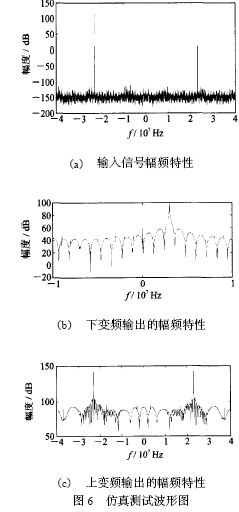
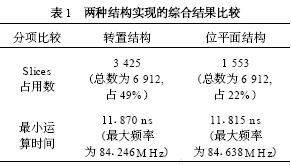
整个上下变频器被集成在一片Xilinx FPGA XCV 600HQ 24026 上, 由VHDL 设计完成, 其中滤波器分别用上述两种结构实现。图6 是设计的仿真测试结果。测试过程如下: 先用M at lab 产生如图6(a) 所示的正弦波, 作为输入文件, 测试用VHDL设计的下变频功能, 得到的下变频输出如图6 (b)所示。其中23MHz 的输入信号被下移了20MHz,且输出信号的信噪比大于50 dB; 在测试上变频功能时, 将下变频的输出信号作为VHDL 设计的输入信号, 得到上变频的输出结果如图6 (c) 所示。图中3MHz 的信号又被上移到23MHz 位置。用两种滤波器结构设计的变频器得到了几乎相同的测试结果, 最大运行速度均大于80MHz, 但它们占用芯片资源的情况却不同(见表1) , 其中逻辑资源单元(Slices) 的占用数相差一半。  


  
结束语  
用FPGA 设计实现滤波器, 采用位平面结构在芯片资源利用率方面占明显优势。这主要得益于位平面结构实现滤波器乘积2累加运算的独特方式。每一位平面计算得到的部分积通过右移一位被及时丢弃而不致影响运算精度。这就省去了一般乘法运算实现时, 为避免精度变差存储中间结果的寄存器必须留有足够的保护位。位平面结构中的运算顺序避免了大量的移位操作, 比较适合FPGA 的结构特点。如果滤波器系数中含有更多的0 bit 位, 将会减小求和操作次数, 进一步提高运算速度。相对于转置结构, 位平面结构的最大缺点是输入和输出之间有较大的延迟, 这主要是由于位平面内直接形式结构的固有延迟和各个位平面在最后输出求和过程的流水线结构所造成的, 但一般不影响实际应用。