开关电容滤波器的系统设计与实现

作者: 周 蓉

   开关电容滤波器(Switch Capitor Filter，SCF)是一种由MOS开关、电容器和运算放大器构成的离散时间模拟滤波器，实际应用中，该滤波器可与其他电路集成在同一个芯片上，通过外部端子的适当连接获得不同的响应特性。某些单独的开关电容滤波器可作为通用滤波器使用，例如自适应滤波、跟踪滤波、振动分析以及语言和音乐合成等。但运算放大器带宽、电路的寄生参数、开关与运算放大器的非理想特性以及MOS器件的噪声等都会直接影响这类滤波器的性能。开关电容滤波器的工作频率不高，其应用范围目前仅限于音频频段。但随语音／数据通信及微电子测量仪器领域内对单片集成MOSFET有源滤波器的需求剧增，促使了开关电容滤波器的研究与开发，特别是高阶SCF。因此，这里提出一种开关电容滤波器的系统设计方案。

1 开关电容滤波器的选型

1．1 类型选择

    这里所设计的开关电容滤波器是应用于电力线信号传输，传输信号频率为57．6±16、76．8±16和115．2±16 kHz，所以需要将电力线上的低频噪声(包括电力线上50 Hz的电源信号)滤除，同时还需要滤除各种不可知的高频噪声。这样带通滤波器成为最佳选择。

    滤波器的理想滤波特性是，通带内信号完全无衰减通过，阻带内信号完全衰减。但实际应用中，理想的滤波器是不存在的，只能用传输函数近似表达其滤波特性。根据对滤波器特性的不同要求，选择不同形式的近似函数，从而得到常用的滤波器：巴特沃思(Butterworth)滤波器、切比雪夫(Chebyshev)滤波器、椭圆函数(Elliptic Function)滤波器。
 
   考虑电力线通讯中的信号与噪声特性，由于电力线所接触的环境复杂，噪声源多，所以电力线上的噪声能量很高。尤其在低频部分，其噪声能量比信号能量大很多倍。这就要求滤波器有良好的带外衰减特性，而且不允许阻带部分出现纹波。因此，椭圆函数滤波器就不能满足要求，而巴特沃思滤波器的衰减特性又不够好。综合考虑，切比雪夫滤波器是最佳选择。滤波器阶数越高，其滚降速度越快，但是也意味更大的功耗和版图面积。于是这里采用6阶带通切比雪夫滤波器。

1.2 实现方式

    高阶滤波器的实现方式主要有2种：级联法和梯形法。级联法需要先得出满足频率特性要求的S域传输函数H(s)，然后经S域到Z域的频率变换后得出Z域传输函数H(x)。再将H(x)分解成一阶、二阶函数乘积，分别用一阶、二阶SC基本节实现，然后级联成整个开关电容滤波器电路。级联法实现高阶开关电容滤波器采用双线性变换法。这种方法简单明了，而且是直接级联，不存在基本节之间的反馈，只要基本节稳定，整个电路也就是稳定的。
 
    梯形法是无源梯形的有源SC模拟实现的。这种方法可进一步分为元件阻抗模拟和跳耦，前者以LC梯形滤波器为原型，用SC电路模拟原型中的阻抗元件而保持电压电荷关系不变；后者则通过用信号流程图表示LC梯形电路中的电压电流关系，然后用SC积分器实现开关电容滤波器。其中，有源跳耦结构是实现高选择性SCF的最佳选择。因为这种跳耦滤波器不仅具有通带低灵敏度特性，而且对寄生电容不敏感，因此是设计者的最佳选择。

    通过信号流程图法(SFG)，构建同相、反相、有损、无损开关电容积分器，获得梯形电路。但这种方法在LC电路原型的串臂中至少存在一个电感，而对于全极点高通SCF，不能使用这种方法，因而只能使用级联法。

2 可编程开关电容带通滤波器
 
   滤波器的编程主要是针对其频域响应进行编程，包括通带频率ω0，品质因数Q和传输函数增益的编程。其中，中心频率编程是最常用的，也是最重要的。这里设计的滤波器正是对中心频率的编程，为了得到最合理的编程二次节结构，首先应深入理解基本的二阶带通滤波器的频域响应。

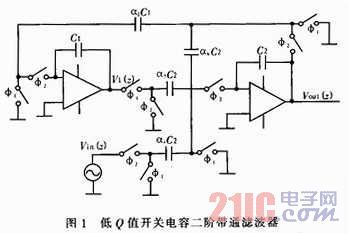
    低Q值开关电容二次节使用非常广泛，图1所示为一种常用的低Q值开关电容二阶带通滤波器(只要把所有的开关电容换算成对应的电阻，便可得到其连续时间RC的实现方式)，不难得出其Z域传输函数：


    
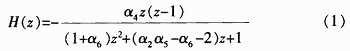
    鉴于开关电容滤波器一般都是对信号进行过采样，可以做假设ωT<<1。于是可得低Q结构的等效S域传输函数：


    
    可见，通过对α2和α5同步编程控制实现中心频率ω0的调节。在时钟频率不变的情况下，α6=ω0T／Q不变，保证ω0／Q不变，从而保证ωb和GD不变。这正是所需要的结构。然而在该设计的滤波器中，Q值并不低，可能导致α6=ω0T／Q会很小，接近于0．01，这又对电容散布带来不好的影响。
 
   于是再对高Q结构进行分析，看是否更适合本文中滤波器中心频率编程的要求。为得到良好的动态范围，选取α2=α5。