伟大的不仅仅是傅里叶是个数学公式，别的方面也伟大

义。

从数学角度解析傅里叶变换的意义

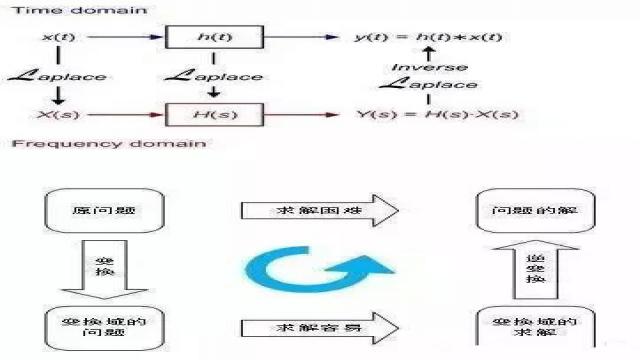
这种解决问题的思路和我们介绍的对角化时的思路是一致的。类似的还有对数变换、解析几何的坐标变换、高等代数中的线性变换；在积分中的变量代换和积分运算化简；在微分方程中所作的自变量或未知函数的变换；复变函数的保角变换。当然变换要可以逆。也就是下面介绍的核函数要可逆。

从数学的角度理解积分变换就是通过积分运算，把一个函数变成另一个函数。也可以理解成是算内积，然后就变成一个函数向另一个函数的投影：

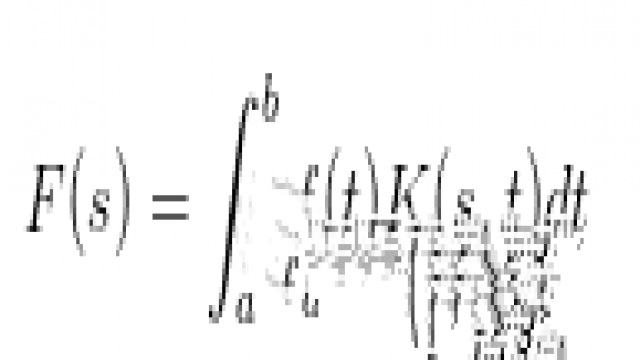
K（s，t）是积分变换的核(Kernel)。当选取不同的积分域和变换核时，就得到不同名称的积分变换。学术一点的说法是：向核空间投影，将原问题转化到核空间。所谓核空间，就是这个空间里面装的是核函数。下表列出常见的变换及其核函数：

当然，选取什么样的核主要看你面对的问题有什么特征。不同问题的特征不同，就会对应特定的核函数。把核函数作为基函数。将现在的坐标投影到核空间里面去，问题就会得到简化。之所以叫核，是因为这是最核心的地方。为什么其他变换你都没怎么听说过而只熟悉傅里叶变换和拉普拉斯变换呢？因为复指数信号才是描述这个世界的特征函数！

写到这里，我觉得早晚会有人指出我的一个问题：没有区分傅里叶级数和傅里叶变换。笔者觉得这两个概念根本没必要区分，我的理由如下：傅里叶级数和傅里叶变换的根本区别是被操作的函数是否为周期函数：当被操作函数的周期趋向于无穷大，傅里叶级数"密集"成傅里叶变换；当被操作函数的周期从无穷大变成有限值时，傅里叶变换退化成傅里叶级数。所以，其实傅里叶级数只是傅里叶变换的一种特殊情况，或者说傅里叶变换是傅里叶级数的推广。因此，笔者不希望用高深繁多的概念来把你搞晕，就没有强调二者的区别。

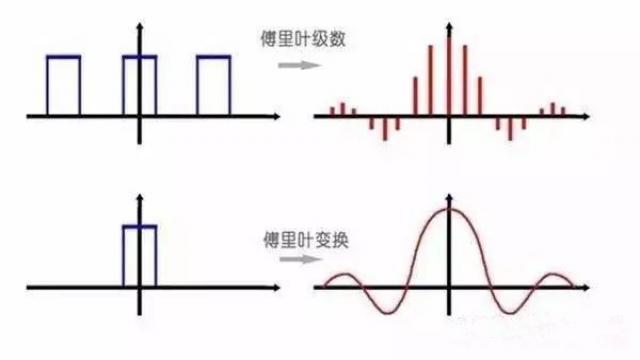
当然，这个问题还体现了时频域之间的对称(对偶)关系，而且对拉普拉斯变换也适用，请看下表：

举个例子：

比如你在时域周期延拓，那么频域就是离散的线谱；你在时域离散(采样)，那么频域就是周期的。还记得海绵宝宝和派大星那个图么？时域的窗函数在频域就是sinc函数；频域的窗函数(理想低通滤波器)在时域就是sinc函数。因此，由于非因果性，理想低通滤波器是不存在的。当然，有些公式并不严谨，只是为了形式上的好看，希望你谅解。详细而准确的推导请参考积分变换或者信号与系统类的书籍。

现代数学发现傅里叶变换具有非常好的性质，使得它如此的好用和有用，让人不得不感叹造物的神奇：

1. 傅里叶变换是线性算子，若赋予适当的范数，它还是酉算子；

    

2. 傅里叶变换的逆变换容易求出，而且形式与正变换非常类似；

    

3. 正弦基函数是微分运算的本征函数，从而使得线性微分方程的求解可以转化为常系数的代数方程的求解。在线性时不变的物理系统内，频率是个不变的性质，从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取；

    

4. 著名的卷积定理指出：傅里叶变换可以化复杂的卷积运算为简单的乘积运算，从而提供了计算卷积的一种简单手段；

    

5. 离散形式的傅里叶变换可以利用数字计算机快速的算出（其算法称为快速傅里叶变换算法（FFT)).

   
   正是由于上述的良好性质，傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。