傅里叶-->短时傅里叶变换-->小波变换的方法
从傅里叶变换到小波变换，并不是一个完全抽象的东西，完全可以讲得很形象。小波变换有着明确的物理意义，如果我们从它的提出时所面对的问题看起，可以整理出非常清晰的思路。
下面我就按照傅里叶-->短时傅里叶变换-->小波变换的顺序，讲一下为什么会出现小波这个东西、小波究竟是怎样的思路。（反正题主要求的是通俗形象，没说简短，希望不会太长不看。。）
一、傅里叶变换
关于傅里叶变换的基本概念在此我就不再赘述了，默认大家现在正处在理解了傅里叶但还没理解小波的道路上。
下面我们主要将傅里叶变换的不足。即我们知道傅里叶变化可以分析信号的频谱，那么为什么还要提出小波变换？答案就是"对非平稳过程，傅里叶变换有局限性"。看如下一个简单的信号：
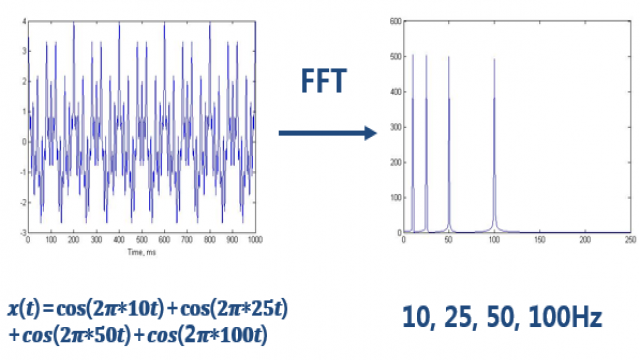
做完FFT（快速傅里叶变换）后，可以在频谱上看到清晰的四条线，信号包含四个频率成分。
一切没有问题。但是，如果是非平稳信号呢？
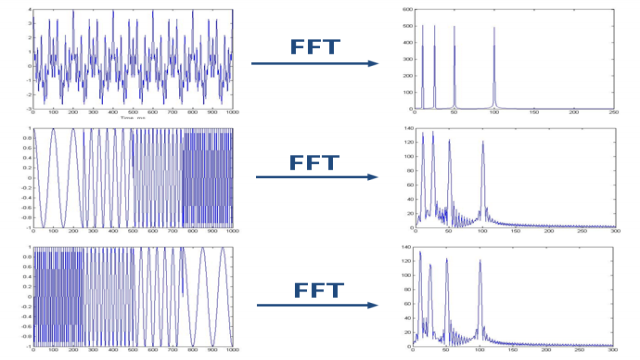
如上图，最上边的是频率始终不变的平稳信号。而下边两个则是频率随着时间改变的非平稳信号，它们同样包含和最上信号相同频率的四个成分。
做FFT后，我们发现这三个时域上有巨大差异的信号，频谱却非常一致。尤其是下边两个非平稳信号，我们从频域上无法区分它们，因为它们包含的四个频率的信号的成分确实是一样的，只是出现的先后顺序不同。
可见，傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分，但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号，可能频谱图一样。
然而平稳信号大多是人为制造出来的，自然界的大量信号几乎都是非平稳的，所以在比如生物医学信号分析等领域的papers中，基本看不到单纯傅里叶变换这样naive的方法。
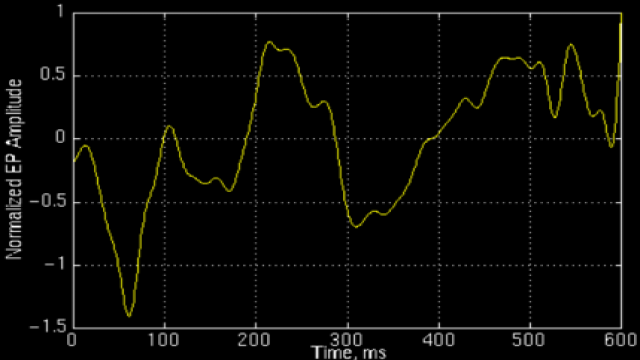
上图所示的是一个正常人的事件相关电位。对于这样的非平稳信号，只知道包含哪些频率成分是不够的，我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况，各个时刻的瞬时频率及其幅值——这也就是时频分析。
二、短时傅里叶变换（Short-time Fourier Transform, STFT）
一个简单可行的方法就是——加窗。我又要套用方沁园同学的描述了，"把整个时域过程分解成无数个等长的小过程，每个小过程近似平稳，再傅里叶变换，就知道在哪个时间点上出现了什么频率了。"这就是短时傅里叶变换。
看图：
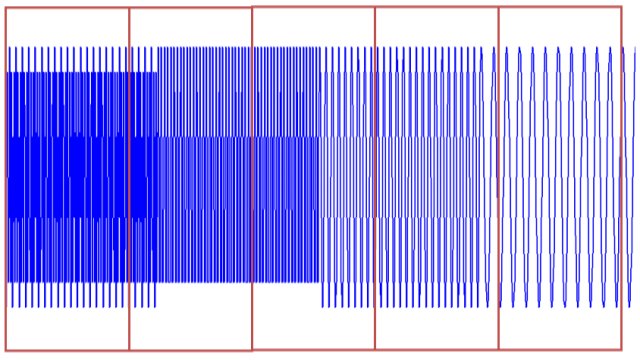
时域上分成一段一段做FFT，不就知道频率成分随着时间的变化情况了吗！
用这样的方法，可以得到一个信号的时频图了：
图上既能看到300Hz, 200 Hz, 100 Hz, 50 Hz四个频域成分，还能看到出现的时间。两排峰是对称的，所以大家只用看一排就行了。
是不是棒棒的？时频分析结果到手。但是STFT依然有缺陷。
使用STFT存在一个问题，我们应该用多宽的窗函数？
窗太宽太窄都有问题：
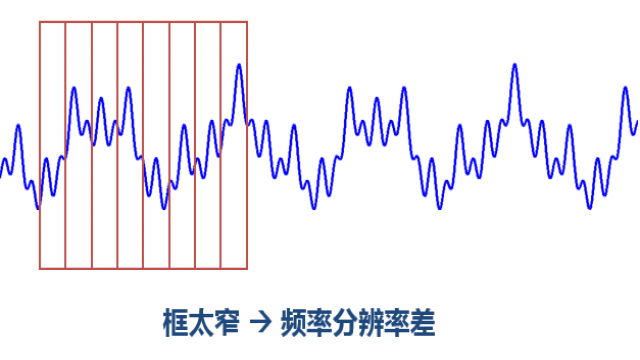
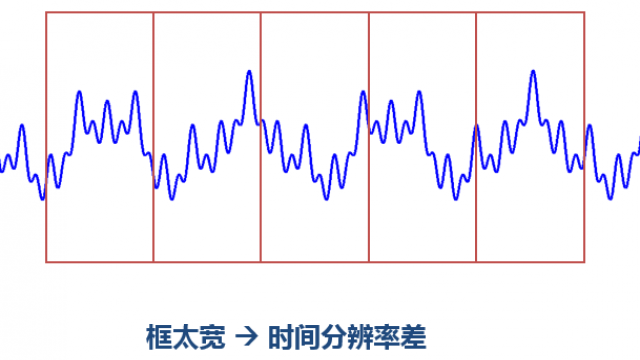
窗太窄，窗内的信号太短，会导致频率分析不够精准，频率分辨率差。窗太宽，时域上又不够精细，时间分辨率低。
（这 里插一句，这个道理可以用海森堡不确定性原理来解释。类似于我们不能同时获取一个粒子的动量和位置，我们也不能同时获取信号绝对精准的时刻和频率。这也是 一对不可兼得的矛盾体。我们不知道在某个瞬间哪个频率分量存在，我们知道的只能是在一个时间段内某个频带的分量存在。 所以绝对意义的瞬时频率是不存在的。）
看看实例效果吧：
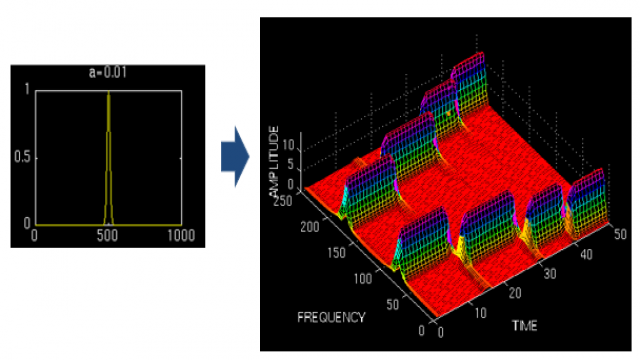
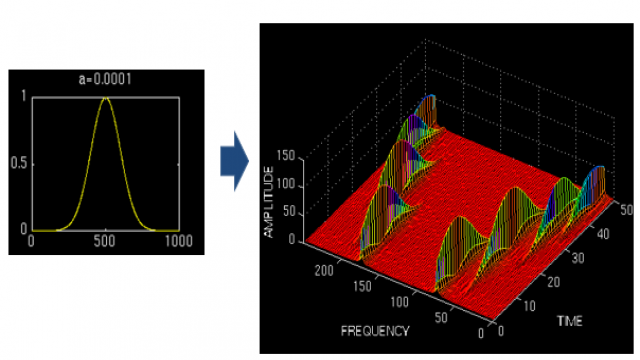
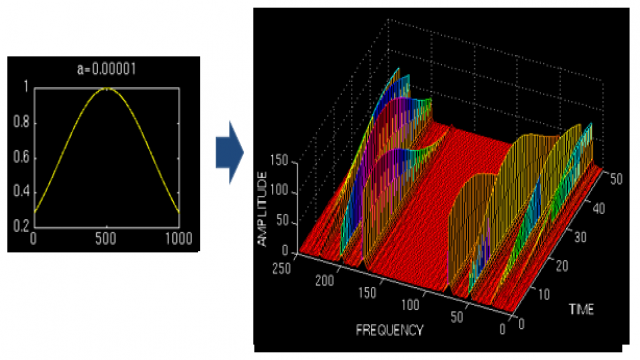
上图对同一个信号（4个频率成分）采用不同宽度的窗做STFT，结果如右图。用窄窗，时频图在时间轴上分辨率很高，几个峰基本成矩形，而用宽窗则变成了绵延的矮山。但是频率轴上，窄窗明显不如下边两个宽窗精确。
所以窄窗口时间分辨率高、频率分辨率低，宽窗口时间分辨率低、频率分辨率高。对于时变的非稳态信号，高频适合小窗口，低频适合大窗口。然而STFT的窗口是固定的，在一次STFT中宽度不会变化，所以STFT还是无法满足非稳态信号变化的频率的需求。
三、小波变换
那么你可能会想到，让窗口大小变起来，多做几次STFT不就可以了吗？！没错，小波变换就有着这样的思路。
但事实上小波并不是这么做的（关于这一点，方沁园同学的表述"小波变换就是根据算法，加不等长的窗，对每一小部分进行傅里叶变换"就不准确了。小波变换并没有采用窗的思想，更没有做傅里叶变换。）
至于为什么不采用可变窗的STFT呢，我认为是因为这样做冗余会太严重，STFT做不到正交化，这也是它的一大缺陷。
于是小波变换的出发点和STFT还是不同的。STFT是给信号加窗，分段做FFT；而小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率，还可以定位到时间了~
【解释】
来我们再回顾一下傅里叶变换吧，没弄清傅里叶变换为什么能得到信号各个频率成分的同学也可以再借我的图理解一下。
傅里叶变换把无限长的三角函数作为基函数：
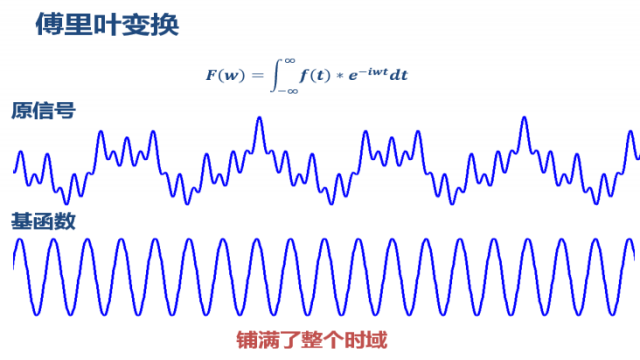
这 个基函数会伸缩、会平移（其实是两个正交基的分解）。缩得窄，对应高频；伸得宽，对应低频。然后这个基函数不断和信号做相乘。某一个尺度（宽窄）下乘出来 的结果，就可以理解成信号所包含的当前尺度对应频率成分有多少。于是，基函数会在某些尺度下，与信号相乘得到一个很大的值，因为此时二者有一种重合关系。 那么我们就知道信号包含多少该频率的成分。
- 傅里叶变换，拉普拉斯变换，泰勒展开及Z变换有什么意义(07-05)
- 伟大的不仅仅是傅里叶是个数学公式，别的方面也伟大(07-07)
- 快速傅里叶变换与多项式乘法有什么关系(07-22)
- 谐波分析方法一览(09-08)
- 傅里叶变换拉普拉斯变换的物理解释及区别(07-14)
- 妤傛ḿ楠囩亸鍕暥瀹搞儳鈻肩敮鍫濆悋閹存劕鐓跨拋顓熸殌缁嬪顨滅憗锟�
閸忋劍鏌熸担宥咁劅娑旂姴鐨犳０鎴滅瑩娑撴氨鐓＄拠鍡礉閹绘劕宕岄惍鏂垮絺瀹搞儰缍旈懗钘夊閿涘苯濮幃銊ユ彥闁喐鍨氶梹澶歌礋娴兼ḿ顫呴惃鍕殸妫版垵浼愮粙瀣瑎...
- 娑擃厾楠囩亸鍕暥瀹搞儳鈻肩敮鍫濆悋閹存劕鐓跨拋顓熸殌缁嬪顨滅憗锟�
缁箖鈧拷30婢舵岸妫亸鍕暥閸╃顔勭拠鍓р柤閿涘奔绗撶€硅埖宸跨拠鎾呯礉閸斺晛顒熼崨妯烘彥闁喕鎻崚棰佺娑擃亜鎮庨弽鐓庣殸妫版垵浼愮粙瀣瑎閻ㄥ嫯顩﹀Ч锟�...
- Agilent ADS 閺佹瑥顒熼崺纭咁唲鐠囧墽鈻兼總妤勵棅
娑撴挸顔嶉幒鍫ｎ嚦閿涘苯鍙忛棃銏ｎ唹鐟欘枃DS閸氬嫮顫掗崝鐔诲厴閸滃苯浼愮粙瀣安閻㈩煉绱遍崝鈺傚亶閻€劍娓堕惌顓犳畱閺冨爼妫跨€涳缚绱癆DS...
- HFSS鐎涳缚绡勯崺纭咁唲鐠囧墽鈻兼總妤勵棅
鐠у嫭绻佹稉鎾愁啀閹哄牐顕抽敍灞藉弿闂堛垼顔夐幒鍦欶SS閻ㄥ嫬濮涢懗钘夋嫲鎼存梻鏁ら敍灞藉簻閸斺晜鍋嶉崗銊╂桨缁崵绮洪崷鏉款劅娑旂姵甯夐幓顡嶧SS...
- CST瀵邦喗灏濆銉ょ稊鐎广倕鐓跨拋顓熸殌缁嬪顨滅憗锟�
閺夊孩妲戝ú瀣╁瘜鐠佽绱濋崗銊╂桨鐠佸弶宸緾ST閸氬嫰銆嶉崝鐔诲厴閸滃苯浼愮粙瀣安閻㈩煉绱濋崝鈺傚亶韫囶偊鈧喕鍤滅€涳附甯夐幓顡塖T鐠佹崘顓告惔鏃傛暏...
- 鐏忓嫰顣堕崺铏诡攨閸╃顔勭拠鍓р柤
娑撳洣绗€妤傛ɑ銈奸獮鍐叉勾鐠у嚖绱濇潻娆庣昂鐠囧墽鈻兼稉杞扮稑閸︺劌鐨犳０鎴炲Η閺堫垶顣崺鐔枫亣鐏炴洘瀚甸懘姘剧礉閹垫挷绗呴崸姘杽閻ㄥ嫪绗撴稉姘唨绾偓...
- 瀵邦喗灏濈亸鍕暥濞村鍣洪幙宥勭稊閸╃顔勭拠鍓р柤閸氬牓娉�
鐠愵厺鎷遍崥鍫ユ肠閺囨潙鐤勯幆鐙呯礉缂冩垵鍨庨妴渚€顣剁拫鍙樺崕閵嗕胶銇氬▔銏犳珤閵嗕椒淇婇崣閿嬬爱閿涘本鍨滅憰浣圭壉閺嶉绨块柅锟�...
