伟大的不仅仅是傅里叶是个数学公式，别的方面也伟大

写在最前，这是摘自《神奇的矩阵第二季》爱上积分变换那一节。

傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是，傅里叶分析的公式看起来太复杂了，所以很多大一新生上来就懵圈并从此对它深恶痛绝。老实说，这么有意思的东西居然成了大学里的杀手课程，不得不归咎于编教材的人实在是太严肃了。所以我一直想写一个有意思的文章来解释傅里叶分析，有可能的话高中生都能看懂的那种。所以，不管读到这里的您从事何种工作，我保证您都能看懂，并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友，也希望不要看到会的地方就急忙往后翻，仔细读一定会有新的发现。

有关傅里叶

傅里叶是一位法国数学家和物理学家的名字，英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣，于1807年在法国科学学会上发表了一篇论文，运用正弦曲线来描述温度分布，论文里有个在当时具有争议性的决断：任何连续周期信号可以由一组适当的正弦曲线组合而成。

当时审查这个论文的人，其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827)，当拉普拉斯和其它审查者投票通过并要发表这个论文时，拉格朗日坚决反对，在他此后生命的六年中，拉格朗日坚持认为傅里叶的方法无法表示带有棱角的信号，如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望，拒绝了傅里叶的工作，幸运的是，傅里叶还有其它事情可忙，他参加了政治运动，随拿破仑远征埃及，法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。

拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号。

但是，我们可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别，基于此，傅里叶是对的。

话是这么说没错，可是二者总要存在差异，甚至在跳变沿处，傅里叶逼近会产生Gibbs现象，我们为什么还要进行傅里叶展开或傅里叶变换呢？

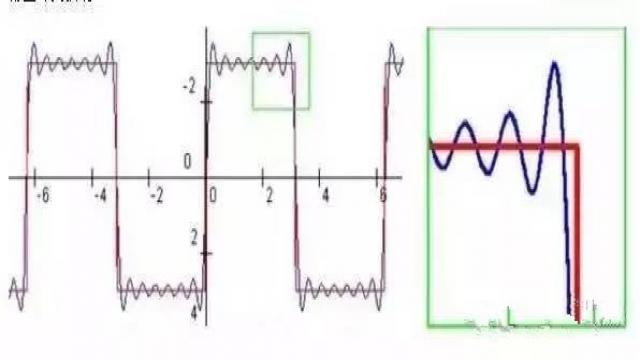
为什么要傅里叶展开和变换？

首先，我们从物理系统的特征信号角度来解释。

我们知道，大自然中很多现象可以抽象成一个线性时不变系统来研究，无论你用微分方程还是传递函数或者状态空间描述。

线性时不变系统可以这样理解：

输入输出信号满足线性关系，而且系统参数不随时间变换。对于大自然界的很多系统，一个正弦曲线信号输入后，输出的仍是正弦曲线，只有幅度和相位可能发生变化，但是频率和波的形状仍是一样的。

也就是说正弦信号是系统的特征向量！当然，指数信号也是系统的特征向量，表示能量的衰减或积聚。自然界的衰减或者扩散现象大多是指数形式的，或者既有波动又有指数衰减（复指数形式），因此具有特征的基函数就由三角函数变成复指数函数。但是，如果输入是方波、三角波或者其他什么波形，那输出就不一定是什么样子了。所以，除了指数信号和正弦信号以外的其他波形都不是特征信号。

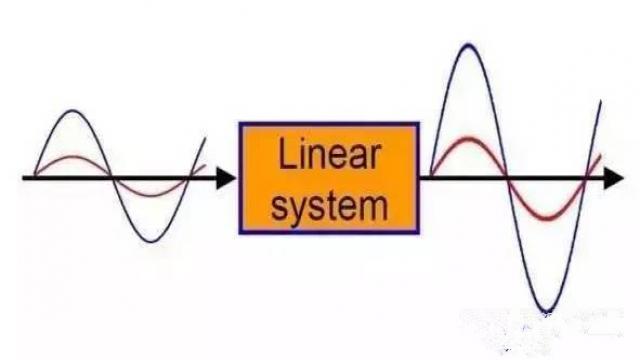
怎么理解我所说的特征向量和特征信号这个名字呢？其实这来源于线性代数：我们知道矩阵A作用一个特征向量x可以用数学语言这样描述：，那么系统作用一个特征信号用数学语言描述就是。形式结构相同，只是一个是有限长度的向量，另一个是无限长度的信号而已。既然是特征向量，我们就想能不能用特征向量来表示自然界的信号和一个物理系统呢？这样做的好处就是知道输入，我们就能很简单那的写出输出。我们来看一个实际的例子，击弦乐器——钢琴。琴键被小锤敲击后，产生声音，见下图。

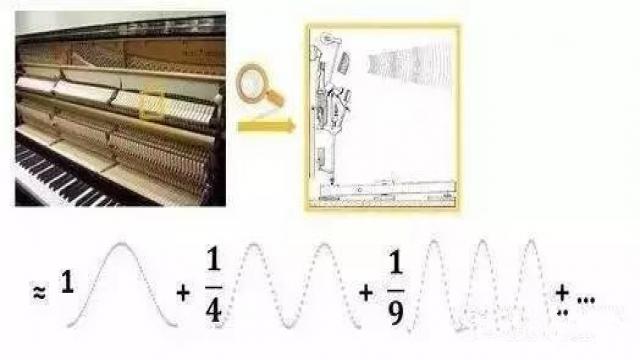
你可以认为声音是琴键随时间变化的，也可以看成是各种波的叠加。用数学的表达式就是这个样子的：

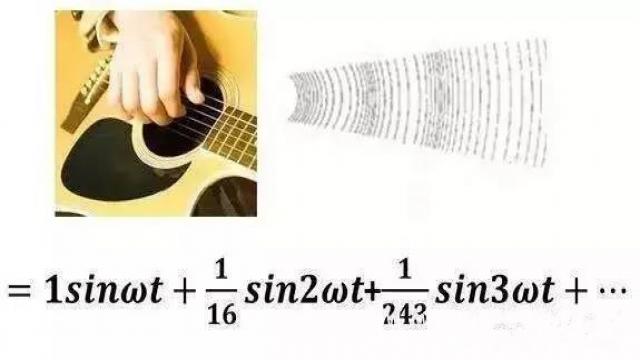
凡有变化的波(交流、频率)才能传递信号，一个一直不变的直流信号是无法传递信息的。这种"交流"是指广义的，普遍的，无论是自然界里蝙蝠探路，人们互相交谈，还是卫星接收信号，都属于交流的范畴。

为了传递信号，产生交流，我们需要以"波"作为信号的载体。最简单的波，就以一定频率传播。蝙蝠发出了超声波，人们说话，声带振动带动了空气疏密波（声波），卫星识别电磁波。这样，我们就有了频率的概念。更进一步，除了手机GHz的波这些经典电磁波，在量子世界里，原子的跃迁也是以一定的频率发生的。我们甚至可以说，自然选择了以这些单频的模式为基矗对于一个信号来说，信号强度随时间的变化规律就