一种模／数混合型FIR噪声滤波器设计

摘要：针对现有数字FIR噪声滤除技术的噪声放大问题，结合模拟电路的方法，提出一种新的混合型FIR噪声滤波技术。该方法采用电荷泵将锁相环中数字控制的相位误差转换为模拟域电荷，调制器的输出经过一个寄存器链实现一个或数个时钟周期的延时，从中选出若干抽头分别去控制对应的分频器或相位选择器，从而量化所产生的经过各支路鉴相器的瞬时相位误差，在一个多输入电荷泵中合成为模拟域误差电荷，通过提供恒定单位直流增益，解决现有数字FIR噪声滤除技术的噪声放大问题，这种新型的滤波器具有如下特点：离散时间域工作，模拟失配不敏感，有助于提高线性度，额外硬件开销小。
关键词：FIR滤波；△-∑调制；锁相环；量化噪声

0 引言
一般的相位反馈系统中使用锁相环通过分频器的比例关系，可以输出一个频率是输入参考信号N倍的时钟。由于传统结构的分频比只能是整数限制，使得频率分辨率直接取决于输入信号频率。△-∑分数锁相环通过采用数字调制，实现了分数分频比，从而可以提供更高精度的频率分辨率，这为时钟信号的产生和频率规划带来更大的灵活性。然而，△-∑调制器的使用也引入了量化噪声，在低过采样率的环路中限制了带外相位噪声性能，需要加以解决。现有的量化噪声抑制技术仍然需要较大的硬件代价，并设法减小失配等非理想因素才能得到比较好的性能。由此可见，数字FIR噪声滤除技术具有结构简单，可靠性高的优点，但存在噪声增益问题。目前针对这一问题还投有很好的解决办法，本文结合模拟和数字实现各自的优点，设计出一种混合型FIR噪声滤波技术，该技术能有效地解决上述问题。

1 电路设计原理
混合型FIR噪声滤除电路的结构设计如图1所示。在△-∑锁相环或△-∑延时锁定环中，鉴相器输入端的2个信号之间存在受调制器控制的瞬时相位误差，电荷泵将这个数字控制的相位误差转换为模拟域电荷。为了实现对量化噪声的FIR滤波功能，结构中采用了多个鉴相器并联的形式。△-∑调制器的输出并不像传统结构中直接去控制分频器或相位选择器实现量化操作，而是经过一个寄存器链实现一个或数个时钟周期的延时，并从中选出若干抽头分别去控制对应的分频器或相位选择器，量化所产生的瞬时相位误差经过各支路鉴相器后在一个多输入电荷泵中合成为模拟域误差电荷。

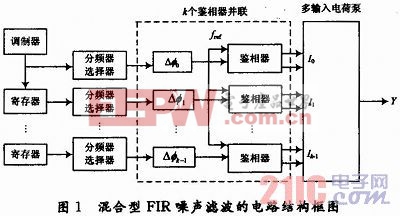
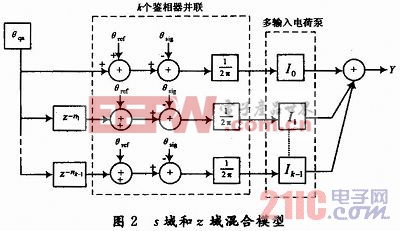
该结构对应的S域和Z域混合模型如图2所示。经过推导可以得到电荷泵的输出为：

式中：θref为参考信号相位；θsig为环路返回信号相位；θqn为相位域的量化噪声；ni为调制器输出的延时深度，Ii为多输入电荷泵的各支路电流；fref为鉴相器工作频率；H(z)为针对量化噪声的等效FIR滤波的传递函数：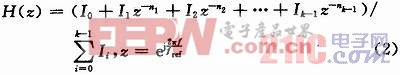

电荷泵电流在该结构中扮演了双重角色。从式(1)可以看出，同常规结构一样，总电流影响了环路动态特性；另一方面，式(2)表明各支路电流决定了所实现FIR滤波器传递函数的各项系数。只要根据所要实现的传递函数设置调制器输出的延时深度以及电荷泵各支路电流的分配比例，就可以实现全定制的噪声整形。此外，式(2)中当f=0时，将有H(z)≡1。这表明无论设计参数如何选取，该结构所实现的FIR滤波器恒有单位直流增益，因此从根本上解决了现有数字FIR噪声滤除技术中的噪声增益问题。

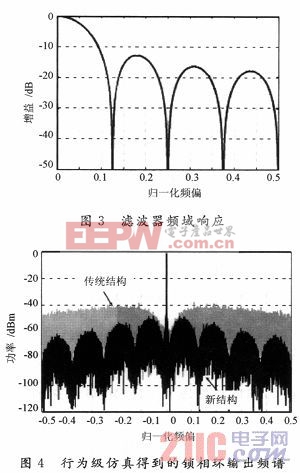
现以8抽头混合型FIR滤波器为例，分析该结构所实现的全定制噪声整形。通过采用并行8支路鉴相器和1个8输入的电荷泵，并给电荷泵各支路分配相同的电流，设置图1中调制器输出的每级延迟为单个时钟周期，可以实现如图3所示的滤波器频域响应。对应的传递函数为：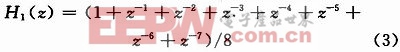

图4是行为级仿真得到的采用混合型FIR滤波器的新结构锁相环输出的频谱，并与传统结构做了对比。所有模块均为无噪声理想模型，因此频谱中只含△-∑调制带来的量化噪声。所用参考时钟频率为14．318 MHz；输出频率为532 MHz，对应的分频比为37．156；电荷泵总电流为320μA，对应每个支路40μA；振荡器增益为250 MHz／V；环路滤波器采用2阶；环路带宽设为700 kHz，对应的过采样率仅为10；所用调制器为3阶MASH结构。图中横坐标按照参考时钟频率归一化。对比图4和图3可以看出，混合型FIR滤波器按照其传递函数实现了预期的对量化噪声的抑制。

图5(a)是行为级仿真得到的环路建立过程中振荡器控制电压的瞬态波形。从相同的建立过程(包括其中的周期滑动现象)可以看出，由于新结构中多输入电荷泵的总电流与传统结构保持一致，因此混合型FIR滤波器的使用不会影响环路动态特性。
图5(b)是对比采用混合型FIR滤波器的新结构与传统结构在环路锁定时的瞬时相位误差电压(即2阶环路滤波器中电阻两端的电压)。从中可以看到，尽管环路呈现相同的动态特性，但新结构中的瞬时相位误差电压远小于传统结构。这表明高频量化噪声得到了混合型FIR滤波器的有效抑制。

2 失配的影响
相比现有数字FIR噪声滤除技术，所提出的混合型FIR滤波在实现过程中引入了模拟域的操作，因此需要考虑失配的影响。由于最终噪声滤除效果是用滤波器传递函数来描述的，所以失配的影响因素同样也可以归结到对滤波器传递函数的改变，主要包括以下3个方面：
(1)电荷泵各支路电流的失配△Ii改变了传递函数的系数；
(2)延时失配引起调制器输出延时深度改变△ni；
(3)并行支路间非同步引入附加相位偏移△φi。
考虑到这些因素后，式(2)所示的FIR滤波器传递函数将转变为：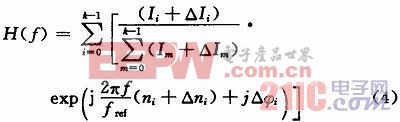

其中，作为模拟模块的电荷泵，电流镜失配引起的各支路电流的改变是不可避免的，因此是影响FIR滤波器传递系数的主要因素。通过在上电初始化时对并行各支路加以同步复位后影响因素(3)，将与影响因素(2)一样，由于相关的电路模块为寄存器链、分频器以及鉴频鉴相器等离散时间域工作的数字模块，因此主要受时钟抖动影响，从而相对△Ii而言，△ni和△φi可以忽略。
基于以上考虑，假设电流失配、延时失配以及非同步引起的附加相差分别满足3σ=15％，3σ=1％和3σ=0．01π的正态分布。对由式(3)给出的混合型FIR滤波器的频域响应做Monte-Carlo分析，可以得到如图6所示的结果。