全面掌控频域
时间:07-01
来源:互联网
点击:
基于FPGA的实现方式
上文介绍的DFT和IDFT的实现一般采用嵌套循环,每个循环完成N次计算。因此实现DFT计算所需的时间为:
DFTtime = N * N * Kd ft
其中,Kdft表示完成每次迭代的处理时间。显然这种方法实现起来极为耗时。为此FPGA中实现DFT一般使用快速傅里叶变换算法(FFT)。FFT常常被称为我们时代最重要的算法,因为它对许多行业都产生根本性的影响。
FFT与DFT算法稍有不同,它计算的是复数DFT,即它需要实时域信号和虚时域信号,得到的结果的宽度是n位而非n/2位。这意味着如果需要计算实DFT,必须首先把虚部设为0,然后把时域信号转移到实部。如果要在赛灵思FPGA实现FFT,可以有两种选择。您可以使用您选择的HDL重新编写FFT,也可以使用Vivado®设计套件IP Catalog或其他来源提供的FFT IP。除非有不得已的原因不能使用IP,为缩短开发时间,一般都应该选择IP。
FFT的基本方法是将时域信号分解为一系列单点时域信号。因为样本被重新排序,这个过程常被称为位反转。如果没有位反转算法这一捷径可走,那么创建单点时域信号的级数可以用Log2 N计算得到,其中,N表示位数。
随后使用这些单点时域信号计算每个点的频谱。这一计算相当简单,因为频谱与单点的时域相等。
这些单频点的重组是FFT算法最复杂环节。必须每一级重组一次这些频点,恰好是时域分解的反向操作。因此要重建频谱需要Log2 N级,这里就是著名的蝶形FFT发挥作用的地方。
与DFT的执行时间相比,FFT用时为:
FFTtime = K f ft * N Log2 N
与计算DFT相比,执行时间明显缩短。
在FPGA中实现FFT算法时,还必须考虑FFT采样数。FFT采样数将决定本底噪声,在此之下将无法再看到有用信号。FFT采样数还将决定频点之间的间距。使用下面的公式可以确定FFT采样数:
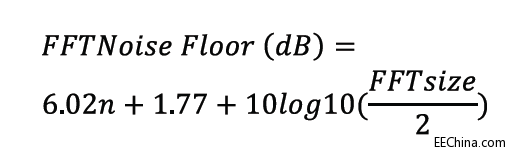
其中,n为时域中量化位的数量,FFTSize为FFT采样数。对基于FPGA的设计,这一般是2的幂,如256、512、1,024等。频点可采用下列公式计算出其等间隔:
举个非常简单的例子,在采样频率(FS)为100 MHz的情况下,使用128个FFT样本可实现0.39 Hz的频率精度。这意味着如果频率彼此之间的间隔小于0.39 Hz将无法分辨。
高速采样
许多FPGA中的FFT应用和较高性能的系统都工作在非常高的频率下。高频运行会产生自己特有的设计难题。
因为在高频下无法维持奈奎斯特采样率(每个周期两个样本),因此需要不同的方法。例如使用2.5 GHz采样率采样3 GHz全功率带宽模拟输入。运用奈奎斯特频率法则,高于1.25 GHz的信号将被混叠到有用的第一个奈奎斯特域中。这些混叠镜像将成为基本信号的谐波分量,因此包含与非混叠信号相同的信息,如图2所示。

图2 - 奈奎斯特域与混叠
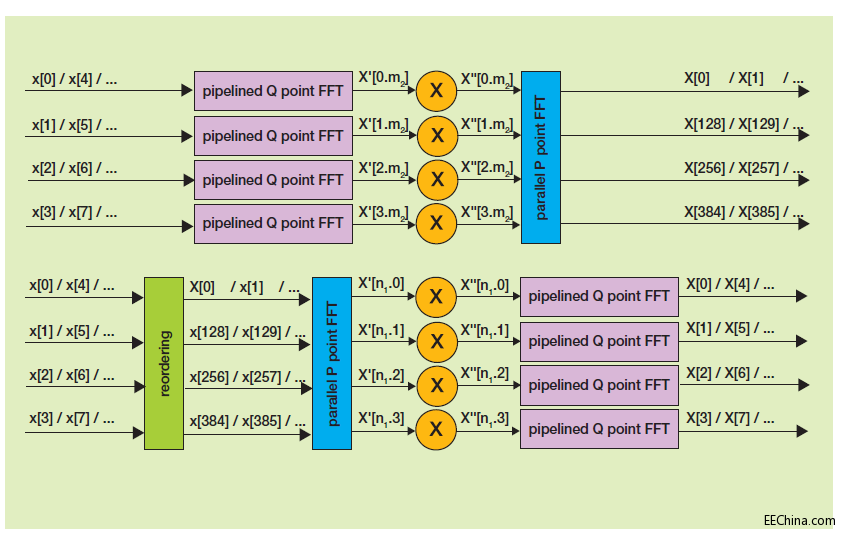
图3 - 分解与重组FFT结构
要判断得到的谐波或谐波成分的频率布局,可使用下列算法:
Fharm = N × Ffund
IF (Fharm = Odd Nyquist Zone)
Floc = Fharm Mod Ffund
Else
Floc = Ffund-(Fharm Mod Ffund)
End
其中,N表示有用谐波的整数。
继续前述例子,如果采样率为2,500 MHz,基频为1,807 MHz,则会在第一奈奎斯特域中产生693 MHz的谐波成分,供在FFT中进一步处理。
在掌握了频谱的基本知识之后,下一个需要考虑的关键因素是如何将这些ADC和DAC器件与FPGA连接在一起。在上面所述的实例中,,无法从ADC接收频率为采样频率一半(采样率为2.5 Gbps)的数据。为此,高性能数据转换器使用多路复用的数字输入输出,该输入输出工作在较低频率下,一般为转换器的采样频率的四分之一或二分之一(即FS/4或 FS/2)。
FPGA通过多个数据流接收到数据后,如果希望执行DFT,那么下一个要解决的问题就是如何在FPGA内处理数据。包括电信和射电天文在内的多种应用常用的方法是使用重组或分解FFT结构(如图3所示)。
虽然这种应用与直接FFT相比更复杂,使用这种方法能够实现高速处理。
正您所见,在频域中工作并非像最初想象的那样困难,特别是有IP模块帮助转入转出频域的情况下。此外还有多种方法可供选择,帮助您实现高速处理。
上文介绍的DFT和IDFT的实现一般采用嵌套循环,每个循环完成N次计算。因此实现DFT计算所需的时间为:
DFTtime = N * N * Kd ft
其中,Kdft表示完成每次迭代的处理时间。显然这种方法实现起来极为耗时。为此FPGA中实现DFT一般使用快速傅里叶变换算法(FFT)。FFT常常被称为我们时代最重要的算法,因为它对许多行业都产生根本性的影响。
FFT与DFT算法稍有不同,它计算的是复数DFT,即它需要实时域信号和虚时域信号,得到的结果的宽度是n位而非n/2位。这意味着如果需要计算实DFT,必须首先把虚部设为0,然后把时域信号转移到实部。如果要在赛灵思FPGA实现FFT,可以有两种选择。您可以使用您选择的HDL重新编写FFT,也可以使用Vivado®设计套件IP Catalog或其他来源提供的FFT IP。除非有不得已的原因不能使用IP,为缩短开发时间,一般都应该选择IP。
FFT的基本方法是将时域信号分解为一系列单点时域信号。因为样本被重新排序,这个过程常被称为位反转。如果没有位反转算法这一捷径可走,那么创建单点时域信号的级数可以用Log2 N计算得到,其中,N表示位数。
随后使用这些单点时域信号计算每个点的频谱。这一计算相当简单,因为频谱与单点的时域相等。
这些单频点的重组是FFT算法最复杂环节。必须每一级重组一次这些频点,恰好是时域分解的反向操作。因此要重建频谱需要Log2 N级,这里就是著名的蝶形FFT发挥作用的地方。
与DFT的执行时间相比,FFT用时为:
FFTtime = K f ft * N Log2 N
与计算DFT相比,执行时间明显缩短。
在FPGA中实现FFT算法时,还必须考虑FFT采样数。FFT采样数将决定本底噪声,在此之下将无法再看到有用信号。FFT采样数还将决定频点之间的间距。使用下面的公式可以确定FFT采样数:
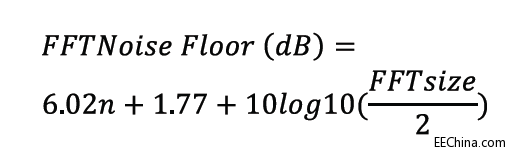
其中,n为时域中量化位的数量,FFTSize为FFT采样数。对基于FPGA的设计,这一般是2的幂,如256、512、1,024等。频点可采用下列公式计算出其等间隔:
举个非常简单的例子,在采样频率(FS)为100 MHz的情况下,使用128个FFT样本可实现0.39 Hz的频率精度。这意味着如果频率彼此之间的间隔小于0.39 Hz将无法分辨。
高速采样
许多FPGA中的FFT应用和较高性能的系统都工作在非常高的频率下。高频运行会产生自己特有的设计难题。
因为在高频下无法维持奈奎斯特采样率(每个周期两个样本),因此需要不同的方法。例如使用2.5 GHz采样率采样3 GHz全功率带宽模拟输入。运用奈奎斯特频率法则,高于1.25 GHz的信号将被混叠到有用的第一个奈奎斯特域中。这些混叠镜像将成为基本信号的谐波分量,因此包含与非混叠信号相同的信息,如图2所示。

图2 - 奈奎斯特域与混叠

图3 - 分解与重组FFT结构
要判断得到的谐波或谐波成分的频率布局,可使用下列算法:
Fharm = N × Ffund
IF (Fharm = Odd Nyquist Zone)
Floc = Fharm Mod Ffund
Else
Floc = Ffund-(Fharm Mod Ffund)
End
其中,N表示有用谐波的整数。
继续前述例子,如果采样率为2,500 MHz,基频为1,807 MHz,则会在第一奈奎斯特域中产生693 MHz的谐波成分,供在FFT中进一步处理。
在掌握了频谱的基本知识之后,下一个需要考虑的关键因素是如何将这些ADC和DAC器件与FPGA连接在一起。在上面所述的实例中,,无法从ADC接收频率为采样频率一半(采样率为2.5 Gbps)的数据。为此,高性能数据转换器使用多路复用的数字输入输出,该输入输出工作在较低频率下,一般为转换器的采样频率的四分之一或二分之一(即FS/4或 FS/2)。
FPGA通过多个数据流接收到数据后,如果希望执行DFT,那么下一个要解决的问题就是如何在FPGA内处理数据。包括电信和射电天文在内的多种应用常用的方法是使用重组或分解FFT结构(如图3所示)。
虽然这种应用与直接FFT相比更复杂,使用这种方法能够实现高速处理。
正您所见,在频域中工作并非像最初想象的那样困难,特别是有IP模块帮助转入转出频域的情况下。此外还有多种方法可供选择,帮助您实现高速处理。
FPGA 赛灵思 电子 电压 电流 传感器 示波器 频谱分析仪 ADC 滤波器 DAC 相关文章:
- 基于FPGA的片上系统的无线保密通信终端(02-16)
- 基于Virtex-5 FPGA设计Gbps无线通信基站(05-12)
- 基于FPGA的DVI/HDMI接口实现(05-13)
- 基于ARM的嵌入式系统中从串配置FPGA的实现(06-09)
- 采用EEPROM对大容量FPGA芯片数据实现串行加载(03-18)
- 赛灵思:可编程逻辑不仅已是大势所趋,而且势不可挡(07-24)
