全面掌控频域
时间:07-01
来源:互联网
点击:
手把手课堂:FPGA 101 全面掌控频域
作者:
Adam P. Taylor
e2v公司首席工程师
aptaylor@theiet.org
许多应用都要求能够在频域内开展工作。本文将介绍如何处理FPGA设计中的频域问题。
对许多工程师而言,在频域中开展工作不如在时域中开展工作那么自然,可能是因为频率与复杂的数学运算有关。但是要充分发挥赛灵思FPGA解决方案的潜力,您需要在这两个域中自由切换。
令人欣慰的是详细地掌握频域并不像您最初想象的那样令人生畏。不管是您自己设计的定制模块还是市场上现有的IP模块,都能帮助您轻松转入转出频域。同时在频域中实现高速处理的方法也不乏其数。
时域还是频域?
工程师既能在时域中检验和处理信号,根据时间分析信号,也能在频域中检验和处理信号,根据频率分析信号。项目对工程师的主要要求之一,就是应该知道什么时候应该开展哪种分析。
一般在电子系统中,需要考查的信号是一个不断变化的电压、电流或频率。它可以是传感器的输出,也可能是系统其他部分生成的输出。在时域中,您可以测量信号的幅度、频率和周期,以及信号上升或下降时间等更有意义的参数。实验室环境中观察时域信号常用的是示波器或逻辑分析仪。
但是信号的一些参数体现在频域内。必须在频率中分析这些参数,才能解读其中包含的信息。在频域中可以识别信号的频率分量、各自的幅度和每种频率的相位。由于在频域中便于开展卷积运算,因此在频域中工作也能大大简化信号处理。卷积是一种将两种信号混合成第三种信号的数学方法。和时域分析一样,如果想要在实验室环境中观察频域信号,可以使用频谱分析仪。
根据信号的类型,如重复性还是非重复性、离散还是非离散,有多种方法可用于时域和频域之间的变换
对某些应用而言在时域中工作比较合适,例如用于监测更大型系统的电压或温度的系统。虽然噪声可能是个问题,在许多情况下取一定数量样本的平均值就可以满足要求。但对其他应用来说,最好是在频域中开展工作。例如需要从另一信号中过滤某种信号的信号处理应用,或是需要将信号与噪声源分离的信号处理应用,最好在频率中开展分析。
由于采样是在时域中完成的,在时域中工作基本不需要对量化数字信号进行后处理。与此相反,在频域中开展工作首先要求应用将量化数据从时域变换到频域。同样,从频域输出后处理过的数据时,需要从频率转回到时域。
如何进行变换?
根据信号的类型,如重复性还是非重复性、离散还是非离散,有多种方法可用于时域和频域之间的变换,包括傅里叶级数、傅里叶变换和Z变换。尤其是在电子信号处理和FPGA应用中,最常用到的变换是离散傅里叶变换(DFT),傅里叶变换中的一种。工程师使用DFT分析具有周期性和离散性的信号,即由一定数量均匀分布在采样频率中的n位样本组成的信号。在许多应用中这种信号一般来自系统内的ADC。
简单地说,DFT的工作原理就是把输入信号分解成代表信号正弦分量和余弦分量的两个输出信号。因此对由N个样本组成的时域序列,DFT会返回两组N/2+1个余弦波样本和正弦波样本,分别被称为实分量和虚分量(图1)。实样本和虚样本的宽度为n位输入信号宽度的n/2。
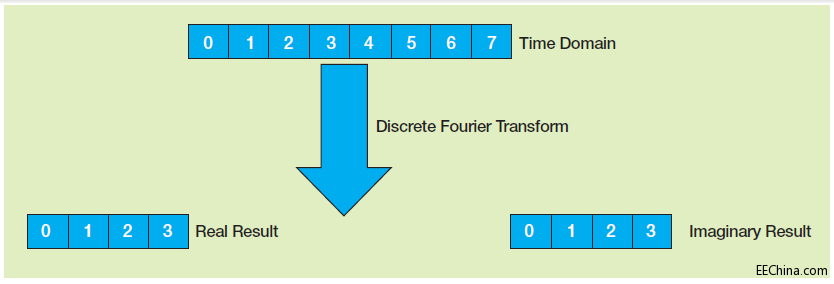
图1 - 时域中的n位被变换为频域中n/2实位和n/2虚位
计算DFT的算法十分简明,如下式所示:
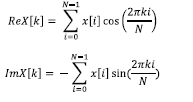
其中,x{i}代表时域信号;i的取值为0到N-1;k的取值为0到N/2。这种方法被称为关联法,其功能是将输入信号与对应迭代的正弦波或余弦波相乘,以确定其幅度。
当然,您可能想要在应用中的某点从频域变换回时域。为此可以使用综合公式,它将实波形和虚波形结合起来,重建时域信号,即:
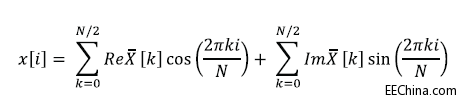
但ReX和ImX是正弦波和余弦波的缩放结果,因此需要进行缩放。除Rex[0]和Rex[N/2]之外的所有情况,ReX和ImX的值均为ReX[k]或ImX[k]除以N/2。对Rex[0]和Rex[N/2],则除以N。出于明显的理由,这种运算被称为傅里叶反变换(IDFT)。
通过探讨确定DFT和IDFT所使用的算法,可能有助于了解如何加以利用这些算法。
您可以使用Octave、MATLAB®乃至Excel对所采集的数据进行DFT计算。许多实验室工具,如示波器,也能根据需要执行DFT计算。
不过需要指出的是上述的DFT和IDFT被称为实DFT和实IDFT,因为输入的是实数而非复数。很快就会清楚为何要了解这一点。
需要进行变换的地方
从电信到图像处理、雷达和声纳,难以想象有比傅里叶变换更强大、更适合并可实现FPGA中的分析技术。实际上DFT是最常用FPGA应用之一(即,生产有限输入响应(FIR)滤波器系数)的基础(参阅赛灵思中国通讯第43期《数字滤波器设计与实现详情》)。
但其用途不局限于滤波。DFT和IDFT还可用于电信处理中,用于执行电信通道的信道化和重组。在频谱监测应用中,它们可用来判断监测带宽内的频率构成。在图像处理中,它们用于处理图像卷积,供滤波器内核开展图像模式识别等操作。所有这些应用在实现过程中一般使用比上文介绍的更有效的算法来计算DFT。
总而言之,了解DFT并将其实现在FPGA中是每个FPGA开发人员的必备技能。
作者:
Adam P. Taylor
e2v公司首席工程师
aptaylor@theiet.org
许多应用都要求能够在频域内开展工作。本文将介绍如何处理FPGA设计中的频域问题。
对许多工程师而言,在频域中开展工作不如在时域中开展工作那么自然,可能是因为频率与复杂的数学运算有关。但是要充分发挥赛灵思FPGA解决方案的潜力,您需要在这两个域中自由切换。
令人欣慰的是详细地掌握频域并不像您最初想象的那样令人生畏。不管是您自己设计的定制模块还是市场上现有的IP模块,都能帮助您轻松转入转出频域。同时在频域中实现高速处理的方法也不乏其数。
时域还是频域?
工程师既能在时域中检验和处理信号,根据时间分析信号,也能在频域中检验和处理信号,根据频率分析信号。项目对工程师的主要要求之一,就是应该知道什么时候应该开展哪种分析。
一般在电子系统中,需要考查的信号是一个不断变化的电压、电流或频率。它可以是传感器的输出,也可能是系统其他部分生成的输出。在时域中,您可以测量信号的幅度、频率和周期,以及信号上升或下降时间等更有意义的参数。实验室环境中观察时域信号常用的是示波器或逻辑分析仪。
但是信号的一些参数体现在频域内。必须在频率中分析这些参数,才能解读其中包含的信息。在频域中可以识别信号的频率分量、各自的幅度和每种频率的相位。由于在频域中便于开展卷积运算,因此在频域中工作也能大大简化信号处理。卷积是一种将两种信号混合成第三种信号的数学方法。和时域分析一样,如果想要在实验室环境中观察频域信号,可以使用频谱分析仪。
根据信号的类型,如重复性还是非重复性、离散还是非离散,有多种方法可用于时域和频域之间的变换
对某些应用而言在时域中工作比较合适,例如用于监测更大型系统的电压或温度的系统。虽然噪声可能是个问题,在许多情况下取一定数量样本的平均值就可以满足要求。但对其他应用来说,最好是在频域中开展工作。例如需要从另一信号中过滤某种信号的信号处理应用,或是需要将信号与噪声源分离的信号处理应用,最好在频率中开展分析。
由于采样是在时域中完成的,在时域中工作基本不需要对量化数字信号进行后处理。与此相反,在频域中开展工作首先要求应用将量化数据从时域变换到频域。同样,从频域输出后处理过的数据时,需要从频率转回到时域。
如何进行变换?
根据信号的类型,如重复性还是非重复性、离散还是非离散,有多种方法可用于时域和频域之间的变换,包括傅里叶级数、傅里叶变换和Z变换。尤其是在电子信号处理和FPGA应用中,最常用到的变换是离散傅里叶变换(DFT),傅里叶变换中的一种。工程师使用DFT分析具有周期性和离散性的信号,即由一定数量均匀分布在采样频率中的n位样本组成的信号。在许多应用中这种信号一般来自系统内的ADC。
简单地说,DFT的工作原理就是把输入信号分解成代表信号正弦分量和余弦分量的两个输出信号。因此对由N个样本组成的时域序列,DFT会返回两组N/2+1个余弦波样本和正弦波样本,分别被称为实分量和虚分量(图1)。实样本和虚样本的宽度为n位输入信号宽度的n/2。

图1 - 时域中的n位被变换为频域中n/2实位和n/2虚位
计算DFT的算法十分简明,如下式所示:
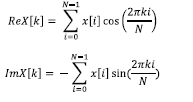
其中,x{i}代表时域信号;i的取值为0到N-1;k的取值为0到N/2。这种方法被称为关联法,其功能是将输入信号与对应迭代的正弦波或余弦波相乘,以确定其幅度。
当然,您可能想要在应用中的某点从频域变换回时域。为此可以使用综合公式,它将实波形和虚波形结合起来,重建时域信号,即:
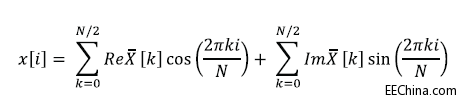
但ReX和ImX是正弦波和余弦波的缩放结果,因此需要进行缩放。除Rex[0]和Rex[N/2]之外的所有情况,ReX和ImX的值均为ReX[k]或ImX[k]除以N/2。对Rex[0]和Rex[N/2],则除以N。出于明显的理由,这种运算被称为傅里叶反变换(IDFT)。
通过探讨确定DFT和IDFT所使用的算法,可能有助于了解如何加以利用这些算法。
您可以使用Octave、MATLAB®乃至Excel对所采集的数据进行DFT计算。许多实验室工具,如示波器,也能根据需要执行DFT计算。
不过需要指出的是上述的DFT和IDFT被称为实DFT和实IDFT,因为输入的是实数而非复数。很快就会清楚为何要了解这一点。
需要进行变换的地方
从电信到图像处理、雷达和声纳,难以想象有比傅里叶变换更强大、更适合并可实现FPGA中的分析技术。实际上DFT是最常用FPGA应用之一(即,生产有限输入响应(FIR)滤波器系数)的基础(参阅赛灵思中国通讯第43期《数字滤波器设计与实现详情》)。
但其用途不局限于滤波。DFT和IDFT还可用于电信处理中,用于执行电信通道的信道化和重组。在频谱监测应用中,它们可用来判断监测带宽内的频率构成。在图像处理中,它们用于处理图像卷积,供滤波器内核开展图像模式识别等操作。所有这些应用在实现过程中一般使用比上文介绍的更有效的算法来计算DFT。
总而言之,了解DFT并将其实现在FPGA中是每个FPGA开发人员的必备技能。
FPGA 赛灵思 电子 电压 电流 传感器 示波器 频谱分析仪 ADC 滤波器 DAC 相关文章:
- 基于FPGA的片上系统的无线保密通信终端(02-16)
- 基于Virtex-5 FPGA设计Gbps无线通信基站(05-12)
- 基于FPGA的DVI/HDMI接口实现(05-13)
- 基于ARM的嵌入式系统中从串配置FPGA的实现(06-09)
- 采用EEPROM对大容量FPGA芯片数据实现串行加载(03-18)
- 赛灵思:可编程逻辑不仅已是大势所趋,而且势不可挡(07-24)
