基于Verilog硬件描述语言的AES密码算法实现
时间:12-28
来源:互联网
点击:
2.3.2 ShiftRows()和InvShiftRows()的设计
行移位变换作用在中间态的行上,将状态中的行按不同的偏移量进行循环移位。加密运算中间态的0~3行,分别向右循环移动O,1,2,3个字节。该操作仅是将数据按字节进行移动,硬件实现时只需在布线上进行调整,基本不占硬件资源。
解密过程只是行移位的逆变换,即分别向左循环移动0,1,2,3个字节。同样,该操作也仅将数据按字节移动。如果有字节的位置改变,只需在布线上进行修改。
2.3.3 MixColumns()和InvMixColumns()的设计
MixColumns()变换以矩阵中的列为单位,将每列看作一个GF(28)域上的四阶多项式,将多项式乘以c(x)/d(x)并对x4+1取模。其中c(x)为:
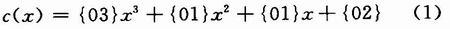
在相应的解密过程中:
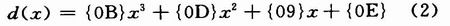
同样对
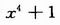
取模。
为了降低整个模块的复杂度,考虑将加解密运算中列混合变换的部分电路进行复用,对比加解密运算所乘的多项式,可以发现{03}x可以用
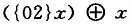
表示,同理:
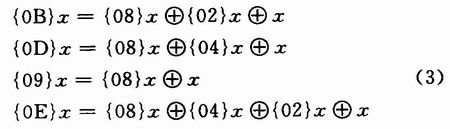
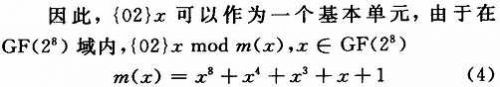
这样:
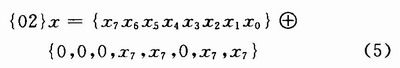
由于
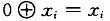
,式(8)只需要4个异或门就可实现。将该单元记为xtime()函数。其硬件结构如图2所示。加密时所取的系数较小{01,02,03},所以只需经过一次xtime()单元,便将乘法运算转换为移位操作和加法运算的复合。
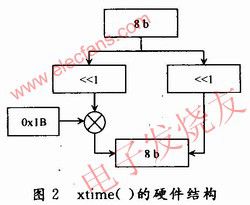
而解密时,Mixcolumns()的系数是{09,OB,OE,OD),实现这些乘法显然比加密时需要更多的时间。由式(3)可知,InvMixcolumns()也可用xtime()函数与异或门实现。这样,就可以实现加/解密列混合变换电路的复用,从而节约电路面积,提高解密运算速度。
2.3.4 密钥加AddRoundKey()的设计
在AES算法中,加法用异或操作实现。密钥加是中间状态的每一字节按位与轮密钥进行异或操作,加法的逆运算也用异或操作,所以可采用逐位异或操作实现加解密运算的AddRoundkey()。AddRoundkey()的逆运算是其自身。因此本文在常规轮中把加密时的密钥加、列混合变换和解密时的密钥加、列混合变换集成为同一模块,通过加解密信号的选择,实现加解密运算的列变换和密钥加功能。这样可消除加解密硬件结构的差异,同时也可降低轮密钥处理的复杂度。
2.4 密钥扩展模块的设计
轮密钥的产生是AES加解密运算的基础,密钥扩展模块的作用就是产生除了初始密钥本身之外的10个轮密钥,分别用于10轮加解密运算。
加密运算采用密钥内部扩展的方式,即加密运算与密钥扩展并行完成。这一过程,每一轮变换都要和相应密钥扩展轮次生成的子密钥进行异或,因此需使用状态机控制加密运算和密钥扩展的同步,否则会发生混乱。需要指出,使用内部扩展方式可以提高整个加密运算速度。而解密运算采用外部扩展方式,即密钥扩展完之后再进行解密运算,因为解密运算使用的初始密钥是密钥扩展生成的最后一轮子密钥。
3 仿真测试与结果
根据前述设计思路和优化措施,系统采用Mentor公司专门为各逻辑器件制造厂商设计的第三方专用仿真工具ModelSim 6.o进行功能仿真,给出了最后的功能仿真图。
3.1 加密运算的仿真测试
一次完整的加密操作,需要12个时钟周期。其中,10个周期用于10个轮循环变换,1个时钟周期用于初始的密钥扩展,1个时钟周期用于密文的输出。加密运算的功能测试仿真波形如图3所示。
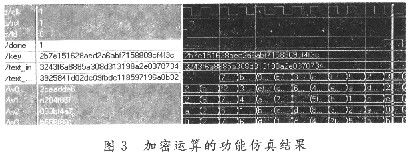
从图3给出的加密运算功能仿真结果可以看出,加密运算与密钥扩展过程是并行进行。当“rst”变为低电平,“ld”变为高电平时,明文3243f6a8885a308d313198a2e0370734与密钥2b7el5l628aed2a6abf7158809cf4f3c分别同时加载到加解密运算模块与密钥扩展模块中;在下一个时钟周期,密钥扩展模块生成1轮子密钥,等待加密轮变换中的密钥加操作。当完成1次加密过程后,“done”信号变为高电平,同时输出密文3925841d02dc09fbdc118597196a0632。从图3中同时也可以看出,密钥扩展模块总是提前一个时钟周期生成下一轮的子密钥,这样可以保证密钥扩展与加密运算同时进行而不会发生错乱,并且还可提高加密速度,节约资源占用和减少面积。使用DC进行综合和优化后,加密运算模块面积不超过20 000个等效门,其中组合逻辑面积为14 264门,非组合逻辑面积为3 878门。
3.2 解密运算的仿真测试
在解密过程中,完成一次解密操作同样需要12时钟周期。其中,10个周期用于10个轮循环变换,1个时钟周期用于初始密钥的加载,1个时钟周期用于密文的输出。在解密过程中,本文采用在解密之前所生成的10轮子密钥,因为解密初始需要的子密钥是密钥扩展得到的最后一轮子密钥,而最后一轮需要的子密钥是密钥扩展的初始密钥。如图4所示。

解密过程与密钥扩展过程不是同步的,当“kld”为高电平时,从第1个时钟周期开始,便将初始密钥2b7e151628aed2a6abf7158809cf4f-3c输入到密钥扩展模块中,之后经过10个时钟周期生成10轮子密钥,并存储到寄存器中。当“ld”为高电平时,密文3925841d02dc09fbdcll-8597196a0632开始加载到解密模块中,经过10个时钟周期将解密的密文输出,同时“done”信号变为高电平,表示解密过程结束,并输出明文3243f6a8885a308d313198a2e0370734。
对比图3与图4仿真测试结果可知,加解密运算的功能正确,即解密运算能够正确地解出加密运算的密文。解密运算模块使用DC进行综合和优化后面积不超过25 000个等效门。其中组合逻辑面积为10 495门,非组合逻辑面积为14 142门。由于密钥扩展与解密过程不是同步进行,占用了寄存器存储解密过程所需的10轮子密钥,所以非组合逻辑面积比加密运算模块大。但需要指出,由于加/解密运算模块部分电路采用复用的方法实现,所以整个加/解密运算模块的实际总面积比没有复用时减小。
行移位变换作用在中间态的行上,将状态中的行按不同的偏移量进行循环移位。加密运算中间态的0~3行,分别向右循环移动O,1,2,3个字节。该操作仅是将数据按字节进行移动,硬件实现时只需在布线上进行调整,基本不占硬件资源。
解密过程只是行移位的逆变换,即分别向左循环移动0,1,2,3个字节。同样,该操作也仅将数据按字节移动。如果有字节的位置改变,只需在布线上进行修改。
2.3.3 MixColumns()和InvMixColumns()的设计
MixColumns()变换以矩阵中的列为单位,将每列看作一个GF(28)域上的四阶多项式,将多项式乘以c(x)/d(x)并对x4+1取模。其中c(x)为:
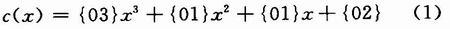
在相应的解密过程中:
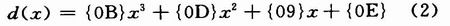
同样对
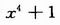
取模。
为了降低整个模块的复杂度,考虑将加解密运算中列混合变换的部分电路进行复用,对比加解密运算所乘的多项式,可以发现{03}x可以用
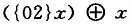
表示,同理:
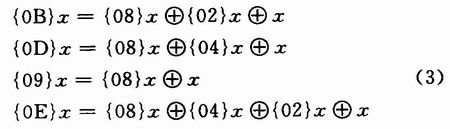
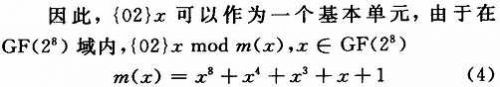
这样:
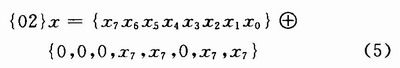
由于
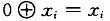
,式(8)只需要4个异或门就可实现。将该单元记为xtime()函数。其硬件结构如图2所示。加密时所取的系数较小{01,02,03},所以只需经过一次xtime()单元,便将乘法运算转换为移位操作和加法运算的复合。

而解密时,Mixcolumns()的系数是{09,OB,OE,OD),实现这些乘法显然比加密时需要更多的时间。由式(3)可知,InvMixcolumns()也可用xtime()函数与异或门实现。这样,就可以实现加/解密列混合变换电路的复用,从而节约电路面积,提高解密运算速度。
2.3.4 密钥加AddRoundKey()的设计
在AES算法中,加法用异或操作实现。密钥加是中间状态的每一字节按位与轮密钥进行异或操作,加法的逆运算也用异或操作,所以可采用逐位异或操作实现加解密运算的AddRoundkey()。AddRoundkey()的逆运算是其自身。因此本文在常规轮中把加密时的密钥加、列混合变换和解密时的密钥加、列混合变换集成为同一模块,通过加解密信号的选择,实现加解密运算的列变换和密钥加功能。这样可消除加解密硬件结构的差异,同时也可降低轮密钥处理的复杂度。
2.4 密钥扩展模块的设计
轮密钥的产生是AES加解密运算的基础,密钥扩展模块的作用就是产生除了初始密钥本身之外的10个轮密钥,分别用于10轮加解密运算。
加密运算采用密钥内部扩展的方式,即加密运算与密钥扩展并行完成。这一过程,每一轮变换都要和相应密钥扩展轮次生成的子密钥进行异或,因此需使用状态机控制加密运算和密钥扩展的同步,否则会发生混乱。需要指出,使用内部扩展方式可以提高整个加密运算速度。而解密运算采用外部扩展方式,即密钥扩展完之后再进行解密运算,因为解密运算使用的初始密钥是密钥扩展生成的最后一轮子密钥。
3 仿真测试与结果
根据前述设计思路和优化措施,系统采用Mentor公司专门为各逻辑器件制造厂商设计的第三方专用仿真工具ModelSim 6.o进行功能仿真,给出了最后的功能仿真图。
3.1 加密运算的仿真测试
一次完整的加密操作,需要12个时钟周期。其中,10个周期用于10个轮循环变换,1个时钟周期用于初始的密钥扩展,1个时钟周期用于密文的输出。加密运算的功能测试仿真波形如图3所示。

从图3给出的加密运算功能仿真结果可以看出,加密运算与密钥扩展过程是并行进行。当“rst”变为低电平,“ld”变为高电平时,明文3243f6a8885a308d313198a2e0370734与密钥2b7el5l628aed2a6abf7158809cf4f3c分别同时加载到加解密运算模块与密钥扩展模块中;在下一个时钟周期,密钥扩展模块生成1轮子密钥,等待加密轮变换中的密钥加操作。当完成1次加密过程后,“done”信号变为高电平,同时输出密文3925841d02dc09fbdc118597196a0632。从图3中同时也可以看出,密钥扩展模块总是提前一个时钟周期生成下一轮的子密钥,这样可以保证密钥扩展与加密运算同时进行而不会发生错乱,并且还可提高加密速度,节约资源占用和减少面积。使用DC进行综合和优化后,加密运算模块面积不超过20 000个等效门,其中组合逻辑面积为14 264门,非组合逻辑面积为3 878门。
3.2 解密运算的仿真测试
在解密过程中,完成一次解密操作同样需要12时钟周期。其中,10个周期用于10个轮循环变换,1个时钟周期用于初始密钥的加载,1个时钟周期用于密文的输出。在解密过程中,本文采用在解密之前所生成的10轮子密钥,因为解密初始需要的子密钥是密钥扩展得到的最后一轮子密钥,而最后一轮需要的子密钥是密钥扩展的初始密钥。如图4所示。

解密过程与密钥扩展过程不是同步的,当“kld”为高电平时,从第1个时钟周期开始,便将初始密钥2b7e151628aed2a6abf7158809cf4f-3c输入到密钥扩展模块中,之后经过10个时钟周期生成10轮子密钥,并存储到寄存器中。当“ld”为高电平时,密文3925841d02dc09fbdcll-8597196a0632开始加载到解密模块中,经过10个时钟周期将解密的密文输出,同时“done”信号变为高电平,表示解密过程结束,并输出明文3243f6a8885a308d313198a2e0370734。
对比图3与图4仿真测试结果可知,加解密运算的功能正确,即解密运算能够正确地解出加密运算的密文。解密运算模块使用DC进行综合和优化后面积不超过25 000个等效门。其中组合逻辑面积为10 495门,非组合逻辑面积为14 142门。由于密钥扩展与解密过程不是同步进行,占用了寄存器存储解密过程所需的10轮子密钥,所以非组合逻辑面积比加密运算模块大。但需要指出,由于加/解密运算模块部分电路采用复用的方法实现,所以整个加/解密运算模块的实际总面积比没有复用时减小。
集成电路 电路 RFID 仿真 Mentor ModelSim Verilog 相关文章:
- 周立功:如何兼顾学习ARM与FPGA(05-23)
- 初学者如何学习FPGA(08-06)
- 为何、如何学习FPGA(05-23)
- FPGA 重复配置和测试的实现(08-14)
- 适用于消费性市场的nano FPGA技术(09-27)
- 赛灵思“授之以渔”理论:危机中如何巧降成本(06-04)
