基于FPGA的电力线载波调制系统的研究
时间:11-08
来源:互联网
点击:
电力线载波(PLC)通信作为电力系统特有的通信方式,广泛用于电力系统的调度通信、生产指挥、行政业务通信以及其他各种信息的传输。随着数字通信技术的发展,采用电力线上网、进行多媒体通信也具有宽阔的前景,电力线载波通信已经成为当今研究热点之一。
线路调制单元是电力线载波机中关键部件之一。为了提高频带的利用率,线路调制一般采用单边带调制方式。使用数字化处理方法来实现线路的单边带调制,能够克服模拟电路的诸多缺陷。线路调制需要完成正交变换、滤波和频谱搬移等处理,运算量与采样率直接相关。高采样率导致了高的运算量,低成本DSP芯片无法满足运算需求。FPGA可用于实现DSP运算处理单元,达到实时完成数字信号处理功能的目的,它为线路调制单元的数字化实现提供了一条性价比较高的途径。本文将介绍线路调制的FPGA实现,包括:线路调制单元数字化实现的总体设计,CIC和FIR滤波器的FPGA实现以及载波发生器单元的设计。
线路调制解调实现方案
电力线载波通信标准要求的信号频率为40~500kHz,频带宽度为4kHz。根据奈奎斯特定理,采样频率不能小于1MHz。采用数字化处理方式实现调制就是将信号的频谱搬移过程转化为数字域的数值计算过程。单边带信号可以表示为x(n)cos(wn)±x^(n)sin(wn),式中x(n)为基带信号,x^(n)为基带信号的正交信号,w为载波频率。由该式可知,完成单边带调制需要信号的正交变换、载波信号的产生、信号与载波的乘加等数值运算。希尔伯特变换是一种便于采用FPGA实现的正交变换方法,它可由系数具有奇对称特性的FIR滤波器实现。
基带信号的频率较低,相应应以较低的采样率采样,而调制信号的频率较高,应以较高的采样率采样。因此在调制过程中必须进行采样率的提升,内插技术可以实现采样率的变换。调制单元调制部分的数字化实现的逻辑结构如图1所示。

由图1可见,调制单元由正交变换、内插和调制三部分组成。完成正交变换的Hilbert滤波器为系数奇对称的FIR滤波器,延迟保持了正交信号与原始信号的时间同步。载波发生器,乘法器和加法器完成单边带调制。载波发生器由查表法实现,地址为13位,字长为16位,可以产生所需要的各种载波频率。内插完成采样率的提升,再用低通滤波器滤除无用频率分量。在设计中,通过内插将信号采样率由8kS/s提升至8.192MS/s,内插率I=1024。分两级完成:第一级内插率I=8,该级内插采用128阶系数偶对称FIR滤波器滤波。第二级内插率I=128,该级内插采用3级级联的CIC(积分梳状)滤波器。
由上述方案可见,合理设计FIR、CIC滤波器和载波发生器电路是线路调制单元数字化实现的关键,线路调制单元和其他的组件进行数据交换,控制和接口电路在此不作一一赘述。
滤波器的FPGA设计
线路调制解调需要用到FIR和CIC两种滤波器,这两种滤波器的共同特点是,具有线性相位,非常适合应用需求。但这两种滤波器对FPGA资源耗费较大,因此必须采用合理的结构减少FPGA资源的开销。
1 CIC滤波器的设计
设计CIC滤波器时,首先要考虑滤波器的增益,防止溢出。内插均选用三级级联的CIC滤波器,传递函数为H(z)=((1-z-128)/(1-z-1))3。由传递函数可以求出滤波器的增益为1283,增加的字长为log2(128)3=21位,输入信号宽度为13位,实现时必须预留21+13=34位防止溢出。将内插器与滤波器结合起来并对其实现如图2所示。

图2 cic内插
程序设计采用VHDL语言,用Quartus II 3.0综合后CIC滤波器耗费资源350个LE(Logic Element)。根据Hogenaur的剪除理论在每一级输出时都可以剪除掉最后的若干位。通过信噪比的计算,可确定剪除位数,设计中积分部分每级可以剪除6位,分别取22、28和34位,梳状部分每级剪除1位,分别取14、15和16位,滤波器的输出为13位。采用剪除理论后,消耗的资源为240个LE,资源消耗减少了32%。
2 FIR滤波器的设计
FIR滤波器阶数高,如果按其级联结构实现时资源的利用率非常低,须加以改进。一种方法是提高时钟速度,重复利用乘法器和加法器。这种方法程序设计比较复杂,时钟提升也导致功耗增加,额外资源的消耗较多。另一种方法是利用FIR滤波器的分布式结构进行设计,这是一种高效的方法。信号x(n)通过N抽头,n位的FIR滤波器可以用下式表示,其中h(n)是滤波器系数,y为输出信号。
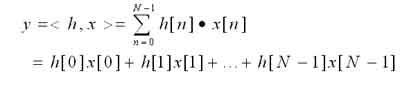
输入信号x(n)采用补码的形式,可表示为

重新对上式求和如下:
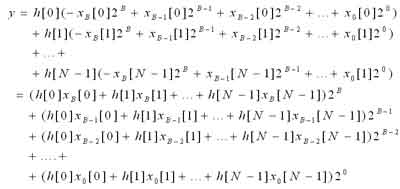
简写形式如下:
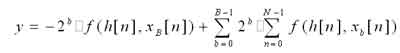
由上式可看出,把输入信号每位的值xb作为地址,将滤波器系数h(n)的值和xb的每一位xb(n)乘积叠加,并将结果存入ROM中,就可以通过查表并移位相加而得到最终内积的结果。整个滤波器的实现无须乘法器,节省了FPGA片内资源。实验证明按照级联结构进行设计时,128阶FIR滤波器需要占用3000个LE以上,提高时钟重复利用乘法器后为1500LE,而采用分布式的结构资源消耗仅为900多个LE。希尔伯特滤波器由于阶数较低,消耗的资源更少。假定数据h(n)为B位,FIR的阶数为N,则需要的地址空间为2N,当N较大时实现会有困难。通过将128阶的滤波器分割为8块16阶的方法,有效减少了存储容量。该结构既节省资源又灵活。利用线性相位FIR滤波器的对称性,还可以节省一半存储量。
3 载波发生器的实现
电力线路中影响衰减特性的因素很多,这就要求电力线载波机线路调制单元的载波频率可变。NCO可以产生不同频率的正弦信号抽样值。如图3所示,预先存储一张正弦信号ROM表,表中放有8192个抽样点的值。假设所需的载波频率为300kHz,NCO从ROM表中每隔300个点取出一个值,即可得到频率为300kHz正弦信号的抽样值。在实现中正弦信号ROM表的是通过对频率为1Hz的正弦信号在一个周期内进行8192次等间隔采样得到的。由于频率分辨率为1kHz,所以根据需要载波频率的不同,NCO改变抽取点间的间隔,就能在一定范围内得到任何1kHz整数倍频率的正弦信号抽样值。

图3 NCO内部原理图
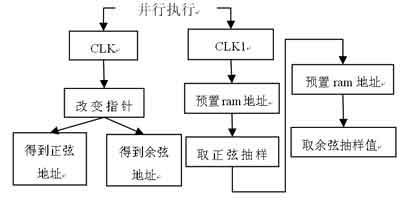
图4 NCO设计流程
正弦信号具有重复性,因此设计时只需存放四分之一个周期的值,即2048个抽样值。这样节约了大量的ROM空间和存储单元。NCO的流程如图4所示。
正弦信号和余弦信号仅仅是相位上偏差了90°,因此每次从ram中取正弦信号抽样值的时候,将地址指针延迟四分之一周期就能取出与之严格同步的余弦信号值。设计时NCO采用了双时钟结构,CLK为低频时钟,CLK1为高频时钟。在低频时钟内使用一个地址指针控制提取两路载波的地址,在高频时钟内根据地址依次提取正弦和余弦抽样值。低频时钟控制地址指针的变换,在时钟上升延到来时变更指针。CLK经过一个周期的时间内,CLK1经过6个周期:前三个周期空等待,等待地址指针m的刷新;而后的三个周期依次根据地址取出正弦余弦的抽样值,并作同步输出。

线路调制单元是电力线载波机中关键部件之一。为了提高频带的利用率,线路调制一般采用单边带调制方式。使用数字化处理方法来实现线路的单边带调制,能够克服模拟电路的诸多缺陷。线路调制需要完成正交变换、滤波和频谱搬移等处理,运算量与采样率直接相关。高采样率导致了高的运算量,低成本DSP芯片无法满足运算需求。FPGA可用于实现DSP运算处理单元,达到实时完成数字信号处理功能的目的,它为线路调制单元的数字化实现提供了一条性价比较高的途径。本文将介绍线路调制的FPGA实现,包括:线路调制单元数字化实现的总体设计,CIC和FIR滤波器的FPGA实现以及载波发生器单元的设计。
线路调制解调实现方案
电力线载波通信标准要求的信号频率为40~500kHz,频带宽度为4kHz。根据奈奎斯特定理,采样频率不能小于1MHz。采用数字化处理方式实现调制就是将信号的频谱搬移过程转化为数字域的数值计算过程。单边带信号可以表示为x(n)cos(wn)±x^(n)sin(wn),式中x(n)为基带信号,x^(n)为基带信号的正交信号,w为载波频率。由该式可知,完成单边带调制需要信号的正交变换、载波信号的产生、信号与载波的乘加等数值运算。希尔伯特变换是一种便于采用FPGA实现的正交变换方法,它可由系数具有奇对称特性的FIR滤波器实现。
基带信号的频率较低,相应应以较低的采样率采样,而调制信号的频率较高,应以较高的采样率采样。因此在调制过程中必须进行采样率的提升,内插技术可以实现采样率的变换。调制单元调制部分的数字化实现的逻辑结构如图1所示。

由图1可见,调制单元由正交变换、内插和调制三部分组成。完成正交变换的Hilbert滤波器为系数奇对称的FIR滤波器,延迟保持了正交信号与原始信号的时间同步。载波发生器,乘法器和加法器完成单边带调制。载波发生器由查表法实现,地址为13位,字长为16位,可以产生所需要的各种载波频率。内插完成采样率的提升,再用低通滤波器滤除无用频率分量。在设计中,通过内插将信号采样率由8kS/s提升至8.192MS/s,内插率I=1024。分两级完成:第一级内插率I=8,该级内插采用128阶系数偶对称FIR滤波器滤波。第二级内插率I=128,该级内插采用3级级联的CIC(积分梳状)滤波器。
由上述方案可见,合理设计FIR、CIC滤波器和载波发生器电路是线路调制单元数字化实现的关键,线路调制单元和其他的组件进行数据交换,控制和接口电路在此不作一一赘述。
滤波器的FPGA设计
线路调制解调需要用到FIR和CIC两种滤波器,这两种滤波器的共同特点是,具有线性相位,非常适合应用需求。但这两种滤波器对FPGA资源耗费较大,因此必须采用合理的结构减少FPGA资源的开销。
1 CIC滤波器的设计
设计CIC滤波器时,首先要考虑滤波器的增益,防止溢出。内插均选用三级级联的CIC滤波器,传递函数为H(z)=((1-z-128)/(1-z-1))3。由传递函数可以求出滤波器的增益为1283,增加的字长为log2(128)3=21位,输入信号宽度为13位,实现时必须预留21+13=34位防止溢出。将内插器与滤波器结合起来并对其实现如图2所示。

图2 cic内插
程序设计采用VHDL语言,用Quartus II 3.0综合后CIC滤波器耗费资源350个LE(Logic Element)。根据Hogenaur的剪除理论在每一级输出时都可以剪除掉最后的若干位。通过信噪比的计算,可确定剪除位数,设计中积分部分每级可以剪除6位,分别取22、28和34位,梳状部分每级剪除1位,分别取14、15和16位,滤波器的输出为13位。采用剪除理论后,消耗的资源为240个LE,资源消耗减少了32%。
2 FIR滤波器的设计
FIR滤波器阶数高,如果按其级联结构实现时资源的利用率非常低,须加以改进。一种方法是提高时钟速度,重复利用乘法器和加法器。这种方法程序设计比较复杂,时钟提升也导致功耗增加,额外资源的消耗较多。另一种方法是利用FIR滤波器的分布式结构进行设计,这是一种高效的方法。信号x(n)通过N抽头,n位的FIR滤波器可以用下式表示,其中h(n)是滤波器系数,y为输出信号。
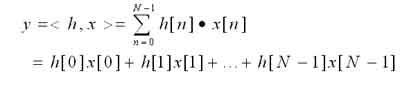
输入信号x(n)采用补码的形式,可表示为

重新对上式求和如下:
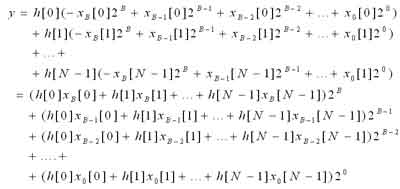
简写形式如下:
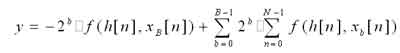
由上式可看出,把输入信号每位的值xb作为地址,将滤波器系数h(n)的值和xb的每一位xb(n)乘积叠加,并将结果存入ROM中,就可以通过查表并移位相加而得到最终内积的结果。整个滤波器的实现无须乘法器,节省了FPGA片内资源。实验证明按照级联结构进行设计时,128阶FIR滤波器需要占用3000个LE以上,提高时钟重复利用乘法器后为1500LE,而采用分布式的结构资源消耗仅为900多个LE。希尔伯特滤波器由于阶数较低,消耗的资源更少。假定数据h(n)为B位,FIR的阶数为N,则需要的地址空间为2N,当N较大时实现会有困难。通过将128阶的滤波器分割为8块16阶的方法,有效减少了存储容量。该结构既节省资源又灵活。利用线性相位FIR滤波器的对称性,还可以节省一半存储量。
3 载波发生器的实现
电力线路中影响衰减特性的因素很多,这就要求电力线载波机线路调制单元的载波频率可变。NCO可以产生不同频率的正弦信号抽样值。如图3所示,预先存储一张正弦信号ROM表,表中放有8192个抽样点的值。假设所需的载波频率为300kHz,NCO从ROM表中每隔300个点取出一个值,即可得到频率为300kHz正弦信号的抽样值。在实现中正弦信号ROM表的是通过对频率为1Hz的正弦信号在一个周期内进行8192次等间隔采样得到的。由于频率分辨率为1kHz,所以根据需要载波频率的不同,NCO改变抽取点间的间隔,就能在一定范围内得到任何1kHz整数倍频率的正弦信号抽样值。

图3 NCO内部原理图

图4 NCO设计流程
正弦信号具有重复性,因此设计时只需存放四分之一个周期的值,即2048个抽样值。这样节约了大量的ROM空间和存储单元。NCO的流程如图4所示。
正弦信号和余弦信号仅仅是相位上偏差了90°,因此每次从ram中取正弦信号抽样值的时候,将地址指针延迟四分之一周期就能取出与之严格同步的余弦信号值。设计时NCO采用了双时钟结构,CLK为低频时钟,CLK1为高频时钟。在低频时钟内使用一个地址指针控制提取两路载波的地址,在高频时钟内根据地址依次提取正弦和余弦抽样值。低频时钟控制地址指针的变换,在时钟上升延到来时变更指针。CLK经过一个周期的时间内,CLK1经过6个周期:前三个周期空等待,等待地址指针m的刷新;而后的三个周期依次根据地址取出正弦余弦的抽样值,并作同步输出。

PLC 模拟电路 DSP FPGA 滤波器 低通滤波器 电路 VHDL Quartus 相关文章:
- 基于ARM9和CPLD的输入输出系统设计(04-09)
- 在单个FPGA平台上采用多种工业以太网标准进行设计(03-13)
- CPLD器件在单片机控制器中的使用(07-24)
- 基于CPLD的电梯运行控制器的设计(10-10)
- PBGA向FBGA转变过程中的挑战(10-12)
- 基于梯形图VHDL的CPLD开发方法研究(11-07)
