车牌定位在电子警察中的工程应用

　近年来，我国在城市和交通建设方面取得了巨大的进步。然而，面对越来越多的交通路口、收费站以及治安卡口，传统的人工值守显然已经满足不了要求。为解决这种现状，出现了适应信息化时代的计算机集成产品，即电子警察，并已经得到了广泛的应用。

　　电子警察采用视频图像的识别技术，全天候进行车辆及道路的监控，对违规车辆进行抓拍，实现了城市道路交通的智能化管理，达到无人化值守。利用该系统可以迅速查明违章车辆、分析交通事故，为进一步整顿交通环境，交通管理科学化提供高效可靠的技术依据。

1 抓拍照片分析

　　出于性价比的原因，目前国内电子警察系统的图像获取单元一般都采用CCD工业电视摄像机，而且被架设在室外。现以闯红灯违章抓拍系统为例来分析抓拍的图像数据。

　　(1) 由于红灯的停车线靠近行人通道，造成图像背景特别复杂;

　　(2) 机动车的车型较多，车牌的位置各不相同;

　　(3) 拍摄图像时受天气、照明以及运动等因素的影响很大;

　　(4) 摄像机受路口实际条件的限制，可能距离较远，并有一定角度;

　　(5) 脏、旧车牌比较模糊，还有不少故意作弊的车牌。

　　这种图像数据要比在实验室所用的数据恶劣得多，而且意想不到的情况也时有发生，这就给图像识别带来了极大的困难。

2 图像处理方案

　　通过多次实验检测，最终选用了图1所示的图像处理方案。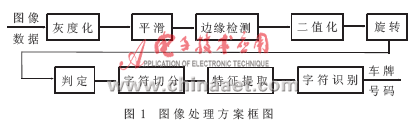

对图像数据的灰度化、平滑、边缘检测、二值化以及旋转都属于图像的预处理部分。判定就是准确地定位车牌位置，接下来先对车牌进行字符分割，然后逐字提取特征，形成该字符的特征向量，将这个特征向量作为神经网络的输入，以便于字符识别。所以字符识别部分用了一个三层的神经网络，先进行学习训练，得到收敛的一组权值。

限于篇幅，本文只介绍图像预处理和判定部分，识别应用部分这里就不讨论了。

2.1 灰度化与平滑

　　为了便于处理后的传输和存储，由CCD摄象机获取的图像通过图像采集卡采集到工控机或图像处理器件后，一般会转换成JPEG格式。这样处理的对象也就是JPEG文件，要进行灰度化，以去掉彩色信息，加快处理速度。灰度化的公式可以采用式(1)。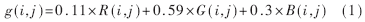

其中，g(i，j)为点(i，j)处的灰度值，R，G，B分别为该点的三基色值。但是，定位车牌时亮度信息并不重要。鉴于在这个式子中，G基色占的比重最大，所以有理由在灰度化时只取绿色信息就可以了。

　　图像平滑的目的是为了消除噪声。噪声并不限于人眼所能看到的失真或变形，有些噪声只有在进行图像处理时才能发现。一般来说，图像的能量主要集中在其低频部分，而车牌的信息主要在高频部分，为了去掉高频干扰，有必要进行图像平滑。可以采用低通滤波的方法来去除噪声，为此要设计空间域系统的单位冲激响应矩阵。


2.2 边缘检测与二值化

　　与平滑过程相反，边缘检测相当于高通滤波器，是为了提取图像中的高频部分。因为车牌上字符较密，所以这一部分的图像变化必然比其它区域高，这对于车牌定位是很重要的信息。边缘增强的方法很多，常用的增强算子有拉普拉斯算子、Sobel算子、Prewitt算子等。本文采用了一种Kirsch算子的改进形式。Kirsch算子是一种象素邻点顺时针循环平均求梯度的方法，它取如下的梯度图像作为检测结果: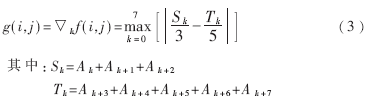

分别表示f(i，j)的八邻象素中顺时针排列的相邻三个象素和五个象素之和。规定A0为f(i，j)左上角的邻域。A的下标按模8计算，如图2所示。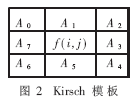

式(3)中大括号内的取极大值运算，其实就是求f(i，j)在8个方向上的平均差分之最大值，也就是f(i，j)梯度幅度的近似值[1]。

　　通过这种运算后，图像中每象素点的值代表了该点的高频信息，从这些信息中要定位出车牌的位置，就必须进行二值化处理。二值化的方法有很多，但应用于工程上时，一个最大的问题就是阈值的选取，将它取为固定值显然是不合理的，因为环境总是变化的;可是将它放开后，又不能很好地跟踪图像的细微变化。针对这个问题，本文提出了一种反向积分求象素点的方法，使得二值化能自适应选择适当的阈值。

其中:n(k)为图像中所有取值为k的象素点个数，n为图像总象素数。通过大量的实验，发现这个象素值-概率关系曲线无外乎两种情况，即图3和图4所示。要使定位效果达到最佳，阈值一定在曲线趋于平坦的点附近。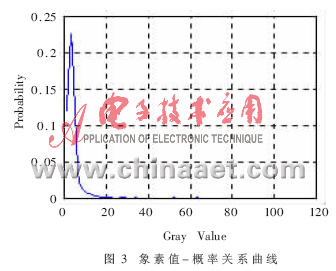

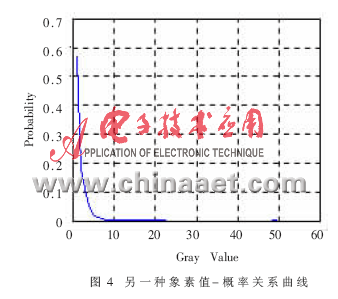
这时会发现不管是白天还是夜间，S总是在一常数附近，而这个差别对于象768×288这样的图像来说是微不足道的，完全可以将它定为一个常数来处理。虽然它也与图像的复杂程度有关，但这只会影响二值化后点的分布。车牌位置总是处于高频部分，对它的影响较小。这个现象也同时说明，要准确定位并不是二值化后保留的信息越多越好。

既然将S取为常数，那么