应用两级分类实现车牌字符识别

车牌识别系统LPR(License Plate Recognition)包括车牌定位、字符分割和字符识别三大部分。其中，字符识别的准确及高效成为整个车牌识别系统的关键。

车牌字符识别是模式识别的一个重要研究领域，字符特征提取可分为基于统计特征和基于结构特征两大类[1]，统计方法具有良好的鲁棒性和抗干扰性等，但是，由于其采用累加的方法，对于"敏感部位"的差异也随之消失，即对形近字的区分能力较差。而结构方法对细节特征较敏感，区分形近字符的能力较强，但是难以抽取、不稳定、算法复杂度高。分类器设计方面，人工神经网络和支持向量机SVM(Support Vector Machine)[2]等技术已被用于车牌字符识别研究中，有效地提高了识别率，但缺少基于特征的优化设计。

本文针对实际采集的车牌图像质量不高所导致的字符形变、噪声、易混淆的问题，根据人类视觉活动的问题，选取基于轮廓的统计特征反映字符整体信息；选取结构特征反映字符细节信息，采用SVM作为分类器，并对基于轮廓的特征提取方法进行了优化设计。

1 车牌字符识别算法框架

本文提出的识别算法模拟人类智能，采用两级分类识别的思想处理车牌字符识别问题，引入可信度评判机制。经预处理后的字符首先进入粗分类识别，采用基于轮廓的统计特征作为粗分类的特征提取方法，利用SVM分类器得出分类识别结果，并计算结果的可信度。识别系统将粗分类识别结果的可信度与预先设置好的用于判别形近字的可信度阈值相比较,如果可信度大于阈值,则识别系统将字符归为非形近字,并将结果输出;否则, 识别系统将字符归为形近字,并根据粗分类识别结果,计算字符所属的形近字类别,将字符送入细分类识别,提取字符的结构特征作为细分类的特征提取方法，利用决策表中的形近字区分规则，得到识别结果。图1为识别系统算法流程图。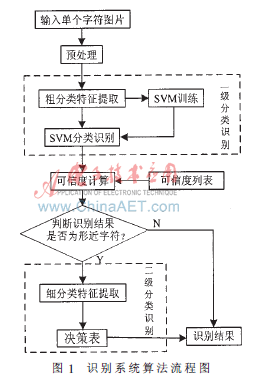


2 一级分类识别

2.1 粗分类特征提取

粗分类的特征提取方法应该能够描绘字符的整体信息，基于轮廓的统计特征描绘字符外围轮廓的变化。利用距离反映轮廓的方法，通过计算字符图像左、右、上、下四个边框到笔画间的距离，得到图像轮廓的统计特征。设预处理后的二值化字符图像为f(i,j)，具体算法为：

其中,width、length为字符图像的宽和高。规定此行或此列没有笔画时，其特征值为零。

图2为字符‘6’的四组轮廓特征，从图中可以看出，曲线在高度变化上反映出了字符外围轮廓特征。根据轮廓特征曲线可以找出同类字符间的相关性、不同类字符间的差异性。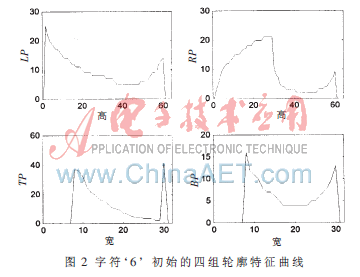

然而，这样直接提取的特征容易受到字符偏移的影响，因此，本文对提取的原始特征进行了如下优化：
(1)分别循环平移特征值LP(i)、RP(i)、TP(i)、BP(i)，使其前后为零特征值的个数大致相等，这样提取的特征值在分类器中更具可比性。

(2)由于字符存在水平偏移和垂直偏移，所以需要消除字符偏移对特征值的影响。首先，按照下式计算字符水平偏移量LO：

其中，[·]表示取整数。
消除垂直偏移量对特征值的影响与消除水平偏移量方法类似，这里不再重复。

图3所示为图2优化后的特征曲线。从图中可以看出，优化后的特征曲线左右为零值的特征数量大致相等，第一、二组的最小特征值大致相等，第三、四组最小特征值也大致相等。由此可见，依据上述优化方法对四组轮廓特征加以修正，可以有效地克服字符位置偏移对特征值的影响，增加同类字符间的相关性。


2.2 一级粗分类器设计

本文提取的粗分类特征维数比较大,SVM能够较好地解决小样本、非线性及高维的模式识别问题，而且在高维空间中的推广能力并不受维数影响,所以本文选取SVM作为分类器进行车牌字符的识别。

2.2.1 支持向量机(SVM)算法原理

SVM是建立在统计学习理论的VC维(Vapnik-Chervonenkis Dimension)理论和结构风险最小化原理SRM(Structural Risk Minimization)基础上的一种新机器学习系统[3]。SVM方法是从线性可分情况下的最优分类面提出的。对于线性不可分情况，SVM通过增加一个松弛项ξi≥0和对错分样本的惩罚因子C进行推广。而对于非线性问题，首先通过非线性变换将输入空间变换到一个高维内积空间，然后在这个新空间中求取最优超平面。由于在特征空间H中构造最优超平面时,训练算法只涉及训练样本之间的内积运算(xi·xj)。

2.2.2 核函数的选取

根据Hilbert-Schmidt原理,只要一种核函数K(x,y)满足Mercer条件，它就对应某一变换空间中的内积。K(x,y)只涉及x、y，并没有高维运算。由此可见，核函数的引入避免了非线性映射计算的复杂性。有研究表明，SVM方法并不十分依赖核函数的选取，即不同的核函数对分类性能影响不大，所以本文选取应用广泛的径向基核函数(RBF)作为核函数：


2.3 可信度

可信度是不确定性推理中用于度量证据、规则和结论不确定性的一种方法。由于多种因素的影响，车牌字符识别过程中存在一定的不确定性，所以本文引入不确定性推理来判断识别结果是否可以被信任。

2.3.1 可信度概念

可信度CF用于度量证据、结论和规则的不确定性程度[6]，CF的作用域为[-1,1]。设一个不确定推理过程的证据为A,结论为B,推理规则为：IF A THEN B。
(1)证据的不确定性度量：CF(A)表示证据的可信度，CF(A)＞0，表示A以CF(A)程度为真；CF(A)＜0，表示A以CF(A)程度为假。
(2)规则的不确定性度量：CF(B,A)表示规则的可信度。CF(B,A)＞0，表示证据增加了结论为真的程度；反之CF(B,A)＜0，表示证据增加了结论为假的程度。

当CF(B)的值大于形近字判别阈值CFmin时，直接输出粗分类识别结果;反之，分类器查找形近字所属类别，并将字符送入二级分类识别。

2.4 粗分类实验和分析

粗分类中字母和数字共有33类，每类有100个样本。其中每类用60个样本进行SVM训练，构造SVM分类器，剩下的40个样本做测试。

本文对粗分类器在不同可信度阈值下的性能进行了测试，测试结果如图4所示。从图中可以看出，粗分类识别率随着可信度阈值的增加而提高，但阈值设置太高时，粗分类有较高的拒识率，而将字符送入二级分类识别，导致浪费粗分类器的识别能力。所以可信度阈值选取0.7，粗分类器的识别性能最佳。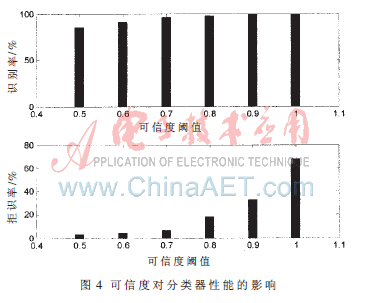

当CFmin=0.7时,粗分类字符识别正确率只有96.4%，但是出现错误的字符基本上都是形近字。如8、B、O、D、Q，2、Z，5、S等外形比较相似的字符，这些形近字符的差别体现在细微的结构上。如果将这些形近字符暂时归为一类，然后将其送入二级分类识别，则粗分类识别正确率会大幅提升接近100%,这样的结果可以满足特征提取算法复杂度低，识别率较高、形近字较少的粗分类的要求。