基于SVM不对称六相永磁电机控制系统的设计方案

永磁同步电动机(PMSM)因其高功率密度、高转矩和免维修等原因，广泛应用于高效驱动领域。六相永磁同步电动机发展了三相永磁同步电动机的结构，多应用于船舶电动推进等领域，它相对于普通永磁同步电动机而言有诸多优势，如船舶推进系统中，电流谐波最低次数要比一般三相电机高，降低了谐波幅值，提高了系统稳定性，减小转矩脉动，提高了电机工作效率，同时减小了转子谐波损耗，另外一旦发生缺相等故障，系统仍然可以继续运行。

随着电力电子技术的发展，电机变频调速系统在各种领域迅速发展和应用。直接转矩控制策略是在矢量控制策略之后最新兴起的变频调速技术，具有结构简单，动态响应快，鲁棒性强等优点。该技术最早是二十世纪80年代由德国教授Depenbrock和日本学者Takahashi分别提出的。主要应用于感应电机控制系统。于90年代末由L Zhong、M.F.Rahman和Y.W.Hu等人将其应用到永磁同步电机控制中。

本方案中所介绍的这种六相永磁同步电机具有六相不对称的结构，是一种船舶推进用电机。在Simulink中没有对应的模型。文章对六相电机模型进行分析同时进行了建立数学模型，并用Simulink对电机进行建模并封装。本文使用Simulink对不对称六相永磁同步电机直接转矩控制系统设计和仿真。同时对直接转矩控制系统进行建模，完成整个系统的搭建，同时加入空间电压矢量控制提高系统稳态转矩和电流，降低转矩脉动，并且对仿真结果进行了简单分析。

2.不对称六相永磁同步电机的数学模型

六相PMSM数学模型与$三相电动机很相似，为使分析方便，假设：①不考虑铁心饱和效应;②涡流和磁滞损耗忽略不计;③转子不设阻尼绕组;④认为每相绕组完全对称，定子电流、转子磁场对称分布;⑤近似认为反电动势波形为正弦。

坐标变换。

在PMSM瞬态运行过程中，对电机运行状态方程的求解和电机动态分析相当困难，主要原因是电机转子在磁、电结构上不对称，以及电机的电磁参数(电压、电流、磁链、转矩)的微分形式具有多种表达方式。因而在此采用坐标变换，通过消除时变参数，将变系数转化为常系数来求解，进而简化运算和分析过程。

本文采用两相旋转坐标系(dd-qq坐标系)来对PMSM电机的稳态性能进行分析，同时也可以对其瞬态性能进行分析。本文所采用的坐标系与定子磁场保持同步状态，dd轴滞后qq轴90°，dd轴的取向与转子总磁链的方向一致，成为转子磁场坐标系，A、B、C、D、E、F坐标系统与dd-qq坐标系的关系如下为六相静止坐标系到两相旋转坐标系的变换矩阵可以表示为式(1)：

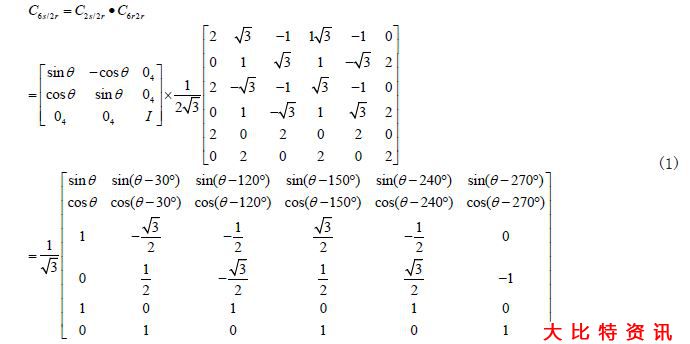
经过坐标变换可得，d-q坐标系下六相PMSM定子侧的电压方程、同时六相永磁同步电动机的磁链方程和转矩方程如式(2)-式(6)。

其中：Ud、Uq为d、q定子的电压分量;id、iq为d、q轴定子的电流分量; d ψ 、q ψ 、为d、q轴定子磁链分量;Ld、Lq为d、q轴电感分量;R为定子电阻;np为极对数; sω 为同步角速度;f ψ 为永磁体磁链;p为微分算子d/dt.

通过6/2变换，极大的简化了两相旋转坐标系下的六相PMSM的数学模型，降低了微分方程阶数，d轴磁链d ψ 和q轴磁链q ψ 不再是角度θ 的函数，这为$六相永磁同步电机的高性能转矩控制打下了坚实的基础。

在仿真过程中由于Simulink中没有现成的六相永磁同步电机模型，于是根据数学模型式(1)~(6)建立了六相永磁同步电机电机模型并对其进行了封装封装。

3.不对称六相永磁同步电机的直接转矩控制系统构成

对于永磁同步电机的直接转矩控制，其主要思想是在保证定子磁链幅值恒定的前提下，根据电机的负载角δ 和电磁转矩的正比关系，通过控制定子磁链的旋转方向来控制负载角δ进而控制电机的电磁转矩。δ 是定子磁链与转子磁链矢量相对于A轴的空间电角度的空间相位差。不对称六相永磁同步电机直接转矩控制系统组成结构如图1所示，系统包括：$电动机模块、逆变器模块、坐标变换模块、定子磁链观测模型、转矩估测模型、磁链和转矩的滞环比较器模块，定子磁链分区表、以及电压空间矢量表。