二维9／7小波变换VLSI设计

要输入的原始数据矩阵。Mesh结构中每一行最左边的PE都有一个数据输入信号线，原始数据矩阵的每一行的数值输入到PE阵列最左边的PE，然后依次输入对应PE。Mesh结构的第1列的PE有4个原始数据，最后一列PE有3个原始数据，其他PE都有2个原始数据，这样原始数据矩阵D的39x39个数值就对应于Mesh结构的39x18个PE的阵列中。矩阵D的元素在Mesh结构PE中的分配情况如图5所示。

(2)行变换 输入原始数据后，Mesh结构中的每一行的PE相互配合，完成“行变换”。从数值上，行变换结果为一个高频矩阵H和一个低频矩阵L。从Mesh结构上看，1个PE存储2个数值h和l，分别为矩阵H和矩阵L中的元素。但并不是每个PE中都存有h和l，因为Mesh结构的第1列和第18列的PE功能是边缘处理。所以行变换后，第2―17列PE有2个中间结果h和l。行变换结果高频矩阵H和低频矩阵L在Mesh结构中的存储情况，如图6所示。

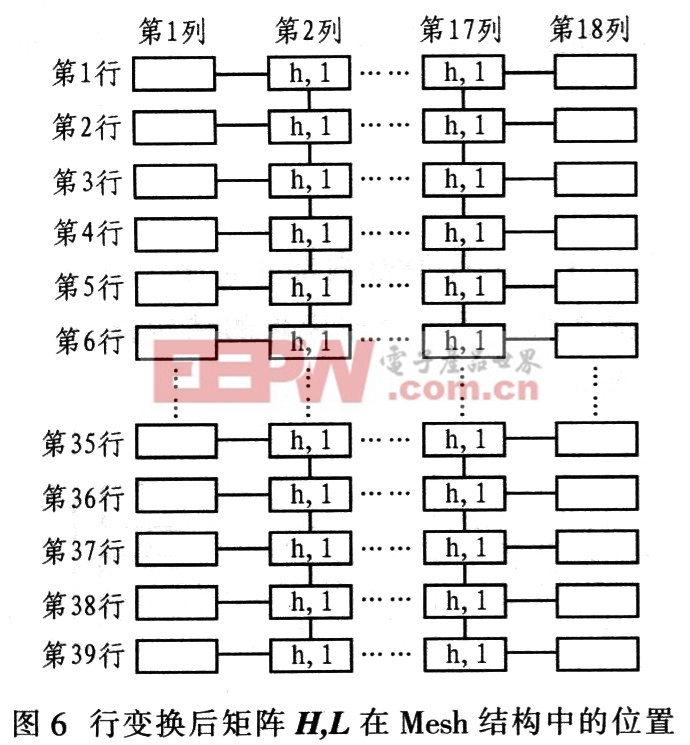
(3)数据交换 在进入列变换之前，需要调整h和l在PE中的位置，该过程就是数据交换。以图6中的第2列说明数据交换，其他列的数据交换和第2列的数据交换方法相同，如图7所示。

(4)列变换 数据交换后，PE在列上配合完成“列变换”。仍以第2列为例，从图7中看出，数据交换后，有的PE存储2个h，有的PE存储2个l。列变换就是含有2个h的PE之间的相互配合，2个l的PE的相互配合。从数值上看，列变换把H矩阵分为HH和HL矩阵，把L矩阵分为LH和LL2个矩阵。这4个矩阵的元素在PF中对应的位置如图8所示。

4 图像的边缘处理
真实信号具有边界，在某些一维应用中，信源产生的样本数量是无限的，能够忽略边界效应。二维的信源如图像，由于物理约束而有界，必须考虑小波变换的边界效应。边界延拓算法主要有零填充法、边界元素复制法、周期延拓法，对称延拓法和双倍对称延拓法。该设计采用对称周期延拓算法，就是预先拓展边界的数据点，将原信号X[k]延拓后的信号X’[k]送入提升结构中。例如：原信号集合为{X[0]，X[1]，X[2]，X[3]，X[4]…X[n一3]，X[n一2]，X[n-1]}，对于9／7奇对称小波，延拓后提输入信号为{X[4]，X[3]，X[2]，X[1]，X[0]，X[1]，X[2]，X[3]，X[4]…X[n一3]，X[n一2]，X[n―l]，X[n一2]，X[n一3]，X[n一4]}。要处理的图像是512x512像素，Mesh结构阵列中处理的是该图像的一个子图像。这样把图像分解为了16x16个子图像(32x32像素)。其处理顺序是：先对第1行的子图像从左到右处理，然后对第2行的子图像从左到右处理，依此类推，直到完整个512x512像素的图像处理为至。
一个子图像在调入处理阵列之前需经边缘处理。根据子图像所处位置不同，其图像处理也不同。比如对子图像G(1，1)，每行左边缘需要对称处理，而右边缘则取G(1，2)每行左边的3个像素点数值，每列上边缘做对称处理，每列下边缘取G(2，1)的每列上边3个像素点。这样经边缘处理后的子图像的像素为39x39。

5 比较
图像二维离散小波变换硬件实现有图9和图10所示的2种方法，图9是利用一维小波变换器直接实现图像的二维小波变换。图10是用行滤波器和列滤波器实现图像的二维小波变换。

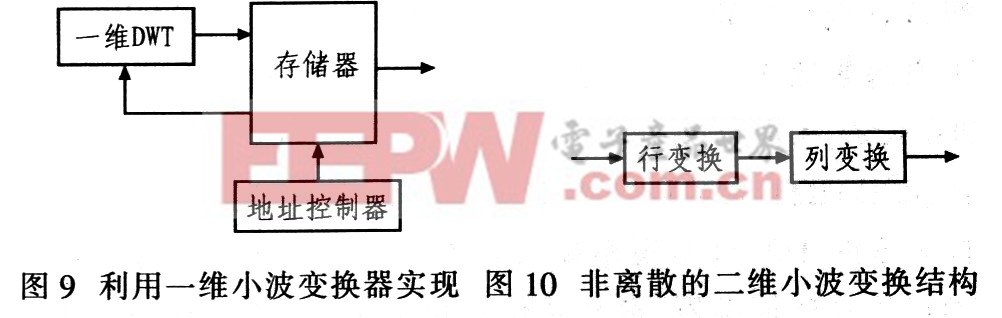
离散结构在行变换和列变换中间需要一个专用存储器来存储中间结果，Mesh结构在行变换后可直接列变换，这样可节约存储资源。而非离散结构采用行变换和列变换2个滤波器，Mesh结构用一个滤波器PE完成行变换和列变换，这样可节约计算资源。

6 结论
集成电路的频率取决于信号传输路径上两个寄存器之间的最大规模的组合逻辑。Mesh结构的设计中两个寄存器之间最大规模的组合逻辑为两个多路选择器和一个乘法器。参考文献中处理时最大的组合逻辑为一个乘法器。所以Mesh结构的设计和参考文献中的设计的频率基本相同，周期也相同。该系统设计处理32x32像素点需要31个周期，而其他设计中要逐个处理32x32个像素点，所以处理1 024(32x32)像素点需要l 024个周期。由于采用并行处理，这种Mesh结构的速度可提高32倍。