基于谐波频谱的LCL滤波器设计

摘要：此处研究了基于谐波频谱的LCL滤波器设计。针对LCL滤波三相并网逆变器，给出采用空间矢量脉宽调制(SVPWM)方法控制的逆变桥桥臂电压输出谐波。依据EMI滤波器设计的方法，研究谐波频谱与谐振频率之间的关系，得出LCL滤波器的谐振频率。在此基础上，设计出满足并网要求且总电感量最小的LCL滤波器。最后通过三相并网逆变器的实验装置给出了LCL滤波器设计方案的实验效果。

关键词：滤波器；谐波频谱；谐振频率

1 引言

地球上的石油及煤的储量有限，且化石能源的燃烧所排放的废气是造成环境污染、全球气候恶化的重要因素。核能发电的安全性及对环境的长期影响，目前还存在争议。世界各国都在努力寻求新的、“清洁”的发电方式，如风能、太阳能电能。在大功率风力并网逆变系统中，逆变器是实现电能馈送的一个重要环节。但是当功率较大时，为了减小损耗，功率器件的开关频率较低，导致进网电流具有较大谐波。为了使逆变器满足并网要求，且滤波器体积较小，通常采用LCL滤波器。

虽然LCL滤波器滤除高次谐波效果明显，但其设计比较复杂。文献介绍了LCL滤波器参数的设计步骤及限制条件，但过程较复杂，需要一定的实际经验，且需要多次尝试、反复验算才能得到合适的参数。文献给出了不同调制方法下，逆变器桥臂输出电压的谐波频谱。在此参考EMI滤波器的设计方法，在谐波频谱的基础上，得到谐振频率。然后根据系统功率确定LCL电容容值，在此基础上，计算出网侧电感值以及逆变桥侧电感值取值范围，根据取总电感量最小的原则，选择网侧电感以及逆变桥侧电感的感值。仿真和实验验证了滤波器设计方法的正确性。

2 LCL滤波三相并网逆变器的数学模型

三相并网逆变器的拓扑结构如图1所示。

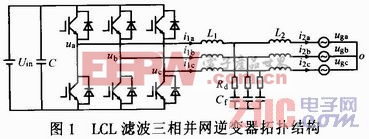
图中L1为逆变器侧电感，L2为网侧电感，Cf为滤波电容，Rd是为避免LCL滤波器出现零阻抗谐振点而设置的阻尼电阻，ua，ub，uc分别为三相逆变桥输出电压，uga，ugb，ugc分别为三相电网的相电压，i2a，i2b，i2c为网侧相电流；C为直流母线电容。

假设三相电网电压对称，主电路开关器件为理想开关元件，忽略阻尼电阻对电路的影响，那么根据基尔霍夫定律可得逆变器的基于开关函数的数学模型为：

由上述公式可知，进网电流与逆变桥输出电压的传递函数为：

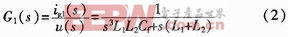
3 SVPWM控制的桥臂电压谐波分析

假设解析过程存在两个时间变量：x(t)=ωct+θc和y(t)=ω0t+θ0，其中载波角频率ωc=2π／Tc，Tc为载波周期，θc为载波波形的任意相位偏移角，基波(正弦)角频率ω0=2π／T0，ω0ωc，T0为基波周期，θ0为基波的任意相位偏移角。

双变量控制波形傅里叶谐波分量的表达式为：

式中：m为载波的索引变量；n为基带的索引变量。

然后可得到双边沿自然采样SVPWM下三相逆变器相桥臂的谐波解析式为：

对1≤k≤10范围内的项求和，就可得到精确度可以接受的谐波幅值。

4 滤波器设计方法

这里采用插入电压增益来设计滤波器。插入电压增益定义为滤波器插入前后负载端的电压比。根据定义的插入增益，滤波器的设计可遵循以下步骤：①通过仿真或者测试得到未加入滤波器时变换器产生的干扰噪声频谱；②计算需要的衰减值曲线Ureq：将未加入滤波器时测得的干扰值U与标准Ulim进行比较，再加上6 dB的安全裕量，即Ureq=U-Ulim+6 dB；③计算滤波器的转折频率：用滤波器的电压插入增益去交截②中得到的需要衰减的曲线值，交截得到的频率即为滤波器的转折频率，如图2所示；④设计滤波器参数并测试这些参数是否满足标准要求。

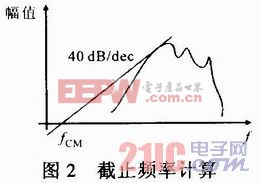
5 谐振频率计算

考虑类似于EMI滤波器的设计方法。首先根据进网电流标准，得到标准限值频谱，然后根据不同的PWM控制方法，得到桥臂输出电压的频谱及所需要的衰减，计算出谐振频率。由数学模型可知进网电流与逆变桥侧输出电压的传递函数，类似于插入电压增益的计算，可得到LCL滤波器中的电压增益为：

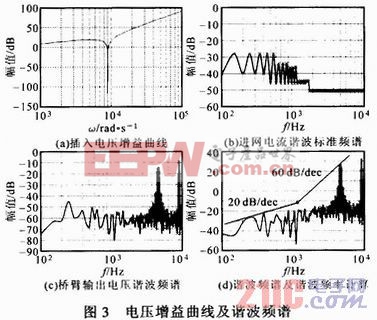
在对数域中：桥臂输出电压谐波-进网电流谐波+20log(I额定／U额定)=20log[s3L1L2Cf+s(L1+L2)]，LCL滤波器插入电压增益曲线如图3a所示。根据标准IEEE Std 929-2000，可绘出如图3b所示的进网电流谐波标准频谱曲线。当开关频率为5 kHz时，采用SVPWM的逆变器桥臂输出电压谐波频谱如图3c所示，图3d为系统中逆变桥输出电压各次谐波值减去进网电流各次谐波值。由于使用LCL滤波器，因此用20 dB／dec及60 dB／dec的直线去交截即可得出谐振频率。由图可知，此系统的谐振频率为1 300 Hz。

6 LCL滤波器中其他参数设计

由上述方法得到LCL滤波器的谐振频率，其计算公式如下：

因此在已知谐