一种基于d-q变换的谐波电流检测方法
时间:04-26
来源:电子元器件应用
点击:
0 引言
目前,谐波抑制的一个重要趋势是采用有源电力滤波器(Active Power Filter-APF)。而该滤波器性能的好坏与它所采用的谐波电流检测方法有很大关系。因此,如何实时准确地检测出非线性负载电流中的谐波及无功电流是有源电力滤波器(APF)的关键技术。瞬时功率理论是最适合有源电力滤波器对谐波进行实时检测的方法,目前基本上采用低通滤波器滤波(LPF)方式得出基波电流分量,然后与被检测电流相减,最终得出谐波电流分量。本文则给出另一种方法,即直接使用高通滤波器(HPF)来得到谐波电流分量,而不再需要与被检测电流相减,从而使检测装置得到进一步简化。
1 基本原理
以三相电路|0">三相电路瞬时无功功率理论为基础,采用同步旋转park变换的d-q的基本思想是将a-b-c坐标系下的电流量变换到d-q两相正交坐标系下来研究。设三相电压、电流是平衡且无零轴分量,那么,将三相负载电流iLa、iLb、iLc变换到d-q坐标系下,可得:
其中:
采用MATLA的SIMULINK软件进行仿真时,其检测电路模型可按照图1的原理进行搭建,模型的参数选择为:电源为工频220 V,电源支路上的,Rs=0.3Ω,Ls=0.3 mH;谐波源为三相整流桥电路的交流侧电流,直流侧接的电阻电感负载R1=8Ω,L1=80 mH。这种情况下,整流桥的交流侧电流可近似为方波。其仿真波形如图2所示。
其中,图2(a)为a相电网电压ea和被检测电流ila波形图,b、c两相的电压和电流波形相同,但相位分别滞后120°和240°。图2(b)和图2(c)分别为采用高通和低通滤波器所得到的谐波分量波形,而图3则分别给出了采用低通滤波器所得到的谐波分量频谱图,由图可见,其高通和低通两波形基本一致,同时两频谱图也基本一致,这说明该方法能准确检测出谐波分量。
目前,谐波抑制的一个重要趋势是采用有源电力滤波器(Active Power Filter-APF)。而该滤波器性能的好坏与它所采用的谐波电流检测方法有很大关系。因此,如何实时准确地检测出非线性负载电流中的谐波及无功电流是有源电力滤波器(APF)的关键技术。瞬时功率理论是最适合有源电力滤波器对谐波进行实时检测的方法,目前基本上采用低通滤波器滤波(LPF)方式得出基波电流分量,然后与被检测电流相减,最终得出谐波电流分量。本文则给出另一种方法,即直接使用高通滤波器(HPF)来得到谐波电流分量,而不再需要与被检测电流相减,从而使检测装置得到进一步简化。
1 基本原理
以三相电路|0">三相电路瞬时无功功率理论为基础,采用同步旋转park变换的d-q的基本思想是将a-b-c坐标系下的电流量变换到d-q两相正交坐标系下来研究。设三相电压、电流是平衡且无零轴分量,那么,将三相负载电流iLa、iLb、iLc变换到d-q坐标系下,可得:

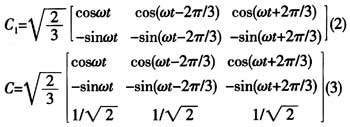
其中:
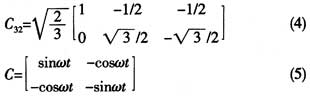


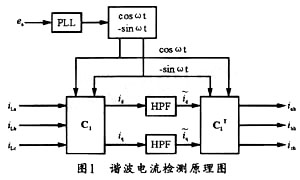
采用MATLA的SIMULINK软件进行仿真时,其检测电路模型可按照图1的原理进行搭建,模型的参数选择为:电源为工频220 V,电源支路上的,Rs=0.3Ω,Ls=0.3 mH;谐波源为三相整流桥电路的交流侧电流,直流侧接的电阻电感负载R1=8Ω,L1=80 mH。这种情况下,整流桥的交流侧电流可近似为方波。其仿真波形如图2所示。
其中,图2(a)为a相电网电压ea和被检测电流ila波形图,b、c两相的电压和电流波形相同,但相位分别滞后120°和240°。图2(b)和图2(c)分别为采用高通和低通滤波器所得到的谐波分量波形,而图3则分别给出了采用低通滤波器所得到的谐波分量频谱图,由图可见,其高通和低通两波形基本一致,同时两频谱图也基本一致,这说明该方法能准确检测出谐波分量。
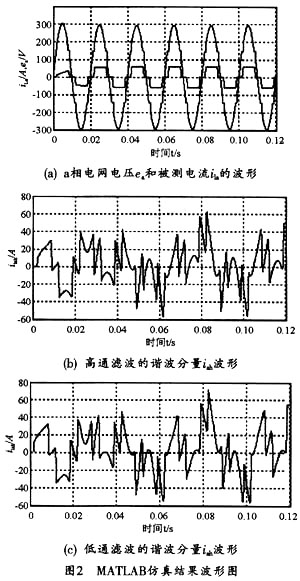
3 结束语
本文对该谐波检测方法进行了理论分析。该方法根据瞬时无功功率理论,将三相整流电路交流侧电流经过坐标变换得到id、iq,然后利用高通滤波器(HPF)分离出其中的交流分量,再经过坐标反变换获得谐波电流分量,最后进行MATLAB仿真实验。实验结果表明,与低通滤波方法相比,该方法不仅能快速准确地检测出谐波分量,而且能使谐波检测得到进一步简化。
- 基于瞬时无功功率理论的改进型有源电力滤波器的数字化研究(05-02)
- 电能质量控制装置的指令信号检测方法(03-18)
- 基于新型方波有源电力滤波器检测指定谐波次数电流的方法(04-29)
- 零线谐波电流阻断器特点及应用(07-30)
- 三相电路教学与实验相结合的改进(10-26)
- 无需调谐的“砖墙式”低通音频滤波器(11-20)
