高频链逆变器的重复控制策略研究
时间:05-26
来源:国外电子元器件
点击:
l 引言
双向电压源高频链逆变器|0">逆变器因其变换效率高、功率密度大、易于用在大功率场合,目前是光伏逆变电源领域的研究热点。在电压源型高频链逆变电源模型的基础上建立了逆变器连续时间域和离散时间域的数学模型。研究了基于电压反馈的离散重复控制技术,分析了重复控制消除输出电压周期性波形畸变的原理。最后,应用PSIM仿真软件进行了系统试验,对关键的试验波形做出了分析。
2 逆变器主电路数学模型的建立
双向电压源高频链逆变器原理图如图1所示.它是以Forward为基本单元。直流输入电压DC通过高频逆变器逆变,在变压器原边得到高频正负脉冲,通过高频变压器进行变压比调整和电气隔离,变压器副边得到和原边相位相同的高频正负脉冲波,周波变换器对高频脉冲进行低频解调,在输出滤波电路两端得到低频交流脉冲电压,再由滤波电路滤除高次谐波。
利用MATLAB可求得系统传递函数的离散形式为:
3 重复控制策略
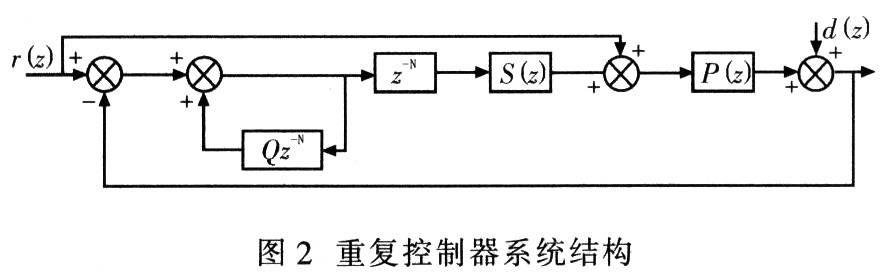
重复控制是一种基于内模原理的控制策略,其作用是当输入信号以基波周期重复出现,输出对输人信号的逐周期累加,即使输入衰减至零,内模仍然会持续不断地逐周期重复输出与上周期波形相同的信号。将这个周期信号保持器引入到反馈控制系统内部,并通过补偿环节使系统稳定,可在一个周期内跟踪给定并且消除扰动。重复控制系统结构如图2所示,它包括重复控制器内模、周期延时环节及补偿器S(z)。
每基波周期对输出电压的采样次数,N=fc/f。其中fc为参考输入基波频率,f为载波频率。
3.2 补偿器的设计
由被控系统P(z)幅频特性曲线可知:在ω=4 564 rad/s处有一谐振尖峰。补偿器S(z)用以消除该谐振峰。选取二阶振荡环节在中低频段与P(z)对消,在高频段急剧衰减,其中ζ=l,ωn=4 600。为了改善补偿性能,设计中引入Notch函数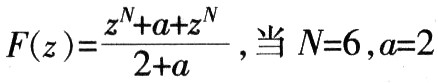 时对谐振尖峰起陷波作用。则完整的补偿器形式为:S(z)=S1(z)F(z)。
时对谐振尖峰起陷波作用。则完整的补偿器形式为:S(z)=S1(z)F(z)。
3.3 zKKrQ(z)的设计
被控对象P(z)和补偿器S(z)都存在着很大的相位滞后,所以采用相位补偿环节Zk进行补偿。通过相频曲线比较确定,当k=10时,S(z)P(z)与z-10与在中低频段吻合,相位得到补偿。Kr的取值范围是O~1,类似一个比例控制器的功能。本例中,Kr取0.21可得到满意的调节效果。
Q(z)应为接近1的常数,当Q(z)取小于1的常数时,使得原点为Q(z)端点的单位圆整体左移,可以保证系统在全频段的稳定性,本例中取经验值0.95。
3.4 仿真实验
在阻性和阻感性负载条件下,对系统进行仿真,比较输出电压与参考输入的波形结果如图3、图4所示。
双向电压源高频链逆变器|0">逆变器因其变换效率高、功率密度大、易于用在大功率场合,目前是光伏逆变电源领域的研究热点。在电压源型高频链逆变电源模型的基础上建立了逆变器连续时间域和离散时间域的数学模型。研究了基于电压反馈的离散重复控制技术,分析了重复控制消除输出电压周期性波形畸变的原理。最后,应用PSIM仿真软件进行了系统试验,对关键的试验波形做出了分析。
2 逆变器主电路数学模型的建立
双向电压源高频链逆变器原理图如图1所示.它是以Forward为基本单元。直流输入电压DC通过高频逆变器逆变,在变压器原边得到高频正负脉冲,通过高频变压器进行变压比调整和电气隔离,变压器副边得到和原边相位相同的高频正负脉冲波,周波变换器对高频脉冲进行低频解调,在输出滤波电路两端得到低频交流脉冲电压,再由滤波电路滤除高次谐波。


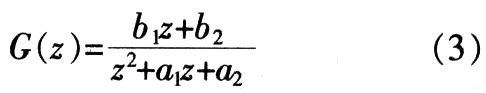
利用MATLAB可求得系统传递函数的离散形式为:
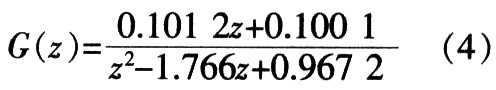
3 重复控制策略
重复控制是一种基于内模原理的控制策略,其作用是当输入信号以基波周期重复出现,输出对输人信号的逐周期累加,即使输入衰减至零,内模仍然会持续不断地逐周期重复输出与上周期波形相同的信号。将这个周期信号保持器引入到反馈控制系统内部,并通过补偿环节使系统稳定,可在一个周期内跟踪给定并且消除扰动。重复控制系统结构如图2所示,它包括重复控制器内模、周期延时环节及补偿器S(z)。
每基波周期对输出电压的采样次数,N=fc/f。其中fc为参考输入基波频率,f为载波频率。
3.2 补偿器的设计
由被控系统P(z)幅频特性曲线可知:在ω=4 564 rad/s处有一谐振尖峰。补偿器S(z)用以消除该谐振峰。选取二阶振荡环节在中低频段与P(z)对消,在高频段急剧衰减,其中ζ=l,ωn=4 600。为了改善补偿性能,设计中引入Notch函数
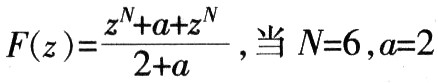 时对谐振尖峰起陷波作用。则完整的补偿器形式为:S(z)=S1(z)F(z)。
时对谐振尖峰起陷波作用。则完整的补偿器形式为:S(z)=S1(z)F(z)。 3.3 zKKrQ(z)的设计
被控对象P(z)和补偿器S(z)都存在着很大的相位滞后,所以采用相位补偿环节Zk进行补偿。通过相频曲线比较确定,当k=10时,S(z)P(z)与z-10与在中低频段吻合,相位得到补偿。Kr的取值范围是O~1,类似一个比例控制器的功能。本例中,Kr取0.21可得到满意的调节效果。
Q(z)应为接近1的常数,当Q(z)取小于1的常数时,使得原点为Q(z)端点的单位圆整体左移,可以保证系统在全频段的稳定性,本例中取经验值0.95。
3.4 仿真实验
在阻性和阻感性负载条件下,对系统进行仿真,比较输出电压与参考输入的波形结果如图3、图4所示。

由图3可以看出,引入重复控制器后,系统在阻性负载条件下,谐波含量少,输出电压波形正弦度好;相位上也与基准电压保持一致。波形质量较好。由图4看出.重复控制对于波形幅值的调节效果不如阻性负载时.波形正弦度明显变差,谐波含量大。这说明重复控制对于随机干扰的抑制有一定困难,具有动态性能差的缺陷。但从结果也看出,引入重复控制后,相位调节效果好,输出波形相位与输入基准基本保持一致,这一点给逆变器波形控制以及逆变器的并联提供了一个有利条件。
4 结语
分析了逆变器领域常用的双向电压源高频链逆变器的结构和原理,研究了基于电压反馈的离散重复控制技术。通过实验可以看出,引入重复控制器后,系统输出波形的谐波含量明显减少,输出电压波形质量大大提高;在相位的调节上效果更加明显,使输出波形能够在相位上与输入基准保持一致,为逆变器的并联提供了有利条
- 反激式高频变压器的分析与设计(04-24)
- 双向电压源高频链逆变器(07-23)
- 电流源高频链逆变器(07-23)
- 三相电压源型高频链逆变技术(07-23)
- 三相电压源型高频链逆变器电路(07-23)
- 基于重复控制的全数字UPS逆变器(02-28)
