一种基于FPGA的彩色图像增强系统的设计
时间:11-09
来源:互联网
点击:
在从图像源到终端显示的过程中,电路噪声、传输损耗等会造成图像质量下降,为了改善显示器的视觉效果,常常需要进行图像增强处理。图像增强处理有很强的针对性,没有统一的评价标准,从一般的图片、视频欣赏角度来说,滤除噪声、扩展对比度、锐化以及色彩增强等处理能显著提升视觉效果。
这里设计一个基于FPGA的实时视频图像处理系统,包含增强对比度扩展和色饱和度两种处理方法,相比于DSP和ASIC方案来说,FPGA在性能和灵活性方面具有绝对优势,应用FPGA设计视频通信系统更普遍。
1 原理和算法
图像增强处理可以在频域和空间域进行,典型的频域方法如直方图增强处理,适合于软件系统实现;而硬件系统更适合于空间域处理,因此本文所述的处理方法都将在空间域进行。
1. 1 对比度扩展
对比度扩展又称灰度变换,其目的是在拓展感兴趣的灰度区间的同时,压缩不感兴趣的灰度区间。最简单有效的方法是线性变换,满足以下关系:
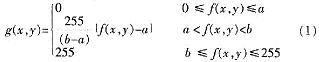
f(x,y)和g(x,y)分别表示输入图像和输出图像的灰度值。经过变换,线性拉伸了在a~b内的灰度值,同时对[0,a]和[b,255]灰度区间进行抑制。从显示设备的角度来说,一般民用级别的显示器都不具备完美表现256灰阶的能力,因此抑制过暗[0,a]和过亮[b,255]的灰度区间而增强中间区域的动态范围,可以避免灰阶的浪费。从另一个角度来讲,通常一幅图像所包含的过暗和过亮的像素点本来就是少数,有目的有针对性地扩展中间范围灰度而压缩两头的灰度,可增强图像质量,得到更好视觉效果,而图像信息的损失却很小。
1.2 色彩增强
色彩增强的目的是在保证颜色不失真的前提下,有针对性地增加图像的色彩饱和程度,使其看起来更鲜艳生动,层次感更强。
1.2.1 HSI模型简介
在彩色图像处理中,RGB、YCbCr、CMYK等是常用的色彩模型,其算法和相互间的转换很易用硬件实现,但是它们都不能很好适应实际上从人的角度来解释的颜色。
研究表明,从人的角度来观察一个彩色物体时,一般用色调、色饱和度和亮度这3个参量来描述该物体。色调描述纯色的属性,而饱和度给出一种纯色被白光稀释的程度的度量。亮度即图像的明暗程度,是一个主观的描述量。基于这3个参量建立的HSI彩色模型是开发基于彩色描述的图像处理方法的理想工具。下面简单阐述HSI模型的原理。
图1所示是一个RGB彩色空间的立方体模型,边长归一化为1,原点处为黑色,相对的顶点处为白色。连接黑白两点得到灰度轴,这根轴上的饱和度为0,即没有彩色分量。在灰度轴上有相同投影点的点具有相同的亮度,即垂直于灰度轴的平面内的点具有相同的亮度值。
在立方体内任取一点P,它与灰度轴确定一个平面。根据颜色学的理论,所有颜色都是由位于那些颜色定义的三角形内的3种颜色产生的,在这个平面内,三角形的3个顶点分别是黑色、白色和P的颜色,而黑色和白色是不能改变色调的,所以这个平面内的点具有与P点相同的色调,即等色调面。直观地说,越靠近灰度轴的点,颜色越淡,所以色饱和度的定义就是该点与灰度轴的距离:距离越远,饱和度越强;距离越近,饱和度越弱;距离为0则饱和度也为0,这时就完全没有彩色。
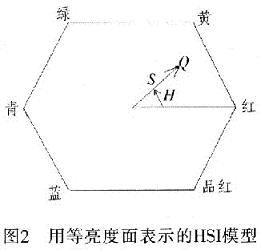
实际上,用垂直于灰度轴的平面内的彩色点轨迹来表示HSI空间(等亮度面)。当平面沿灰度轴上下移动时,由于立方体边界的切割而构成的横截面所决定的边界呈三角形或呈六边形。这里以六边形为例,如图2所示。

由图2看出,三原色是按120°分割的,青、品红和黄被称为二次色,也是按120°分割,一次色与二次色之间相隔60°。图中任给出一点Q,若以红轴作参考,则Q向量与红轴的夹角H决定其色调,而向量长度S决定其饱和度,整个平面在灰度轴上的位置决定了平面内所有点的亮度I。于是得到由RGB到HSI的转换关系:
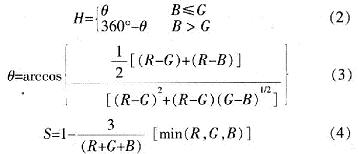

1.2.2 色饱和度增强算法
HSI模型可以方便地对色调和饱和度进行调整,但是其运算比较复杂,很难用硬件来实现。不过根据其原理,可以直接在RGB空间进行色饱和度的调整。这里假设RGB立方体内任一点P(r,g,b),容易求出其在灰度轴上的投影点P*
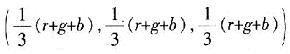
,连接P和P*,这是一条等色调线,如图3所示。
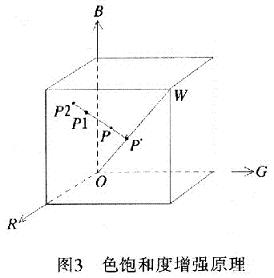
只要在P*P的延长线上找到合适的点(如P1或P2),就可以对P点的饱和度进行增强。由于已知P和P*的坐标,可以求得直线P*P方程:
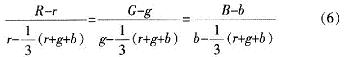
令式(6)的值为t,可求得直线P*P的参数方程:
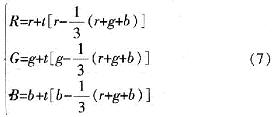
则色饱和度的调整就可通过调整t的取值来实现。当t∈(-1,0)时,得到的点在P*和P之间,饱和度减弱;当t>O时,得到的点在P*P之外,饱和度增强。
2 设计思路
2.1 对比度扩展
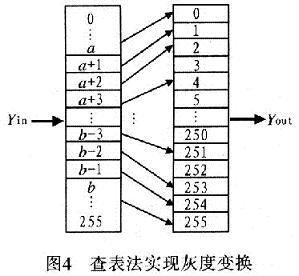
用硬件实现浮点运算效率较低,这里采用查表的方法,在YCbCr空间进行灰度变换,如图4所示。
这里设计一个基于FPGA的实时视频图像处理系统,包含增强对比度扩展和色饱和度两种处理方法,相比于DSP和ASIC方案来说,FPGA在性能和灵活性方面具有绝对优势,应用FPGA设计视频通信系统更普遍。
1 原理和算法
图像增强处理可以在频域和空间域进行,典型的频域方法如直方图增强处理,适合于软件系统实现;而硬件系统更适合于空间域处理,因此本文所述的处理方法都将在空间域进行。
1. 1 对比度扩展
对比度扩展又称灰度变换,其目的是在拓展感兴趣的灰度区间的同时,压缩不感兴趣的灰度区间。最简单有效的方法是线性变换,满足以下关系:
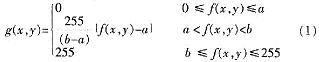
f(x,y)和g(x,y)分别表示输入图像和输出图像的灰度值。经过变换,线性拉伸了在a~b内的灰度值,同时对[0,a]和[b,255]灰度区间进行抑制。从显示设备的角度来说,一般民用级别的显示器都不具备完美表现256灰阶的能力,因此抑制过暗[0,a]和过亮[b,255]的灰度区间而增强中间区域的动态范围,可以避免灰阶的浪费。从另一个角度来讲,通常一幅图像所包含的过暗和过亮的像素点本来就是少数,有目的有针对性地扩展中间范围灰度而压缩两头的灰度,可增强图像质量,得到更好视觉效果,而图像信息的损失却很小。
1.2 色彩增强
色彩增强的目的是在保证颜色不失真的前提下,有针对性地增加图像的色彩饱和程度,使其看起来更鲜艳生动,层次感更强。
1.2.1 HSI模型简介
在彩色图像处理中,RGB、YCbCr、CMYK等是常用的色彩模型,其算法和相互间的转换很易用硬件实现,但是它们都不能很好适应实际上从人的角度来解释的颜色。
研究表明,从人的角度来观察一个彩色物体时,一般用色调、色饱和度和亮度这3个参量来描述该物体。色调描述纯色的属性,而饱和度给出一种纯色被白光稀释的程度的度量。亮度即图像的明暗程度,是一个主观的描述量。基于这3个参量建立的HSI彩色模型是开发基于彩色描述的图像处理方法的理想工具。下面简单阐述HSI模型的原理。
图1所示是一个RGB彩色空间的立方体模型,边长归一化为1,原点处为黑色,相对的顶点处为白色。连接黑白两点得到灰度轴,这根轴上的饱和度为0,即没有彩色分量。在灰度轴上有相同投影点的点具有相同的亮度,即垂直于灰度轴的平面内的点具有相同的亮度值。

在立方体内任取一点P,它与灰度轴确定一个平面。根据颜色学的理论,所有颜色都是由位于那些颜色定义的三角形内的3种颜色产生的,在这个平面内,三角形的3个顶点分别是黑色、白色和P的颜色,而黑色和白色是不能改变色调的,所以这个平面内的点具有与P点相同的色调,即等色调面。直观地说,越靠近灰度轴的点,颜色越淡,所以色饱和度的定义就是该点与灰度轴的距离:距离越远,饱和度越强;距离越近,饱和度越弱;距离为0则饱和度也为0,这时就完全没有彩色。
实际上,用垂直于灰度轴的平面内的彩色点轨迹来表示HSI空间(等亮度面)。当平面沿灰度轴上下移动时,由于立方体边界的切割而构成的横截面所决定的边界呈三角形或呈六边形。这里以六边形为例,如图2所示。

由图2看出,三原色是按120°分割的,青、品红和黄被称为二次色,也是按120°分割,一次色与二次色之间相隔60°。图中任给出一点Q,若以红轴作参考,则Q向量与红轴的夹角H决定其色调,而向量长度S决定其饱和度,整个平面在灰度轴上的位置决定了平面内所有点的亮度I。于是得到由RGB到HSI的转换关系:
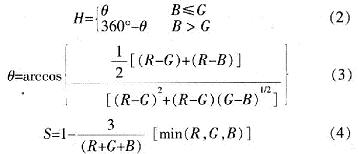

1.2.2 色饱和度增强算法
HSI模型可以方便地对色调和饱和度进行调整,但是其运算比较复杂,很难用硬件来实现。不过根据其原理,可以直接在RGB空间进行色饱和度的调整。这里假设RGB立方体内任一点P(r,g,b),容易求出其在灰度轴上的投影点P*
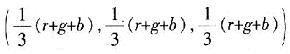
,连接P和P*,这是一条等色调线,如图3所示。

只要在P*P的延长线上找到合适的点(如P1或P2),就可以对P点的饱和度进行增强。由于已知P和P*的坐标,可以求得直线P*P方程:
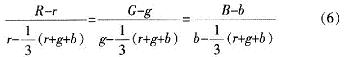
令式(6)的值为t,可求得直线P*P的参数方程:
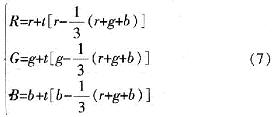
则色饱和度的调整就可通过调整t的取值来实现。当t∈(-1,0)时,得到的点在P*和P之间,饱和度减弱;当t>O时,得到的点在P*P之外,饱和度增强。
2 设计思路
2.1 对比度扩展
用硬件实现浮点运算效率较低,这里采用查表的方法,在YCbCr空间进行灰度变换,如图4所示。

电路 显示器 FPGA DSP ModelSim 仿真 相关文章:
- 基于Virtex-5 FPGA设计Gbps无线通信基站(05-12)
- 基于FPGA的DVI/HDMI接口实现(05-13)
- 基于ARM的嵌入式系统中从串配置FPGA的实现(06-09)
- 基于PLB总线的H.264整数变换量化软核的设计(03-20)
- FPGA按键模式的研究与设计(03-24)
- 周立功:如何兼顾学习ARM与FPGA(05-23)
