基于FPGA的等位移多点采样硬币识别研究
时间:11-08
来源:互联网
点击:
硬币的识别分为两个方面:对于硬币币值的准确检测;对于真币、伪币的准确鉴别。由于硬币的复杂性,长期以来,对于硬币的准确识别都难以很好的解决。目前,无论是国外还是国内,通常的解决方法都是基于单片机的电涡流检测法。本文在电涡流检测的基础上,利用FPGA的快速处理特性和高可靠特性,对硬币的厚度、直径、材质、电导率、磁导率等进行了准确的检测,以便准确地识别硬币。
1 电涡流反射式互补检测传感器原理
电涡流检测是建立在电磁感应原理基础之上的一种无损检测方法,它适用于导电材料,如果把一块导体置于交变磁场之中,在导体中就有感应电流存在,即产生涡流,由于导体自身各种因素(如电导率、磁导率、形状、尺寸和缺陷等)的变化会导致感应电流的变化,利用这种现象判知导体性质、状态的检测方法,叫作电涡流检测法。
在电涡流检测中,是靠检测线圈来建立交变磁场的;把能量传递给被检导体,同时又通过涡流建立的交变磁场获得被检测导体中的质量信息。
在本硬币识别器中,采用探头式线圈,由于硬币在币道中滚动时,其在径向位置会产生微小的抖动,为了消除这种抖动带来的影响,在币道两边都安装有检测线圈,进行探头互补式检测。如图1所示。
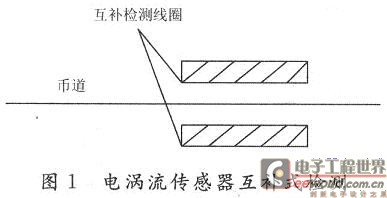
检测线圈和检测线路组成一个振荡器,当硬币通过币道时,线圈的电感会发生变化,引起检测电路振荡频率发生变化。通过FPGA对振荡频率进行检测,以正确识别硬币。
2 基于FPGA的等位移多点采样原理
硬币通过检测线圈时,会引起振荡频率发生变化,传统的检测方法通常是检测变化的振荡频率的极值,即最大值。但这种检测方法只有一个采样点,识别伪币能力不强。也有人采用每过一段相同的时间取一次采样点,通过多采样点提高识别效果。但是,当硬币通过币道时,由于投币力量、初始速度以及硬币边缘的光滑程度、硬币的重量等的区别,并不是每一种硬币通过检测线圈时的速度都是一致的;同一种、甚至同一个硬币,也并不是每次通过检测线圈时的速度都是一致的。所以,若采取等时间间隔取样,就会造成取样时,硬币和检测线圈的物理相对位置不一样,引起检测结果不一样。这不仅会引起对伪币可靠识别的准确性,也会影响对真币的币值检测及真币识别的可靠性,甚至把真币当成伪币来识别。正是由于这些问题,在实际的硬币识别器产品中,通常采用的是只采取一个采样点,即极值采样法,但这种单点采样法由于只在硬币通过币道的某一瞬间获取硬币的参数信息,有很大的局限性,识别伪币能力不强。
在该设计中,采取等位移多点取样法,完全克服了以上方法的缺点,具有很高的识币能力。同时,还能对硬币的直径进行检测。
由于采样时间和采样间隔都很短,对系统的高速性和可靠性有较高的要求,用传统的单片机难以满足要求,在该设计中,通过FPGA完成对数据的高速采样和处理。
2.1 系统原理
图2为系统原理框图。在币道的不同位置安装有几个光电传感器,通过基于FPGA的脉冲宽度测量,可检测得到硬币通过币道中光电传感器之问距离的间隔时间。通过FPGA的高速数据处理,可得到硬币的直径、硬币通过币道时的加速度,并得到硬币进行等位移多点采样的采样时刻。当硬币通过检测线圈时,就进行基于 FPGA的多倍周期同步测频。再由FPGA对数据进行高速处理,得到硬币的特征参数,再把该特征参数和E2PROM中的硬币特征值进行比较,就可以判别硬币的币值和真伪。
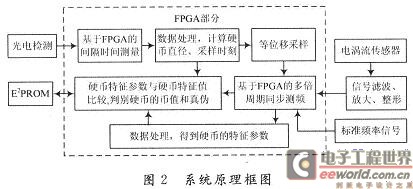
2.2 基于FPGA的间隔时间测量
图3为基于FPGA的间隔时间测量原理示意图,A,B,C三点为光电检测点。当硬币通过光电检测点时,光电检测电路的输出由低电平跳变为高电平。图4为硬币通过币道时A,B,C三个光电传感器的输出波形。
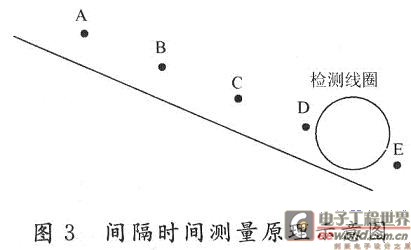
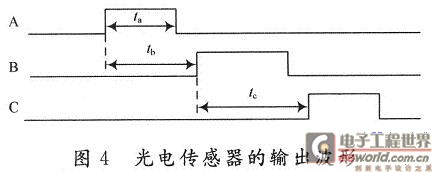
图4中,ta为硬币前沿通过A点到硬币后沿经过A点的间隔时间;tb为硬币前沿通过A点到硬币前沿通过B点的间隔时间;tc为硬币前沿通过B点到硬币前沿通过C点的间隔时间。
光电传感器的输出接到FPGA,由FPGA对标准频率信号进行计数,不难测得硬币通过币道时的间隔时间ta,tb,tc。在本设计中,FPGA的时钟频率为100 MHz,即标准频率信号为100 MHz。经过实际检测,ta,tb,tc的最小时间为0.01 s,则可估算出最大测量误差为:
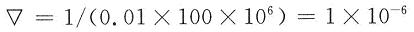
可见有足够高的精确度。
2.3 硬币直径检测
通过光电传感器实现硬币直径及通过币道的加速度的检测。如图3,在币道的A点、B点和C点分别安装光电收发器。AB点和BC点的距离相等且为s。
硬币通过币道时做匀加速度运动,设加速度为a,下面通过由FPGA高速检测得到的ta,tb,tc以及光电传感器之间的距离s来求加速度a,并求出硬币的直径d。
设硬币的前沿通过A点,B点,C点的速度分别为vA,vB,vc,则有:
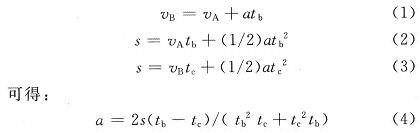
由此可计算出硬币通过币道时的加速度a。设光电传感器A距离币道底部的垂直距离为h;光电传感器A检测点扫过硬币的长度为l。图5为硬币的半径r和h,l的关系图。由图5可得如下公式:
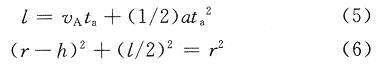
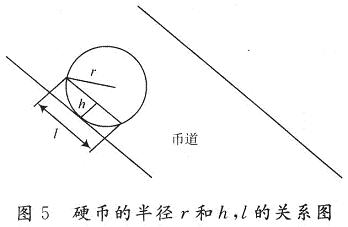
硬币的直径为d=2r,由式(1)~式(6)可得:

式中:h和s是已知的;ta,tb,tc可通过FPGA检测得到。
由此公式,就可通过测量硬币通过的时间ta,tb,tc并计算得到硬币的直径d。
2.4 等距离多点采样
见图3,D,E点位置设在检测线圈的边缘,CD间的距离为s。当硬币前沿通过D点时,开始采样;当硬币后沿通过E点时,停止采样。为了充分地采集硬币在各个位置的参数信息,采样点应足够多。在本设计中,沿硬币滚动的方向每间隔0.1 mm位移采样一次。
检测线圈和检测电路组成振荡器,振荡频率既不能太高,也不能太低。在本设计中,振荡频率为200 kHz(此频率指硬币未通过线圈时的振荡频率)。经实际测试,硬币通过检测线圈时的速度范围为0.1~0.5 m/s。可见,硬币通过币道时的速度有较大的变化范围,同一硬币多次投币时,通过检测线圈同一点(比如:A点)的速度也有区别。为了实现每次投币多点采样时,检测线圈和硬币的相对位置都一样,就必须采取等位移多点采样。当硬币的前沿通过D点时开始采样,以硬币前沿通过D点的时刻作为采样时间的零起始时刻,每过0.1 mm采样一次。首先,需要计算出通过每一个0.1 mm位移所需要的时间t1,t2,t3,…。由于速度越来越快,必定有t1,>t2>t3>…,再每隔t1,t2,t3,…时间检测采样一次。图6为采样过程示意图,tS为采样时间。
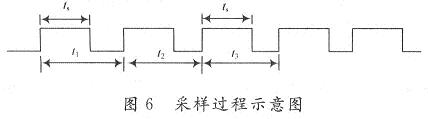
由于硬币在币道中做匀加速度直线运动,设硬币的前沿通过D点时的速度为vD,则有:
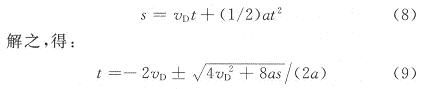
令s为0.1 mm,0.2 mm,0.3 mm,…,设需要的时间分别为t0.1,t0.2,t0.3,…。由2.3所述方法可求得a和vD,则通过求解一元二次方程可得到t0.1,t0.2, t0.3,…,若以硬币通过D点作为零时间参考点,则在t0.1,t0.2,t0.3,…采样即可得到正确的等位移多采样值。有:t1=t0.2-t0. 1,t2=t0.3-t0.2,…。
当硬币后沿通过E点时,停止采样,D点和E点的沿币道方向的距离为y,设通过E点的时刻为tE,则有:
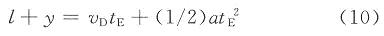
由此即可计算出tE,即为硬币通过币道时最后一个采样点。
根据式(9),要求得t,涉及到开方运算。开方运算的算法主要有Newton-Raphson算法、SRT-Redun-ant算法和Non-Redudant算法。这三种算法可以得到开方运算的近似结果。关于上述三种算法的介绍参见参考文献[1—3]。
为了有足够高的检测精度,要求t精确到1μs。另外,由于硬币由C点到D点的最小时间为0.3 ms,所以必须在0.3 ms内完成上述的算法。通过FPGA不难实现这些要求,但是若采用单片机来实现就有一定的难度,如:若用51单片机,频率12 MHz来实现,则机器周期就是1μs,要实现上述算法是不可能的。所以在该设计中采用FPGA实现。
2.5 基于FPGA的多倍周期同步测频法
在该设计中,检测线圈为电涡流反射式互补检测,准确地测试出其输出频率是很重要的。对于频率的测试,有测频法、测周期法,但测量精度都不够高,在该设计中,两种测试方法误差都比较大,所以采用等精度多倍周期同步测频法,可达到较高的精度。
由于硬币通过检测线圈时的速度范围为:0.1~0.5 m/s,要求每隔0.1 mm距离采样一次,则采样的时间间隔范围为0.2~1ms。为了保证采样的快速和准确性,采样时间不能超过0.2 ms,本设计采样时间取0.1 ms。
该设计中,FPGA的频率为100 MHz,由检测线圈及检测电路组成的振荡器频率为200 kHz(此频率指硬币未通过线圈时的振荡频率)。
所谓测频法,就是先给定一个闸门时间,在此闸门时间内,对被测频率信号计数,由此即可计算出被测信号的频率。在本设计中,闸门时间为0.1 ms,被测信号频率为200 kHz左右,若用测频法,则测量误差为:
1/(0.1×10-3×200×103)=5%
所谓测周期法,就是在被测频率信号的一个周期内,对参考频率信号进行计数,由此即可计算出被测信号的周期,在本设计中,参考频率信号为100 MHz,被测信号频率为200 kHz左右,若用测周期法,则测量误差为:
(200×103)/(100×106)=0.2%
由此可见,都有较大的误差,下面用等精度多倍周期同步测频法,既可以在振荡频率变化的情况下保持精度的一致,又可以减少测量误差,提高测试精度。
设被测信号频率为fx,计数器CT1对fx进行计数;参考信号频率为fr,计数器CT2对fr进行计数。
CT1的闸门开放时间完全与fx的m个周期同步。闸门开放时间T1=mtx。在fx的第一个上升沿和第m+1个上升沿之间的mtx时间间隔内,允许CT2对fr计数,计数值记为N。上述测频的时序图如图7所示。
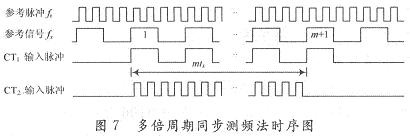
fx的计算公式如下:
fx=m/Nfr
根据误差传递公式,有:
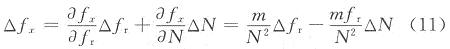
式中:△fx,△fr,△N为绝对误差。相对误差δ=±(△fx/fx),由于fr由晶体振荡器输出,其稳定度较高,所以△fr非常小,可忽略不计。△N极限是±1,故测量误差δ为:
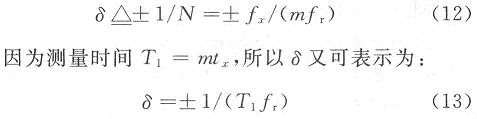
由式(13)可以看出,测量误差与被测信号的频率大小无关,仅与闸门时间和标准频率时间有关。标准频率越高,闸门时间越长,测量误差越小。
在本设计中,为了保证测量的速度,闸门时间比较短,在闸门时间不变的情况下,标准频率越高,误差越小。
为了提高测量频率的精度,必须采用较高频率的标准信号。在传统的硬币识别器设计中,多采用单片机测量频率,但由于单片机受本身的时钟频率和若干指令运算的限制,难以得到较高的标准频率信号,无法满足高速、高精度的测量要求。采用高速、高精度、高可靠性的现场可编程阵列FPGA为实现高速、高精度的测频提供了保证。
在本设计中,fr=100 MHz,T1=0.1 ms,则相对测量误差δ为:
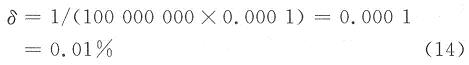
误差远小于测频法和测周期法误差。这就解决了瞬时、快速采样的测量精度问题。
若用传统的单片机等精度多倍同步测频方案,假设用常用的MCS-51单片机,设时钟频率为12 MHz,机器周期为1 MHz,则误差为:
δ1=1/(1 000 000×0.000 1)=0.01=1%(15)
可见,用传统的单片机采集频率数据,误差太大,难以满足高精度测量的要求。
正是出于提高测量精度的考虑,在本设计里用了FPGA来完成频率数据的采集工作。
1 电涡流反射式互补检测传感器原理
电涡流检测是建立在电磁感应原理基础之上的一种无损检测方法,它适用于导电材料,如果把一块导体置于交变磁场之中,在导体中就有感应电流存在,即产生涡流,由于导体自身各种因素(如电导率、磁导率、形状、尺寸和缺陷等)的变化会导致感应电流的变化,利用这种现象判知导体性质、状态的检测方法,叫作电涡流检测法。
在电涡流检测中,是靠检测线圈来建立交变磁场的;把能量传递给被检导体,同时又通过涡流建立的交变磁场获得被检测导体中的质量信息。
在本硬币识别器中,采用探头式线圈,由于硬币在币道中滚动时,其在径向位置会产生微小的抖动,为了消除这种抖动带来的影响,在币道两边都安装有检测线圈,进行探头互补式检测。如图1所示。

检测线圈和检测线路组成一个振荡器,当硬币通过币道时,线圈的电感会发生变化,引起检测电路振荡频率发生变化。通过FPGA对振荡频率进行检测,以正确识别硬币。
2 基于FPGA的等位移多点采样原理
硬币通过检测线圈时,会引起振荡频率发生变化,传统的检测方法通常是检测变化的振荡频率的极值,即最大值。但这种检测方法只有一个采样点,识别伪币能力不强。也有人采用每过一段相同的时间取一次采样点,通过多采样点提高识别效果。但是,当硬币通过币道时,由于投币力量、初始速度以及硬币边缘的光滑程度、硬币的重量等的区别,并不是每一种硬币通过检测线圈时的速度都是一致的;同一种、甚至同一个硬币,也并不是每次通过检测线圈时的速度都是一致的。所以,若采取等时间间隔取样,就会造成取样时,硬币和检测线圈的物理相对位置不一样,引起检测结果不一样。这不仅会引起对伪币可靠识别的准确性,也会影响对真币的币值检测及真币识别的可靠性,甚至把真币当成伪币来识别。正是由于这些问题,在实际的硬币识别器产品中,通常采用的是只采取一个采样点,即极值采样法,但这种单点采样法由于只在硬币通过币道的某一瞬间获取硬币的参数信息,有很大的局限性,识别伪币能力不强。
在该设计中,采取等位移多点取样法,完全克服了以上方法的缺点,具有很高的识币能力。同时,还能对硬币的直径进行检测。
由于采样时间和采样间隔都很短,对系统的高速性和可靠性有较高的要求,用传统的单片机难以满足要求,在该设计中,通过FPGA完成对数据的高速采样和处理。
2.1 系统原理
图2为系统原理框图。在币道的不同位置安装有几个光电传感器,通过基于FPGA的脉冲宽度测量,可检测得到硬币通过币道中光电传感器之问距离的间隔时间。通过FPGA的高速数据处理,可得到硬币的直径、硬币通过币道时的加速度,并得到硬币进行等位移多点采样的采样时刻。当硬币通过检测线圈时,就进行基于 FPGA的多倍周期同步测频。再由FPGA对数据进行高速处理,得到硬币的特征参数,再把该特征参数和E2PROM中的硬币特征值进行比较,就可以判别硬币的币值和真伪。

2.2 基于FPGA的间隔时间测量
图3为基于FPGA的间隔时间测量原理示意图,A,B,C三点为光电检测点。当硬币通过光电检测点时,光电检测电路的输出由低电平跳变为高电平。图4为硬币通过币道时A,B,C三个光电传感器的输出波形。


图4中,ta为硬币前沿通过A点到硬币后沿经过A点的间隔时间;tb为硬币前沿通过A点到硬币前沿通过B点的间隔时间;tc为硬币前沿通过B点到硬币前沿通过C点的间隔时间。
光电传感器的输出接到FPGA,由FPGA对标准频率信号进行计数,不难测得硬币通过币道时的间隔时间ta,tb,tc。在本设计中,FPGA的时钟频率为100 MHz,即标准频率信号为100 MHz。经过实际检测,ta,tb,tc的最小时间为0.01 s,则可估算出最大测量误差为:
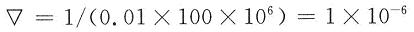
可见有足够高的精确度。
2.3 硬币直径检测
通过光电传感器实现硬币直径及通过币道的加速度的检测。如图3,在币道的A点、B点和C点分别安装光电收发器。AB点和BC点的距离相等且为s。
硬币通过币道时做匀加速度运动,设加速度为a,下面通过由FPGA高速检测得到的ta,tb,tc以及光电传感器之间的距离s来求加速度a,并求出硬币的直径d。
设硬币的前沿通过A点,B点,C点的速度分别为vA,vB,vc,则有:
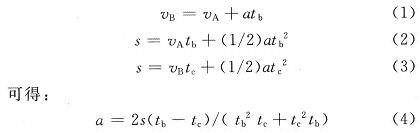
由此可计算出硬币通过币道时的加速度a。设光电传感器A距离币道底部的垂直距离为h;光电传感器A检测点扫过硬币的长度为l。图5为硬币的半径r和h,l的关系图。由图5可得如下公式:
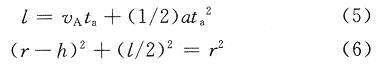

硬币的直径为d=2r,由式(1)~式(6)可得:

式中:h和s是已知的;ta,tb,tc可通过FPGA检测得到。
由此公式,就可通过测量硬币通过的时间ta,tb,tc并计算得到硬币的直径d。
2.4 等距离多点采样
见图3,D,E点位置设在检测线圈的边缘,CD间的距离为s。当硬币前沿通过D点时,开始采样;当硬币后沿通过E点时,停止采样。为了充分地采集硬币在各个位置的参数信息,采样点应足够多。在本设计中,沿硬币滚动的方向每间隔0.1 mm位移采样一次。
检测线圈和检测电路组成振荡器,振荡频率既不能太高,也不能太低。在本设计中,振荡频率为200 kHz(此频率指硬币未通过线圈时的振荡频率)。经实际测试,硬币通过检测线圈时的速度范围为0.1~0.5 m/s。可见,硬币通过币道时的速度有较大的变化范围,同一硬币多次投币时,通过检测线圈同一点(比如:A点)的速度也有区别。为了实现每次投币多点采样时,检测线圈和硬币的相对位置都一样,就必须采取等位移多点采样。当硬币的前沿通过D点时开始采样,以硬币前沿通过D点的时刻作为采样时间的零起始时刻,每过0.1 mm采样一次。首先,需要计算出通过每一个0.1 mm位移所需要的时间t1,t2,t3,…。由于速度越来越快,必定有t1,>t2>t3>…,再每隔t1,t2,t3,…时间检测采样一次。图6为采样过程示意图,tS为采样时间。

由于硬币在币道中做匀加速度直线运动,设硬币的前沿通过D点时的速度为vD,则有:
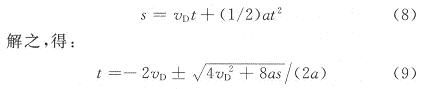
令s为0.1 mm,0.2 mm,0.3 mm,…,设需要的时间分别为t0.1,t0.2,t0.3,…。由2.3所述方法可求得a和vD,则通过求解一元二次方程可得到t0.1,t0.2, t0.3,…,若以硬币通过D点作为零时间参考点,则在t0.1,t0.2,t0.3,…采样即可得到正确的等位移多采样值。有:t1=t0.2-t0. 1,t2=t0.3-t0.2,…。
当硬币后沿通过E点时,停止采样,D点和E点的沿币道方向的距离为y,设通过E点的时刻为tE,则有:
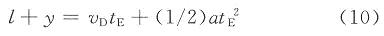
由此即可计算出tE,即为硬币通过币道时最后一个采样点。
根据式(9),要求得t,涉及到开方运算。开方运算的算法主要有Newton-Raphson算法、SRT-Redun-ant算法和Non-Redudant算法。这三种算法可以得到开方运算的近似结果。关于上述三种算法的介绍参见参考文献[1—3]。
为了有足够高的检测精度,要求t精确到1μs。另外,由于硬币由C点到D点的最小时间为0.3 ms,所以必须在0.3 ms内完成上述的算法。通过FPGA不难实现这些要求,但是若采用单片机来实现就有一定的难度,如:若用51单片机,频率12 MHz来实现,则机器周期就是1μs,要实现上述算法是不可能的。所以在该设计中采用FPGA实现。
2.5 基于FPGA的多倍周期同步测频法
在该设计中,检测线圈为电涡流反射式互补检测,准确地测试出其输出频率是很重要的。对于频率的测试,有测频法、测周期法,但测量精度都不够高,在该设计中,两种测试方法误差都比较大,所以采用等精度多倍周期同步测频法,可达到较高的精度。
由于硬币通过检测线圈时的速度范围为:0.1~0.5 m/s,要求每隔0.1 mm距离采样一次,则采样的时间间隔范围为0.2~1ms。为了保证采样的快速和准确性,采样时间不能超过0.2 ms,本设计采样时间取0.1 ms。
该设计中,FPGA的频率为100 MHz,由检测线圈及检测电路组成的振荡器频率为200 kHz(此频率指硬币未通过线圈时的振荡频率)。
所谓测频法,就是先给定一个闸门时间,在此闸门时间内,对被测频率信号计数,由此即可计算出被测信号的频率。在本设计中,闸门时间为0.1 ms,被测信号频率为200 kHz左右,若用测频法,则测量误差为:
1/(0.1×10-3×200×103)=5%
所谓测周期法,就是在被测频率信号的一个周期内,对参考频率信号进行计数,由此即可计算出被测信号的周期,在本设计中,参考频率信号为100 MHz,被测信号频率为200 kHz左右,若用测周期法,则测量误差为:
(200×103)/(100×106)=0.2%
由此可见,都有较大的误差,下面用等精度多倍周期同步测频法,既可以在振荡频率变化的情况下保持精度的一致,又可以减少测量误差,提高测试精度。
设被测信号频率为fx,计数器CT1对fx进行计数;参考信号频率为fr,计数器CT2对fr进行计数。
CT1的闸门开放时间完全与fx的m个周期同步。闸门开放时间T1=mtx。在fx的第一个上升沿和第m+1个上升沿之间的mtx时间间隔内,允许CT2对fr计数,计数值记为N。上述测频的时序图如图7所示。

fx的计算公式如下:
fx=m/Nfr
根据误差传递公式,有:
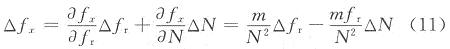
式中:△fx,△fr,△N为绝对误差。相对误差δ=±(△fx/fx),由于fr由晶体振荡器输出,其稳定度较高,所以△fr非常小,可忽略不计。△N极限是±1,故测量误差δ为:
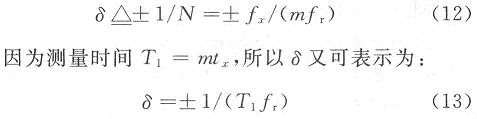
由式(13)可以看出,测量误差与被测信号的频率大小无关,仅与闸门时间和标准频率时间有关。标准频率越高,闸门时间越长,测量误差越小。
在本设计中,为了保证测量的速度,闸门时间比较短,在闸门时间不变的情况下,标准频率越高,误差越小。
为了提高测量频率的精度,必须采用较高频率的标准信号。在传统的硬币识别器设计中,多采用单片机测量频率,但由于单片机受本身的时钟频率和若干指令运算的限制,难以得到较高的标准频率信号,无法满足高速、高精度的测量要求。采用高速、高精度、高可靠性的现场可编程阵列FPGA为实现高速、高精度的测频提供了保证。
在本设计中,fr=100 MHz,T1=0.1 ms,则相对测量误差δ为:
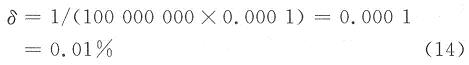
误差远小于测频法和测周期法误差。这就解决了瞬时、快速采样的测量精度问题。
若用传统的单片机等精度多倍同步测频方案,假设用常用的MCS-51单片机,设时钟频率为12 MHz,机器周期为1 MHz,则误差为:
δ1=1/(1 000 000×0.000 1)=0.01=1%(15)
可见,用传统的单片机采集频率数据,误差太大,难以满足高精度测量的要求。
正是出于提高测量精度的考虑,在本设计里用了FPGA来完成频率数据的采集工作。
单片机 FPGA 传感器 电流 振荡器 电感 电路 收发器 51单片机 相关文章:
- 采用EEPROM对大容量FPGA芯片数据实现串行加载(03-18)
- 周立功:如何兼顾学习ARM与FPGA(05-23)
- 初学者如何学习FPGA(08-06)
- 为何、如何学习FPGA(05-23)
- FPGA作为协处理器在实时系统中的应用(04-08)
- 我的FPGA学习历程(05-23)
