分布式算法和FPGA实现基带信号成形的研究
时间:11-08
来源:互联网
点击:
根据Nyquist第一准则,基带信号成形能够消除码间串扰的影响。随着超高速数字集成电路的发展,成形滤波器已经由过去的基带频域模拟成形滤波器变成现在的基带时域数字成形滤波器。与基带模拟成形滤波器相比,基带数字成形滤波器具有高精度、高可靠性和高灵活性等优点;同时还具有便于大规模集成、易于实现线性相位等特点。实现其带数字成形的方法很多,与传统算法相比,分布式算法可以极大地减少硬件电路的规模,提高电路的执行速度。本文采用基于分布式算法思想的时域成形方法来实现基带信号成形。
1 分布式算法的基本原理
一个线性时不变网络的输出可以用下式表示:
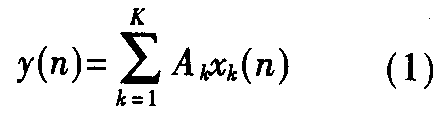
其中,y(n)为第n时刻网络的输出;xk(n)为第n时刻的第k个输入变量;Ak为第k个输入变量的权值。在线性时不变系统中,对于所有n时刻,Ak都是常量。如果该网络表示为滤波器,常量Ak即为滤波器抽头系数,变量xk为单一数据源的抽样数据。仔细观察(1)式可以看出,输出单个y(n)需要将k个乘积累加,这种累加可以通过查找表来实现,大大提高了运算的效率。为了使乘法之后的数据宽度不至于展宽,先把数据源数据格式规定为浮点数2的补码形式。需要注意的是,常量Ak不一定要进行格式转换来匹配输入数据的格式,它可以根据要求的精度进行定义。变量xk可用下式表示:
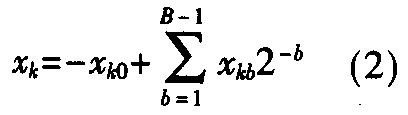
式中,xkb为二进制数,即取值为0或1;xk0为符号位,“1”表示数据为负,“0”表示数据为正。式中,时间参数“n”已经被省略掉,因为在以下的推导中与时间参数无关。将(2)式代入(1)式中,得:

将(3)式展开,得:

从(4)式可以看出,每个方括号中进行的是输入变量的某一个数据位和所有常量A1~Ak的每一位进行位相“与”然后求和,而指数部分则说明了求和结果的位加权,这种加权可以通过移位来实现。而方括号中的计算可以通过建立查找表来实现,具体的操作通过所有输入变量的同一位进行寻址来完成。通过(4)式,(1)式就可以用加法、减少和二进制除法来计算了,这样就避免了频繁地使用乘示器,从而节约了系统的资源,并且大大缩短了运算时间。
2 时域成形的原理
(4)式中的查找表方法中以缩短运算的时间,但是二进制除法还是会消耗掉大量的系统时钟。因为要设计的是基带信号成形滤波器,所以可以通过直接在时域上成形的方法来完成。
如果输入为二进制双极性数据,采用升余弦滚降滤波器进行脉冲成形,其系统函数为:

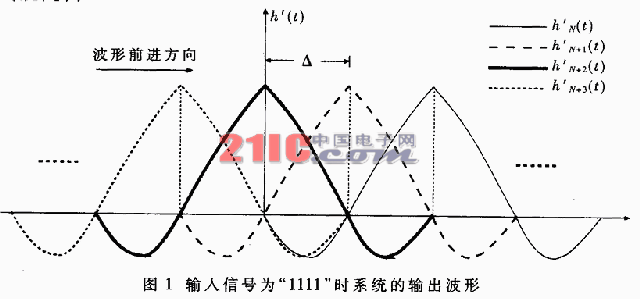
若取截短长度为输入信号元宽度的4倍,则当输入信号为“1111”时,系统的输出波形如图1所示。
图中,h‘(t)为h(t)的截短。由图1可知,只需要求出Δ时间段的波形叠加值,依次输出,就可以得到输入信号的成形波形。若在段内抽样8点,则每个样点有2 4个可能值,共有2 4 x 8=128个数据。将这128个数据存入查找表中,用连续四个输入信号进行寻址,就可以不必计算二进制除法,从而提高系统的运算速度。其硬件原理图如图2所示。
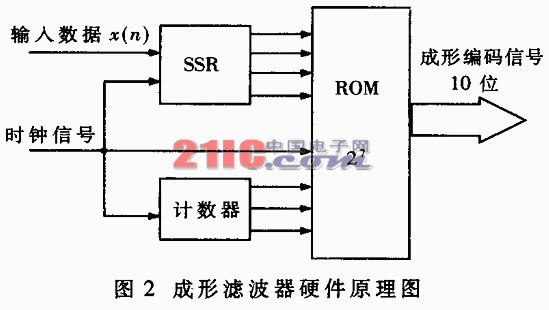
图中,SSR是一个四位移位寄存器,数据串行输入,并行输出,初始状态预置为“0000”,每一时钟信号读入一位数据,同时串行移位;计数器为8位,每次时钟从000计数至111;ROM的宽度为7位,存储2 7个数据,对应各个样点的数值,每次时钟到来时,输出8个10比特宽的数据。
3 用FPGA实现
由图2可知,系统主要由移位寄存器、计数器和查找表组成,其中查找表(ROM)对系统运算速度的影响最大。如果直接用宽度为7的查找表进行寻址的话,最长的寻址路径需要2 7个系统时钟,这样损失太大。所以考虑用寻址宽度小的查找表。假定系统输入数据的码速度为4.352Mbps,滤波器的滚降系数α=0.35,则用FPGA可实现成形滤波器。
3.1 输入单元
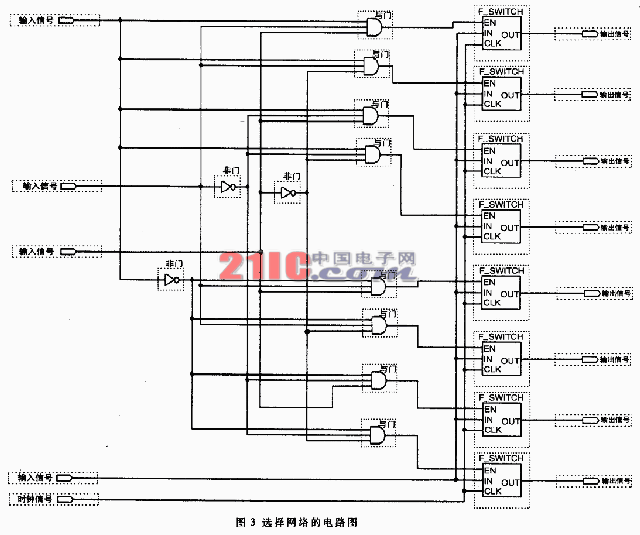
输入单元由移位寄存器和选择网络组成。移位寄存器是由四个带异步复位端的D触发器级连而成,数据串行输入,并行输出,共用同一个时钟和异步复位信号,其作用是将输入数据读入查找表中。选择网络是为了减小查找表的寻址宽度,根据前三个输入数据的值来选择对应的查找表。选择网络的电路图如图3所示。
图中的“F_SWITCH”模块是一个开关电路,当使能端为高电平时,将输入端的数据输出,否则输出端为高阻态。根据图3的原理,当前三个输入信号为100时,选中第5个开关。这样,只要将第5个开关选通的查找表中数据依次输出,就可以得到成形信号。这时查找表的寻址宽度为3位,大大节约了寻址时间。查找表寻址方式的电路图如图4所示。
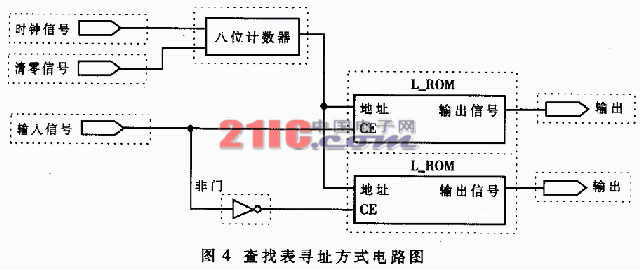
在图4中,计数器的作用是在第四位数据到来时,激励查找表将其存储的8个数据依次输出。L_ROM是寻址宽度为3位的查找表。
3.2 查找表
在图1中的Δ段内抽样8点,且滤波器为升余弦滚降滤波器,则有下式成立:
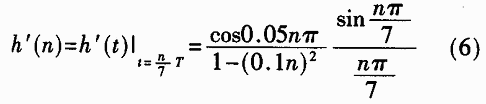
所以这8个样点值可由下式表示:
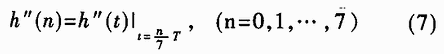
对(7)式进行计算,列出所有可能的样点值,如表1所示。
表1 成形滤波器的样点值
1 分布式算法的基本原理
一个线性时不变网络的输出可以用下式表示:
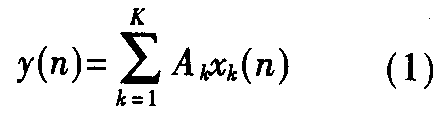
其中,y(n)为第n时刻网络的输出;xk(n)为第n时刻的第k个输入变量;Ak为第k个输入变量的权值。在线性时不变系统中,对于所有n时刻,Ak都是常量。如果该网络表示为滤波器,常量Ak即为滤波器抽头系数,变量xk为单一数据源的抽样数据。仔细观察(1)式可以看出,输出单个y(n)需要将k个乘积累加,这种累加可以通过查找表来实现,大大提高了运算的效率。为了使乘法之后的数据宽度不至于展宽,先把数据源数据格式规定为浮点数2的补码形式。需要注意的是,常量Ak不一定要进行格式转换来匹配输入数据的格式,它可以根据要求的精度进行定义。变量xk可用下式表示:
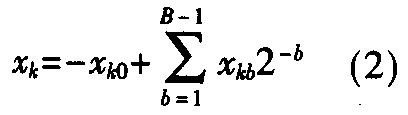
式中,xkb为二进制数,即取值为0或1;xk0为符号位,“1”表示数据为负,“0”表示数据为正。式中,时间参数“n”已经被省略掉,因为在以下的推导中与时间参数无关。将(2)式代入(1)式中,得:

将(3)式展开,得:

从(4)式可以看出,每个方括号中进行的是输入变量的某一个数据位和所有常量A1~Ak的每一位进行位相“与”然后求和,而指数部分则说明了求和结果的位加权,这种加权可以通过移位来实现。而方括号中的计算可以通过建立查找表来实现,具体的操作通过所有输入变量的同一位进行寻址来完成。通过(4)式,(1)式就可以用加法、减少和二进制除法来计算了,这样就避免了频繁地使用乘示器,从而节约了系统的资源,并且大大缩短了运算时间。

2 时域成形的原理
(4)式中的查找表方法中以缩短运算的时间,但是二进制除法还是会消耗掉大量的系统时钟。因为要设计的是基带信号成形滤波器,所以可以通过直接在时域上成形的方法来完成。
如果输入为二进制双极性数据,采用升余弦滚降滤波器进行脉冲成形,其系统函数为:

若取截短长度为输入信号元宽度的4倍,则当输入信号为“1111”时,系统的输出波形如图1所示。
图中,h‘(t)为h(t)的截短。由图1可知,只需要求出Δ时间段的波形叠加值,依次输出,就可以得到输入信号的成形波形。若在段内抽样8点,则每个样点有2 4个可能值,共有2 4 x 8=128个数据。将这128个数据存入查找表中,用连续四个输入信号进行寻址,就可以不必计算二进制除法,从而提高系统的运算速度。其硬件原理图如图2所示。

图中,SSR是一个四位移位寄存器,数据串行输入,并行输出,初始状态预置为“0000”,每一时钟信号读入一位数据,同时串行移位;计数器为8位,每次时钟从000计数至111;ROM的宽度为7位,存储2 7个数据,对应各个样点的数值,每次时钟到来时,输出8个10比特宽的数据。
3 用FPGA实现
由图2可知,系统主要由移位寄存器、计数器和查找表组成,其中查找表(ROM)对系统运算速度的影响最大。如果直接用宽度为7的查找表进行寻址的话,最长的寻址路径需要2 7个系统时钟,这样损失太大。所以考虑用寻址宽度小的查找表。假定系统输入数据的码速度为4.352Mbps,滤波器的滚降系数α=0.35,则用FPGA可实现成形滤波器。

3.1 输入单元
输入单元由移位寄存器和选择网络组成。移位寄存器是由四个带异步复位端的D触发器级连而成,数据串行输入,并行输出,共用同一个时钟和异步复位信号,其作用是将输入数据读入查找表中。选择网络是为了减小查找表的寻址宽度,根据前三个输入数据的值来选择对应的查找表。选择网络的电路图如图3所示。
图中的“F_SWITCH”模块是一个开关电路,当使能端为高电平时,将输入端的数据输出,否则输出端为高阻态。根据图3的原理,当前三个输入信号为100时,选中第5个开关。这样,只要将第5个开关选通的查找表中数据依次输出,就可以得到成形信号。这时查找表的寻址宽度为3位,大大节约了寻址时间。查找表寻址方式的电路图如图4所示。

在图4中,计数器的作用是在第四位数据到来时,激励查找表将其存储的8个数据依次输出。L_ROM是寻址宽度为3位的查找表。
3.2 查找表
在图1中的Δ段内抽样8点,且滤波器为升余弦滚降滤波器,则有下式成立:
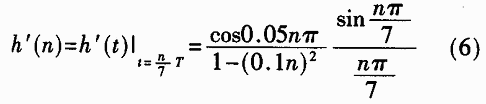
所以这8个样点值可由下式表示:
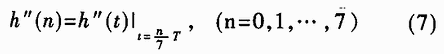
对(7)式进行计算,列出所有可能的样点值,如表1所示。
表1 成形滤波器的样点值
- 周立功:如何兼顾学习ARM与FPGA(05-23)
- 初学者如何学习FPGA(08-06)
- 为何、如何学习FPGA(05-23)
- FPGA 重复配置和测试的实现(08-14)
- 适用于消费性市场的nano FPGA技术(09-27)
- 赛灵思“授之以渔”理论:危机中如何巧降成本(06-04)
