充分发挥FPGA浮点IP内核的优势
时间:10-13
来源:互联网
点击:
对于通信、军事、医疗等应用中的很多复杂系统,首先要使用浮点数据处理算法,利用 C或者 MATLAB软件进行仿真和建模。而最终实现几乎都采用定点或者整数算法。算法被仔细映射到有限动态范围内,调整数据通路中的每一功能。这就需要很多取整和饱和步骤,如果处理的不合适,就会对算法性能有不利的影响。在集成过程中一般还需要进行大量的验证工作,以确保系统工作符合仿真结果。
以前,由于缺乏 FPGA工具包的支持, FPGA设计人员一般不选择浮点算法。使用很多浮点 FPGA运算符时,由于需要大量逻辑和布线资源,因此,它的另一个缺点是性能太差。 FPGA高效实现复数浮点函数的关键是使用基于乘法器的算法,利用大量集成在 FPGA器件中的硬件乘法器资源。用于实现这些非线性函数的乘法器必须有很高的精度,以保证乘法迭代过程中的精度要求。而且,高精度乘法器不需要在每一次乘法迭代中进行归一化和逆归一化处理,大大降低了对逻辑和布线的要求。
FPGA采用硬件数字信号处理 (DSP)模块,能够实现高效的 36位x36位乘法器,对于单精度浮点算法,提供足够的位数,满足一般的单精度 24位尾数要求。这些乘法器还能够用于构建更大的乘法器,实现高达 72位 x72位的双精度浮点算法。
由于浮点算法动态范围较大,相对于浮点仿真,大大简化了系统性能验证任务,因此,对于设计人员而言,这种算法通常能够提高性能。在某些应用中,定点算法是不可行的。动态范围要求使用浮点算法的一个常见的例子是矩阵求逆运算。
浮点 IP内核
Altera现在提供业界最全面的单精度和双精度浮点 IP内核,其性能非常高。目前提供的浮点 IP内核包括:
基本功能
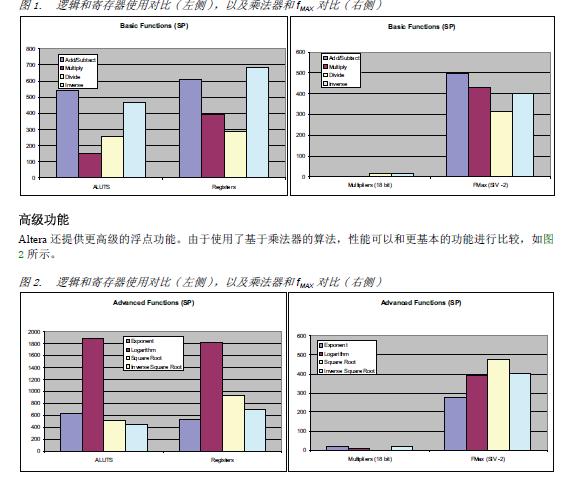
图1详细列出了基本浮点功能及其性能。对比浮点除法与加减法所需要的资源及其性能,表明系统设计人员不需要在算法中避开除法运算以简化硬件实现。
矩阵乘法
Altera在提供基于 FPGA的参数赋值浮点矩阵IP内核方面有其独到之处。这些运算符集成了数十甚至上百个浮点运算符,保持了较高的性能。矩阵乘法内核还可以用于完成标准测试或者 GFLOP/S和 GFLOP/W。
SGEMM矩阵乘法内核的性能结果如表1所示,它实际是后编译时序逼近结果,与确定 GFLOP/S通常使用的 Altera公司充分发挥 FPGA浮点 IP内核的优势 纸笔浮点计算方法不同。任何其他 FPGA供应商都不支持这类基准测试,用户使用 Altera Quartus. II软件中提供的参数赋值矩阵乘法 IP内核,很容易自己进行测试。
表 1. 单精度矩阵乘法性能结果

注释:
(1) 自适应逻辑模块
(2) 18x18 DSP模块
使用 Quartus II功耗估算器,很容易计算得到实际的每瓦每秒 giga浮点结果 (GFLOPS/W)。使用 Altera. Stratix. IV EP4SE230 FPGA部分资源时,结果达到了 5 GFLOPS/W。使用 Stratix IV EP4SE530器件中更大的矩阵乘法内核,结果大约为 7 GFLOPS/W,计算密度为 200 GFLOPS。利用整个器件实现大规模浮点算法时,分散了 FPGA静态功耗,效率非常高。
Altera开发的浮点技术大大降低了实现大规模浮点数据通路的逻辑和布线资源要求。使用浮点数据通路优化工具非常关键,对资源要求的降低使得单位浮点逻辑/布线运算比达到了高端 FPGA的水平。这反映在工具能够实现接近 300 MHz的 fMAX,与例化的矩阵乘法规模无关。通过这种方式,在大规模浮点设计中,用户能够可靠的使用 FPGA 80%以上的资源,实现大于 200-MHz的 fMAX性能。
矩阵求逆
FPGA中浮点算法最常见的应用是矩阵求逆。大部分无线多输入多输出 (MIMO)算法、雷达 STAP系统、医疗成像聚束和很多高性能计算应用都需要进行矩阵求逆。参数赋值矩阵求逆浮点 IP内核的实例性能 (表2)显示了非常高的矩阵吞吐量。 4x4矩阵求逆内核能够进行每秒 2千万次矩阵求逆运算,速度足以支持 LTE无线 MIMO应用。
表 2. 单精度浮点矩阵求逆 (Cholesky算法)性能
快速傅立叶变换
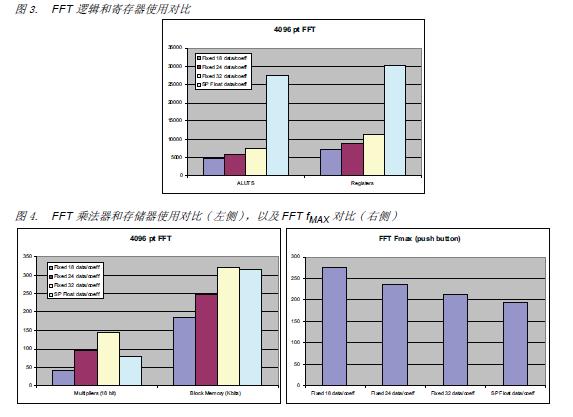
FFT是另一种大动态范围应用实例。由于 FFT算法的内在特性,位精度一般会随着 FFT长度增加而增大。某些应用使用级联 FFT,需要更大的动态范围。很多雷达应用使用 FFT进行定点算法,装入测距数据。这一般还需要第二次 FFT,装入多普勒测距数据,动态范围足够高,需要采用浮点算法。如图3和图4所示,相对于定点算法,需要增加逻辑以实现单精度浮点算法,而电路 fMAX、存储器和乘法器基本相似。
以前,由于缺乏 FPGA工具包的支持, FPGA设计人员一般不选择浮点算法。使用很多浮点 FPGA运算符时,由于需要大量逻辑和布线资源,因此,它的另一个缺点是性能太差。 FPGA高效实现复数浮点函数的关键是使用基于乘法器的算法,利用大量集成在 FPGA器件中的硬件乘法器资源。用于实现这些非线性函数的乘法器必须有很高的精度,以保证乘法迭代过程中的精度要求。而且,高精度乘法器不需要在每一次乘法迭代中进行归一化和逆归一化处理,大大降低了对逻辑和布线的要求。
FPGA采用硬件数字信号处理 (DSP)模块,能够实现高效的 36位x36位乘法器,对于单精度浮点算法,提供足够的位数,满足一般的单精度 24位尾数要求。这些乘法器还能够用于构建更大的乘法器,实现高达 72位 x72位的双精度浮点算法。
由于浮点算法动态范围较大,相对于浮点仿真,大大简化了系统性能验证任务,因此,对于设计人员而言,这种算法通常能够提高性能。在某些应用中,定点算法是不可行的。动态范围要求使用浮点算法的一个常见的例子是矩阵求逆运算。
浮点 IP内核
Altera现在提供业界最全面的单精度和双精度浮点 IP内核,其性能非常高。目前提供的浮点 IP内核包括:
- 加法 /减法
- 乘法
- 除法
- 倒数
- 指数
- 对数
- 平方根
- 逆平方根
- 矩阵乘法
- 矩阵求逆
- 快速傅立叶变换 (FFT)
- 对比
- 整数和分数转换
基本功能
图1详细列出了基本浮点功能及其性能。对比浮点除法与加减法所需要的资源及其性能,表明系统设计人员不需要在算法中避开除法运算以简化硬件实现。

矩阵乘法
Altera在提供基于 FPGA的参数赋值浮点矩阵IP内核方面有其独到之处。这些运算符集成了数十甚至上百个浮点运算符,保持了较高的性能。矩阵乘法内核还可以用于完成标准测试或者 GFLOP/S和 GFLOP/W。
SGEMM矩阵乘法内核的性能结果如表1所示,它实际是后编译时序逼近结果,与确定 GFLOP/S通常使用的 Altera公司充分发挥 FPGA浮点 IP内核的优势 纸笔浮点计算方法不同。任何其他 FPGA供应商都不支持这类基准测试,用户使用 Altera Quartus. II软件中提供的参数赋值矩阵乘法 IP内核,很容易自己进行测试。
表 1. 单精度矩阵乘法性能结果

注释:
(1) 自适应逻辑模块
(2) 18x18 DSP模块
使用 Quartus II功耗估算器,很容易计算得到实际的每瓦每秒 giga浮点结果 (GFLOPS/W)。使用 Altera. Stratix. IV EP4SE230 FPGA部分资源时,结果达到了 5 GFLOPS/W。使用 Stratix IV EP4SE530器件中更大的矩阵乘法内核,结果大约为 7 GFLOPS/W,计算密度为 200 GFLOPS。利用整个器件实现大规模浮点算法时,分散了 FPGA静态功耗,效率非常高。
Altera开发的浮点技术大大降低了实现大规模浮点数据通路的逻辑和布线资源要求。使用浮点数据通路优化工具非常关键,对资源要求的降低使得单位浮点逻辑/布线运算比达到了高端 FPGA的水平。这反映在工具能够实现接近 300 MHz的 fMAX,与例化的矩阵乘法规模无关。通过这种方式,在大规模浮点设计中,用户能够可靠的使用 FPGA 80%以上的资源,实现大于 200-MHz的 fMAX性能。
矩阵求逆
FPGA中浮点算法最常见的应用是矩阵求逆。大部分无线多输入多输出 (MIMO)算法、雷达 STAP系统、医疗成像聚束和很多高性能计算应用都需要进行矩阵求逆。参数赋值矩阵求逆浮点 IP内核的实例性能 (表2)显示了非常高的矩阵吞吐量。 4x4矩阵求逆内核能够进行每秒 2千万次矩阵求逆运算,速度足以支持 LTE无线 MIMO应用。
表 2. 单精度浮点矩阵求逆 (Cholesky算法)性能

快速傅立叶变换
FFT是另一种大动态范围应用实例。由于 FFT算法的内在特性,位精度一般会随着 FFT长度增加而增大。某些应用使用级联 FFT,需要更大的动态范围。很多雷达应用使用 FFT进行定点算法,装入测距数据。这一般还需要第二次 FFT,装入多普勒测距数据,动态范围足够高,需要采用浮点算法。如图3和图4所示,相对于定点算法,需要增加逻辑以实现单精度浮点算法,而电路 fMAX、存储器和乘法器基本相似。

仿真 FPGA DSP Altera Quartus LTE 电路 收发器 电子 相关文章:
- 基于FPGA的片上系统的无线保密通信终端(02-16)
- 基于ARM的嵌入式系统中从串配置FPGA的实现(06-09)
- 采用EEPROM对大容量FPGA芯片数据实现串行加载(03-18)
- 基于PLB总线的H.264整数变换量化软核的设计(03-20)
- FPGA按键模式的研究与设计(03-24)
- 验证FPGA设计:模拟,仿真,还是碰运气?(08-04)
