高速并行Reed-Solomon编解码器

1 引言

Reed-Solomon(简称RS)码是差错控制领域中一类重要的线性分组码，具有较强的纠正突发错误和随机错误的能力，广泛应用于各种差错控制领域。RS解码器可在FPGA或ASIC上实现IP核。但目前国内RS编码速度约为400 Mb／s，纠错能力为4 bit，仍存在编码速度低、纠错能力不完善、系统的吞吐率受限等问题。因此提出一种改进的IBM算法．进一步提高RS编码器的编码速度及纠错能力，扩大应用范围。这样RS编解码器能够实现远距离传输信息，太空航天通信的快速存储及全球定位系统需求。

2 RS编解码原理

2．1 编码原理

m=(m0，m1…mk-1)表示GF(28)的k位信息符号序列，该信息矢量多项式：m(x)=m+m1x+…+mk-lxk-1。将左移2t位的信息多项式与生成多项式g(x)相除，得到：p(x)=x2m(x)modg(x)，c(x)=x2tm(x)+p(x)。显然，以矢量表示编码后的码字为：C=(p，p，…p，m，m，…m)。编码的码字C中，信息位可以清晰地与校验位区分开。因此，RS编码的实质就是解决以生成多项式g(x)为模的除法问题。

2．2 解码原理

RS解码算法分时域解码算法和频域解码算法。这里主要讨论时域解码算法。时域解码是将码字看成时间轴上的信号序列，利用码的代数结构进行解码。常见的IBM算法解码分为四个步聚：①由接收的码字R(x)计算伴随式S(x)；②根据关键方程计算错误值多项式w(a)和错误位置多项式σ(x)；③钱搜索找到错误位置，并计算错误值；④纠正错误。图1为RS编解码系统原理图，其中虚线框部分是编码器流程。其余则为解码流程。

3 实现RS(204，188)编解码器

3．1 RS优化的编码方法

传统的编码器算法实现RS(204，188)编码器，需要16个有限域乘法器和16个有限域加法器。根据RS码型的确定来固定RS码的生成多项式，图2中g0,g1……g15为常数，RS编码器逻辑电路的乘法器则变为常数×变量的形式，利用有限域常数乘法器的特点，对编码器进行两级优化，具体操作如下：①)GF(28)域上的RS(204，188)生成多项式为：g(x)=(x+1)(x+a)(x+a2)…(x+a15)，其中a，a2…a15为GF(28)的本原元。生成多项式确定后，计算得到生成多项式的16个系数g0，g1…g15。当有限域乘法器的一个乘数为常数时，乘数运算时只需模2运算所需的异或门而不用与门；②预先计算出现频率较高的并或运算，使用新元素代替矩阵中重复出现的异或计算，这样就实现乘法器结构的第二级优化。



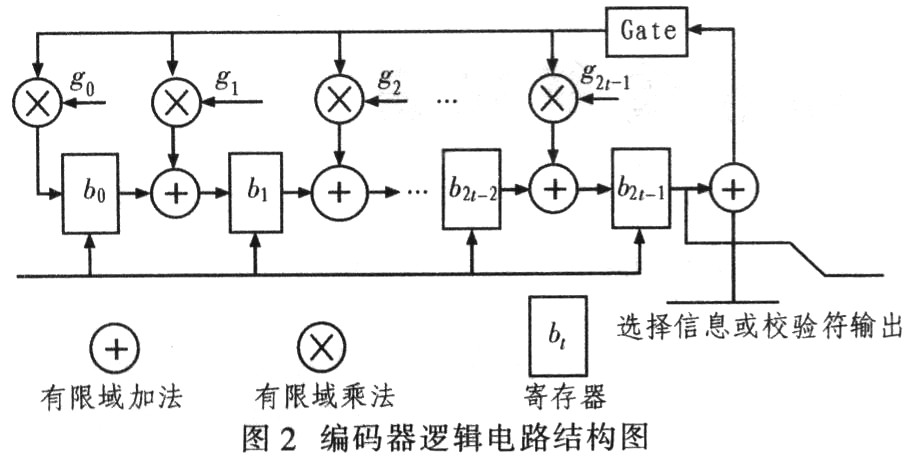
利用上述两种优化RS编码器的乘法器的方法能够实现RS(204，188)编码器，可节省RS(204，188)编码器资源20％。

3．2 解码实现电路

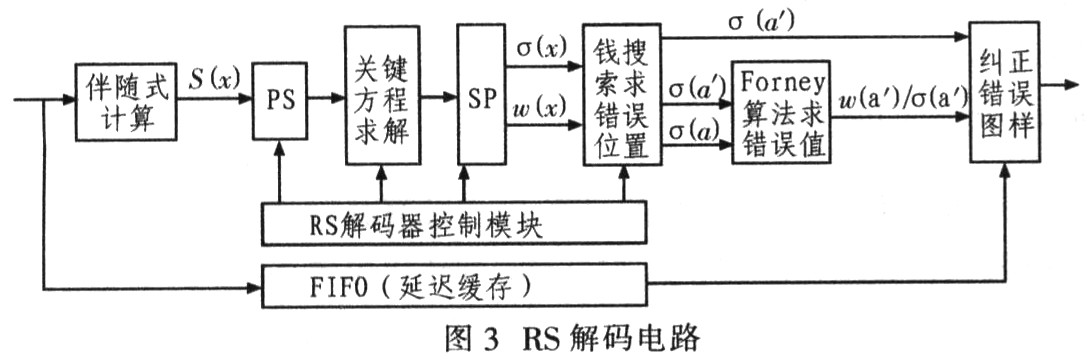
RS(204，188)编码解码器的解码按以下四个步骤实现：①从接收到的码字R(x)计算伴随式S(x)；②利用IBM算法计算错误位置多项式σ(x)和错误值多项式w(x)；③利用钱搜索算法找出错误位置；④利用Fomey算法计算错误值，与FIFO控制器所存储的接收码字相异或，得到正确的传输码字。图3给出RS(204，188)编解码器的解码电路。



3．3 改进的流水线结构

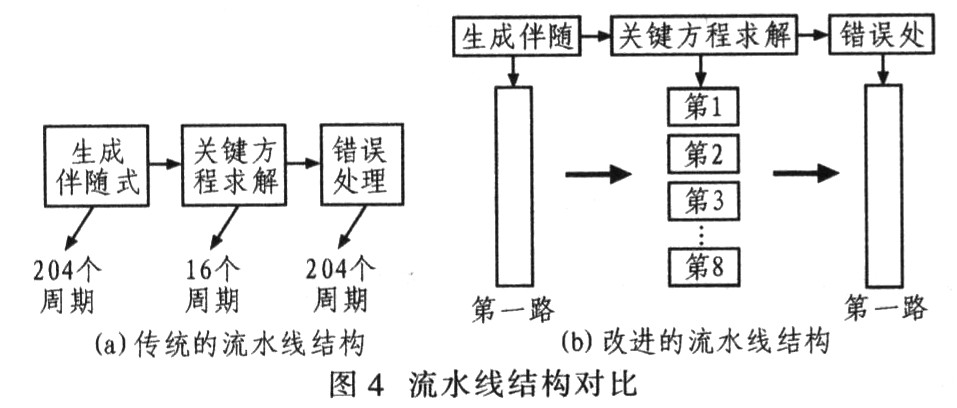
图4给出了传统和改进的流水线结构对比。传统的流水线结构各模块处理周期差距很大，约达8：1比例，造成周期极大浪费。改进的流水线结构则采用时分复用，可在相应的处理周期不变的情况下可将并行处理的数据率提高到原数据率的8倍。



4 FPGA仿真测试

在OuatusⅡ5．O平台上采用Verilog编写编解码器代码，测试步骤为：分析与综合；生成功能网表；配置输入信号波形；功能仿真；整体编译；时间仿真。

4．1 系统性能测试

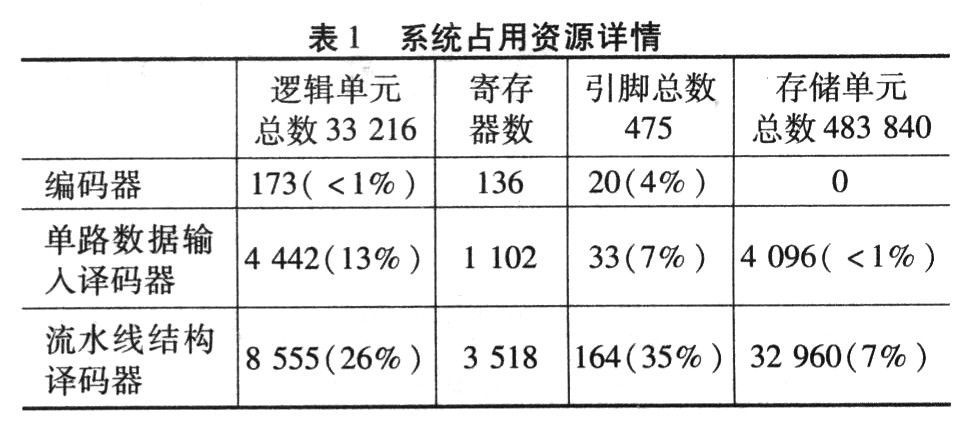
(1)资源利用率综合功能仿真和时间仿真的编译报告，系统占用资源详细情况如表1所示。



(2)解码数据率解码数据率=每帧数据的字节数×解码频率／系统所需周期。采用Ahera公司的RS解码器的IP器件，使用CycloneⅡ器件，其解码数据率为104 Mb／s。由该设计的时序仿真表明解码器8路复用后的解码数据率高达116．65 Mb／s。

(3)纠错能力及纠错仿真纠错能力由码型、解码算法、控制信号、时钟等因素共同决定，该设计的单路数据输入解码器最大纠错能力为7字节／204字节(每帧数据204字节，纠正随机错误7字节)，接近RS码的纠错上限8字节／204字节。8位输入数据发生错误：02H～09H变成了01H，经系统纠错得到正确的输出波形。

4．2 系统构造

(1)查表法代替复杂的求逆单元为了获得更高的解码速率，使用更少的FPGA资源，系统设计使用标准基到复数基的变换与逆变换，用复数基进行乘法器设计，除法器设计是把处理数据从标准基转化为指数幂的表示形式，改用高效查表法代替复杂的求逆单元，将σ(x)的逆单元按照寻址方式转换为表格形式，在程序中直接调用，简化设计，提高了解码频率。

(2)并行流水线结构 由于传统设计是利用SC模块求解伴随式，KES模块求解关键方程，CESS模块求解错误位置和错误值，它们之间的处理周期差距很大，造成周期的极大浪费。而采用时分复用的流水线结构可有效解决这一问题，对结构简单的模块进行复用，在处理周期基本不变的情况下，从而提高并行处理的解码数据率。