FCSR原理及其VHDL语言的实现
时间:08-02
来源:互联网
点击:
伪随机信号在雷达、遥控、遥测、通信加密和无线电测量系统领域有着广泛的应用,其产生方法有多种途径。进位反馈移位寄存器(feedbackwithcarryshiftregiste,FCSR)由Klapper和Goresky于1993年提出,是一类较新颖的方法,其理论实质类似于数学上产生随机数的模2同余法。经过一系列理论分析后普遍认为在序列密码的分析和设计中具有一定价值。
本文简要介绍了FCSR的基本原理和特性,重点讨论基于硬件描述语言VHDL的可变长FCSR的设计。VHDL可编程逻辑器件CPLD/FPGA结合使用,可以方便、灵活地实现此类伪随机序列发生器。
1 FCSR产生原理和序列特性
某时刻一个r级(非退化)FCSR如图1所示。其中ai∈GF(2), (i=n-1,n-2,…,n -r),mn-1∈Z,qi∈GF(2),(i=1,2,…,r-1),qr=1,∑为一般的整数加法。工作过程如下:
(1)计算整数和:
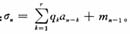
(2)移位寄存器右移一位,输出an-r。
(3) an=σn(mod 2)反馈入移位寄存器。
(4) mn=[σn/2]反馈入进位寄存器。
记q0= -1,FCSR的一个状态为(mn-1;an-1,…,

为FCSR的连接数。
FCSR能返回到自身的状态称为周期状态。以q为连接数的FCSR的周期状态个数为q+1,其中平凡的周期状态(0;0,…,0)和(w-1;1,…,1)在状态图中形成2个长为1的圈,非平凡周期状态的个数为q-1,其余状态都是非周期的。其中w=wt(q+1)为q+1的汉明重量,指qi(i=0,1,…,r)中qi≠0的个数。
以q为连接数的FCSR相应的有理数为p/q。其中,
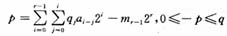
且q为奇数。如果p和q互素,那么a有周期T=ordq(2)。特殊的,如果T=Φ(q)(φ为欧拉函数),即2为模q的本原根,那么该序列达到他的最大周期。由欧拉函数的性质可知,此时Φ(q)=q-1。称其为连接数为q的最大周期FCSR序列,或l序列。
由于在FCSR中,初始状态、移位寄存器级数、抽头数目、抽头位置的变化都会产生不同的序列,因此可以通过设计参数可变的FCSR发生器来生成周期更长的伪随机序列。
2 FCSR序列发生器的VHDL实现
以n=10为例来设计参数可变的FCSR序列发生器。
2.1 功能描述及外部引脚
由图1可知,进位反馈移位寄存器由加法器、进位寄存器和一组(n级)D触发器组成。加法器实现FCSR的反馈运算;进位寄存器保存前一时刻运算结果除2后的状态mn-1,并为下一运算提供输入;n级D触发器构成移位寄存器,在时钟控制下实现右移,依次输出其内部状态。同时某些触发器的输出反馈回来,与进位寄存器的输出进行运算,和模2反馈至寄存器输入端,和除2反馈至进位寄存器。
式(1)中qi∈GF(2) ,(i=1,2,…,r-1)在实际电路中为抽头的连接状态,决定哪一级输出反馈至加法器,qi=0表示断开,qi=1表示连接。
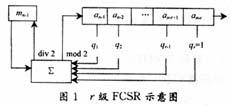
FCSR序列发生器的外部引脚定义如图2所示。
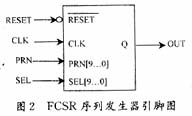
其中,CLK为时钟信号;RESET为置数信号;PRN为初态置数端;SEL为抽头置数端;Q为输出端。该FCSR序列发生器的特点在于可以通过设定SEL[9…0]的值来改变抽头数、抽头位置和发生器的有效级数n(1"10级);当RESET为低电平时,通过设定PR N[9…0]的值改变FCSR的初态,从而可以改变输出序列周期,分析各种状态下输出 序列的变化。
2.2 可变参数部分的设计
本设计通过手动或软件自动设定SEL[9…0]的值来改变抽头数、抽头位置和发生器的有效级数3个参数,其中改变最高抽头位置可使有效长度可变。具体电路中,由SEL[9…0]设定值作为加法器的输入,输出结果进行下一步运算,因此需要设计输入变量较多、延迟时间较短的加法器电路。
这里的求和运算可以等效为计算输入变量中“1”的个数。对此有多种实现方案,如计数法、逻辑函数法、查表法、求和网络法等。单纯使用一种方法,在输入变量较多的情况下会有占用资源太多、延迟时间太大或表达式太繁琐等问题,因此需要综合使用这些方法。该加法器综合使用逻辑函数-求和网络法,由1位累加器和3位串行加法器实现。
由于n=10,则抽头数至多为10,可以分2组进行求和。因此首先设计5输入、3位输出的累加器。用卡诺图简化后,写逻辑表达式如下:
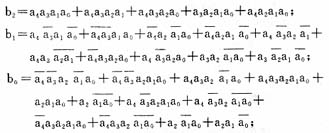
3位串行加法器的设计比较简单,不再赘述,则10输入变量、3位输出的加法器电路原理图如图3所示。
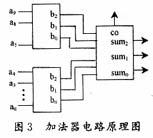
这里求和网络只有1级,不难由此扩充成多级。该电路延迟至多为8级逻辑门的延迟时间,占用资源也较少。
2.3 主程序
根据FCSR序列产生的原理,采用VHDL语言的混合描述方式对该逻辑进行硬件描述。主程序l_seq如下:


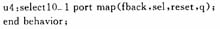
其中元件例化语句中所引用的元件已经作为组件在components.vhd用户包进行定义,在主程序中调用即可。
本文简要介绍了FCSR的基本原理和特性,重点讨论基于硬件描述语言VHDL的可变长FCSR的设计。VHDL可编程逻辑器件CPLD/FPGA结合使用,可以方便、灵活地实现此类伪随机序列发生器。
1 FCSR产生原理和序列特性
某时刻一个r级(非退化)FCSR如图1所示。其中ai∈GF(2), (i=n-1,n-2,…,n -r),mn-1∈Z,qi∈GF(2),(i=1,2,…,r-1),qr=1,∑为一般的整数加法。工作过程如下:
(1)计算整数和:
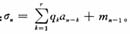
(2)移位寄存器右移一位,输出an-r。
(3) an=σn(mod 2)反馈入移位寄存器。
(4) mn=[σn/2]反馈入进位寄存器。
记q0= -1,FCSR的一个状态为(mn-1;an-1,…,

为FCSR的连接数。
FCSR能返回到自身的状态称为周期状态。以q为连接数的FCSR的周期状态个数为q+1,其中平凡的周期状态(0;0,…,0)和(w-1;1,…,1)在状态图中形成2个长为1的圈,非平凡周期状态的个数为q-1,其余状态都是非周期的。其中w=wt(q+1)为q+1的汉明重量,指qi(i=0,1,…,r)中qi≠0的个数。

以q为连接数的FCSR相应的有理数为p/q。其中,
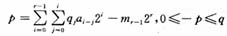
且q为奇数。如果p和q互素,那么a有周期T=ordq(2)。特殊的,如果T=Φ(q)(φ为欧拉函数),即2为模q的本原根,那么该序列达到他的最大周期。由欧拉函数的性质可知,此时Φ(q)=q-1。称其为连接数为q的最大周期FCSR序列,或l序列。
由于在FCSR中,初始状态、移位寄存器级数、抽头数目、抽头位置的变化都会产生不同的序列,因此可以通过设计参数可变的FCSR发生器来生成周期更长的伪随机序列。
2 FCSR序列发生器的VHDL实现
以n=10为例来设计参数可变的FCSR序列发生器。
2.1 功能描述及外部引脚
由图1可知,进位反馈移位寄存器由加法器、进位寄存器和一组(n级)D触发器组成。加法器实现FCSR的反馈运算;进位寄存器保存前一时刻运算结果除2后的状态mn-1,并为下一运算提供输入;n级D触发器构成移位寄存器,在时钟控制下实现右移,依次输出其内部状态。同时某些触发器的输出反馈回来,与进位寄存器的输出进行运算,和模2反馈至寄存器输入端,和除2反馈至进位寄存器。
式(1)中qi∈GF(2) ,(i=1,2,…,r-1)在实际电路中为抽头的连接状态,决定哪一级输出反馈至加法器,qi=0表示断开,qi=1表示连接。
FCSR序列发生器的外部引脚定义如图2所示。

其中,CLK为时钟信号;RESET为置数信号;PRN为初态置数端;SEL为抽头置数端;Q为输出端。该FCSR序列发生器的特点在于可以通过设定SEL[9…0]的值来改变抽头数、抽头位置和发生器的有效级数n(1"10级);当RESET为低电平时,通过设定PR N[9…0]的值改变FCSR的初态,从而可以改变输出序列周期,分析各种状态下输出 序列的变化。
2.2 可变参数部分的设计
本设计通过手动或软件自动设定SEL[9…0]的值来改变抽头数、抽头位置和发生器的有效级数3个参数,其中改变最高抽头位置可使有效长度可变。具体电路中,由SEL[9…0]设定值作为加法器的输入,输出结果进行下一步运算,因此需要设计输入变量较多、延迟时间较短的加法器电路。
这里的求和运算可以等效为计算输入变量中“1”的个数。对此有多种实现方案,如计数法、逻辑函数法、查表法、求和网络法等。单纯使用一种方法,在输入变量较多的情况下会有占用资源太多、延迟时间太大或表达式太繁琐等问题,因此需要综合使用这些方法。该加法器综合使用逻辑函数-求和网络法,由1位累加器和3位串行加法器实现。
由于n=10,则抽头数至多为10,可以分2组进行求和。因此首先设计5输入、3位输出的累加器。用卡诺图简化后,写逻辑表达式如下:
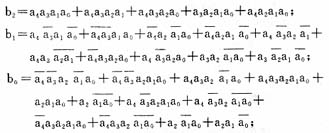
3位串行加法器的设计比较简单,不再赘述,则10输入变量、3位输出的加法器电路原理图如图3所示。

这里求和网络只有1级,不难由此扩充成多级。该电路延迟至多为8级逻辑门的延迟时间,占用资源也较少。
2.3 主程序
根据FCSR序列产生的原理,采用VHDL语言的混合描述方式对该逻辑进行硬件描述。主程序l_seq如下:


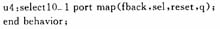
其中元件例化语句中所引用的元件已经作为组件在components.vhd用户包进行定义,在主程序中调用即可。
无线电 CSR VHDL CPLD FPGA 电路 仿真 相关文章:
- 基于Virtex-5 FPGA设计Gbps无线通信基站(05-12)
- 赛灵思详解新近推出的FPGA领域设计平台(12-16)
- 选择合适的FPGA千兆位收发器至关重要(10-28)
- Virtex-5推动超宽带通信和测距的发展(01-06)
- QPSK调制器的FPGA实现(03-22)
- 基于CPLD与单片机的高速数据采集系统(04-08)
