汽车变截面板簧轧机计算机控制系统的研究

介绍两辊式汽车变截面板簧轧机计算机控制系统的主要硬件结构､设计方法,以及多模态智能控制算法在液压伺服系统中的应用｡该控制系统设计合理,运行稳定,控制精度高｡

变截面轧机是生产汽车变截面板簧的关键设备｡它将加热到950℃的等截面弹簧钢板通过转动的轧辊压缩及拉拔机构拉拔,使其横断面按照设计的变形曲线改变｡目前国内钢板弹簧生产企业或者采用进口轧机如英国西尔公司､德国波克公司的某些产品,或者采用国产的仿西尔公司的三辊轧机及一些简易轧机｡简易轧机生产的产品精度低､展宽大,国产三辊轧机能耗､设备的体积较大｡

两辊式变截面轧机是目前国内开发出的技术含量较高的轧机产品｡该轧机机械液压结构设计紧凑,能耗低,机械结构中无侧辊限制板簧在轧制过程中的宽展,通过计算机控制轧制中的压下量和拉力及轧辊磨擦力的平衡及压下拉拔装置的位置伺服控制,保证轧制后板簧的展宽在1%以内｡

本文介绍两辊式轧机的计算机控制系统设计｡该轧机由液压伺服系统驱动,采用IBM-PC工业控制计算机及可编程控制器控制｡

1 轧机结构及主要技术指标

1.1 轧机结构

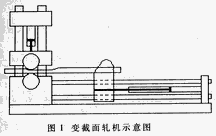
图1为两辊式变截面轧机示意图｡轧机的机械结构由一个钢制构架支撑和轧辊驱动机构及拉拔机构组成,轧辊由液压马达驱动,上轧辊由伺服油缸控制上下运动,拉拔机构由导柱和液压夹紧装置构成,由水平伺服油缸控制做水平方向运动｡由液压蓄能器稳定压下的压力,液压马达输出的扭矩由一比例减压阀控制｡由两个旋转编码器检测X､Y方向的位移和速度｡



1.2 轧机的主要性能指标

• 最大轧制长度:1200mm

• 最小轧制长度:300mm

• 板坯最大厚度:50mm

• 板坯最大宽度:160mm

• 最大轧制力:760kN

• 最大拉拔力:200kN

• 最大轧制速度:30m/min

• 产品厚度公差:±0.1mm

• 产品宽度公差:板宽≤100mm ±1mm,板宽>100mm ±1%

2 计算机控制系统设计

2.1 总体设计

  轧机控制系统的被控量可分为模拟量部分和开关量部分｡模拟量部分由四路组成,分别控制液压系统的输出流量､液压马达的输出扭矩､拉拔油缸运动速度､压下油缸的运动速度｡模拟量部分由一台IBM-PC 486DX2-66工控机控制｡开关量部分由一台MASTERK200可编程控制器(PLC)控制,这些控制包括液压站的油温控制､轧辊的冷却､操作按钮站､拉拔方向的制动限位､轧辊及液压系统的润滑控制､轧机的状态检测及故障报警､各相关部分间的互锁控制等｡工控机与PLC间通过开关量接口进行通讯｡这样即减轻IBM-PC的运算量,缩短了控制周期;避免控制集中造成的控制风险集中,提高了系统的可靠性｡无论IBM-PC或PLC那一部分出现异常,系统均能采取必要的保护措施｡

2.2 控制系统硬件结构

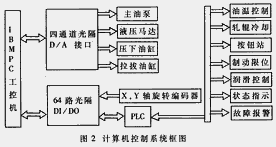
轧机的计算机控制系统结构如图2所示,由计算机､四路12位光隔D/A接口､64路光隔开关量输入输出接口(DI/DO)､可编程控制器(PLC)组成｡计算机通过DI/DO接口及RS232接口与PLC进行通讯｡采用两个12位绝对式光电编码器检测X､Y方向的位置和速度｡油温控制部分的作用是控制液压站的油温在允许范围内;轧辊冷却部分控制轧辊的冷却;按扭站用来输入控制命令;制动限位部分在轧机的拉拔机构超过停车范围时自动停车;润滑控制部分根据拉拔机构的运行次数控制润滑油缸自动向各润滑点加注润滑油;状态指示部分显示轧机的运行状态;故障报警部分在轧机出现异常时进行声光报警｡

2.3 多变量处理

在轧制过程中除了对拉拔､压下机构进行位置伺服控制外,还要保证液压系统的流量及液压马达的输出扭矩保持恒定｡轧机的控制系统为一多变量控制系统｡

  液压系统采用的伺服阀内部具有阀芯位置的闭环控制环节,可看作一比例环节｡为了简化控制器结构,根据设计要求,拉拔机构､液压系统的流量､液压马达的输出扭矩分别采用开环控制,系统近似为单变量系统｡由于产品的截面变形曲线的斜率较小,即压下装置的运动速度远小于拉拔机构的运动速度｡所以即使拉拔方向采取开环控制,也可获得期望的控制效果｡

2.4 控制算法

采用智能控制算法对电液伺服系统已有成功的报道[1],对轧机这类具有双坐标的电液伺服系统,也选择了多模态仿人智能控制算法｡轧机的液压伺服系统具有大流量､高压力且拉拔方向运动的最高速度为30m/min,控制对象有一定的非线性､时变性｡在设计有效的控制算法时,首先应考虑控制系统的实时性,这要求控制系统的结构不应该很复杂的,其决策和推理应是快速的｡



多模态控制就是在控制过程中根据系统不同的特征状态,控制器采用不同的控制策略和控制模式的一种控制算法｡特征状态是指一些反映系统特性､特征变化以及所处状态的特征量的集合,用Gi表示｡所有的特征状态构成一个特征状态集,用G表示｡则有

G=<G1,G2,…,Gm>

其中 Gi=(Gi1,Gi2,…,Gih) (i=1,2,…,m)

控制模式用Ai表示,所有的控制模式构成了多模态控制器的控制模式集,用A表示｡

A=<A1,A2, …,Am>

其中 Ai=U=f(Gij) (i=1,2,…,m;j=1,2,…,h)

  控制的实现就是由G到A推理过程的实现｡可由产生式规则IF G THEN A来表达｡

(1) G1:(|E|≤b1)∩(||≤b2)

A1:(U(n)=U(n1))

(2) G2:(EE≥0)∩[(|E|>b)1∪(|E|>b2)) ?

A2:U(n)=U0+Kp(E+KdTdE+Ei / TiEiT

(3) G3:(EE<0)∩[(|E|>b1)∪(|E|>b2)]

A3:U(n)=U0+KKp(Em(1)+EI+KdTdE)

为了获得良好的实时性,同时也考虑控制精度的要求,应尽可能选择较少的特征状态｡考虑控制系统的稳定性,选取误差及其一阶导数为基本特征量,经过这样的处理及大量的人-机在线学习的基础上,总结出下列三种基本的特征状态和相应的控制模式｡

其中U(n)为控制量的第n次输出值;U0为控制量在误差过零时的保持值;b1,b2为常数;Kp和K分别为比例增益及抑制系数;Kd,Ki,Td,Ti分别为微分和积分抑制系数及时间常数;T为采样间隔;Em(1)为第一次误差峰值;EI为G2状态下的区间积分值｡

文献[3]给出了控制对象的模型及仿人智能控制算法的仿真实验结果及与PID算法控制效果比较,从实验结果分析采用智能控制算法解决液压伺服系统的实时控制问题,能取得比PID控制算法更好的控制效果;控制器的设计不依赖对象的数学模型,对液压系统参数变化不敏感,鲁棒性强;算法简单,控制系统实时性好｡