Xilinx 20nm UltraScale架构助推无线电应用发展
时间:07-09
来源:互联网
点击:
UltraScale DSP48 Slice架构的优势
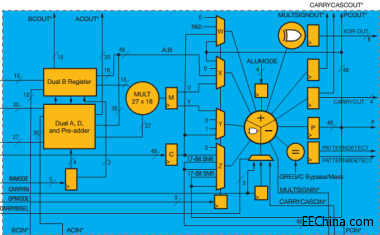
图1给出了UltraScale DSP48Slice(DSP48E2)的视图。上面的原理图(图表“a”)显示了详细架构,下面的原理图(“b”)强调了与7 系列Slice(DSP48E1)相比增强的功能。
*这些信号是专用于DSP48E2列的内部布线路径,其不可通过通用布线资源进行访问。
(a)详细的DSP48E2架构
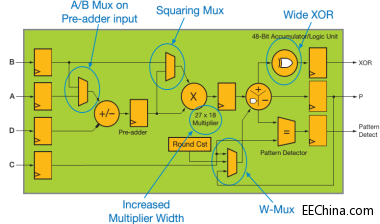
预加法器输入端上的A/B多路复用器
方形多路复用器
宽XOR
增加的乘法器宽度
W-多路复用器
(b)DSP48E2高层次功能视图
图1 – UltraScale DSP48 Slice架构
赛灵思用户指南UG579全面介绍了DSP48E2功能[7]。UltraScale架构的主要增强功能为:
46位输出端的45个最高有效位(MSBs)的计算方式为:
Z[45:1]=X[27:1]*Y[17:0]+X[0]*Y[17:1]
X的27个最高有效位和Y的18位可直接馈送到DSP48E2乘法器输入端,而X[0]*Y[17:1]源自外部17位AND运算符,并在一个流水线步骤后被发送到输入端C以匹配DSP48E2延迟。事实上AND运算符可通过由X[0]控制的复位引脚将Y[17:1]直接馈送到寄存器中。同样,外部1位AND运算符和用于实现延迟平衡的三时钟周期延迟可用来计算Z,Z[0]的LSB。
因此您可以执行具有单个DSP48E2 Slice和18个LUT/触发器对的28×18位乘法器。这同样适用于使用其它27个LUT/触发器对的27×19位乘法器。这两种情况下,均可通过W-mux支持运算结果的收敛舍入。
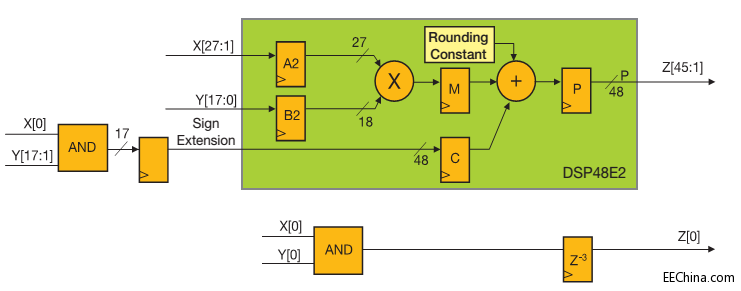
图2 – 具备输出收敛舍入功能的28×18位符号乘法运算
双精度浮点乘法运算涉及两个运算符的53位非符号尾数的整数乘积。尽管双精度浮点计数法中储存有一个52位数值(m),但它代表的是非符号尾数的小数部分,而实际上其是标准化的1+m值,需要将这些值乘在一起;因此乘法运算将要求使用附加位。考虑到两个53位操作数的MSB都等于1,并适当分解乘法运算从而以最佳方式利用DSP48E2 26×27位非符号乘法器及其改善后的各项功能(例如,由W-mux启动的真正的三输入48位加法器),可以看到,只需6个DSP48E2 Slice和极少的外部逻辑就可以构建53×53位非符号乘法运算。本文未涉及这类实现方式的所有细节,但在上一代7 系列器件上,要实现类似的方法则需要10个DSP48E1 Slice;因此UltraScale架构将需要的Slice数量减少了40%。
DSP48E2的27×18乘法器对于以融合数据路径为基础的应用非常实用。最近,IEEE浮点标准中加入了融合乘累加运算符概念[8]。一般来说,这包括建立浮点运算A*B+C,且乘法器和加法器之间无需明确舍入、标准化和非规范化的数据。当使用传统的浮点运算时,这些功能的代价非常高昂,且占用了最多的延迟时间。可推广这一概念以建立积和运算符,这在线性代数中非常常见(矩阵积,Cholesky分解法)。因此,这种方法在成本或时间紧迫的情况下十分高效,同时要求具备浮点计数法的准确性和动态范围。在无线电DFE应用中,数字预失真功能通常要求一些硬件加速来支持,以提高非线性滤波器系数的更新速度。然后,您可以在FPGA架构中建立一个或多个浮点MAC引擎,以协助软件中运行的系数估算算法(例如,在Zynq SoC的一个ARM®CortexTM-A9核上)。
对于这类算术结构,已经证明如果尾数宽度略有上升,从23位上升到26位,则与真正的单精度浮点实现相比,准确度会有所提高,但会减少延迟和空间占用。UltraScale架构非常适合该用途,因为它只需2个DSP48 Slice就可以打造单精度的融合乘法器,而7 系列器件则需使用3个Slice以及其它架构逻辑。
预加法器集成在位于乘法器前面的DSP48 Slice中,可提供一种高效的对称滤波器实现方式,这在DFE设计中很常见,可以实现数字上变频器(DUC)和数字下变频器(DDC)功能。对于N抽头对称滤波器来说,其输出实例的计算方式如下:
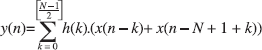
其中x(n)代表输入信号,h(n)代表滤波器脉冲响应,其中h(n)=h(N-1-n)。
因此,成对的输入实例会被馈送入预加法器中,而输出则会进一步乘以相应的滤波器系数。在7 系列架构上,预加法器必须使用DSP48E1的30位输入端(A)以及25位输入端(D),且其输出端需连接乘法器的25位输入端,同时将输入端B布线至18位乘法器输入端。
通过额外的W-mux多路复用器可将第四个输入操作数添加到ALU中对无线电应用最为有益。
因此,在建立对称滤波器时,系数数值化后不得超过18位,这样可将阻带衰减限制在85到90dB左右。对于新一代5G无线电系统来说,这也许会成为问题,因为该系统很可能在干扰水平较高的环境下运行,因此也许需要更大的衰减。
UltraScale架构解决了这个问题,因为可选择预加法器输入端作为A或B,并在输出端集成了一些多路复用逻辑,从而支持将D±A或D±B馈送至任意乘法器输入端(27位或18位输入端)。因此,可支持系数达27位的对称滤波器。赛灵思还为DSP48E2 Slice添加了另一项功能,将预加法器输出端连接至乘法器的两个输入端(在18位输入端上设有恰当的MSB截断)。这样便可以执行多达18位数据的(D±A)²或(D±A)²运算,从而可有效用于评估平方误差项的总和。此类运算在优化问题中十分常见,比如,在实施最小平方解决方案以获得调制解调器均衡器系数时,或按时间排列两个信号时。
毫无争议,通过额外的W-mux多路复用器将第四个输入操作数添加到ALU中对无线电应用最为有益。相比7 系列器件上针对此类设计相同的实现方案,这个操作数通常可以将DSP48需求量减少10%-20%。
只能将W-mux输出加入ALU(不允许减少)中,并可将其动态设置为寄存器C或P内容,或在FPGA配置过程中将其设为常量值(比如用于DSP48输出端的收敛舍入或对称舍入的常量),或只需将其归零。通过这种方式可在使用乘法器时执行真正的三输入运算,如A*B+C+P,A*B+C+PCIN,A*B+P+PCIN,而这在7 系列架构中是不可能实现的。的确,使用乘法器阶段会生成最后两个部分乘积输出,然后将其添加到ALU中,以完成运算(见图1)。因此,启动乘法器后,乘法器将使用ALU的两个输入端并执行一项三输入运算,而7 系列器件则无法执行。
受益于这一额外ALU输入端的两个最主要实例是半并行滤波器和复合乘积累加(MAC)操作数。下面我们将对这两个实例进行详细讲解。
图1给出了UltraScale DSP48Slice(DSP48E2)的视图。上面的原理图(图表“a”)显示了详细架构,下面的原理图(“b”)强调了与7 系列Slice(DSP48E1)相比增强的功能。

*这些信号是专用于DSP48E2列的内部布线路径,其不可通过通用布线资源进行访问。
(a)详细的DSP48E2架构

预加法器输入端上的A/B多路复用器
方形多路复用器
宽XOR
增加的乘法器宽度
W-多路复用器
(b)DSP48E2高层次功能视图
图1 – UltraScale DSP48 Slice架构
赛灵思用户指南UG579全面介绍了DSP48E2功能[7]。UltraScale架构的主要增强功能为:
- 赛灵思将乘法器的宽度从25×18增加到27×18,预加法器宽度也相应增加到27位。
- 您可以选择预加法器输入端为A或B,输出端集成了一些多路复用器逻辑,从而允许在任意乘法器输入端上(27位或18位输入)馈送D±A或D±B。
- 预加法器输出端可馈送两个乘法器输入(在18位输入端上有适当的MSB截断),因此允许计算高达18位数据的(D±A)²或(D±B)²。
- 通过额外的W-mux多路复用器在算术逻辑单元(ALU)中添加了第四个操作数,可将其看作输入端C、P或一个常量值(在FPGA配置时定义)。这样,使用乘法器时便可以执行一个三输入操作,如A*B+C+P或A*B+P+PCIN。值得注意的是,只能在ALU中添加W-mux输出(不允许减少)。
- 赛灵思集成了其它逻辑,从而可在X、Y或Z多路复用器输出端中的任意两个之间执行96位宽异或。实际上此处可提供四个不同模式,1x96位、2x48位、4x24位或8x12位异或操作。
46位输出端的45个最高有效位(MSBs)的计算方式为:
Z[45:1]=X[27:1]*Y[17:0]+X[0]*Y[17:1]
X的27个最高有效位和Y的18位可直接馈送到DSP48E2乘法器输入端,而X[0]*Y[17:1]源自外部17位AND运算符,并在一个流水线步骤后被发送到输入端C以匹配DSP48E2延迟。事实上AND运算符可通过由X[0]控制的复位引脚将Y[17:1]直接馈送到寄存器中。同样,外部1位AND运算符和用于实现延迟平衡的三时钟周期延迟可用来计算Z,Z[0]的LSB。
因此您可以执行具有单个DSP48E2 Slice和18个LUT/触发器对的28×18位乘法器。这同样适用于使用其它27个LUT/触发器对的27×19位乘法器。这两种情况下,均可通过W-mux支持运算结果的收敛舍入。

图2 – 具备输出收敛舍入功能的28×18位符号乘法运算
双精度浮点乘法运算涉及两个运算符的53位非符号尾数的整数乘积。尽管双精度浮点计数法中储存有一个52位数值(m),但它代表的是非符号尾数的小数部分,而实际上其是标准化的1+m值,需要将这些值乘在一起;因此乘法运算将要求使用附加位。考虑到两个53位操作数的MSB都等于1,并适当分解乘法运算从而以最佳方式利用DSP48E2 26×27位非符号乘法器及其改善后的各项功能(例如,由W-mux启动的真正的三输入48位加法器),可以看到,只需6个DSP48E2 Slice和极少的外部逻辑就可以构建53×53位非符号乘法运算。本文未涉及这类实现方式的所有细节,但在上一代7 系列器件上,要实现类似的方法则需要10个DSP48E1 Slice;因此UltraScale架构将需要的Slice数量减少了40%。
DSP48E2的27×18乘法器对于以融合数据路径为基础的应用非常实用。最近,IEEE浮点标准中加入了融合乘累加运算符概念[8]。一般来说,这包括建立浮点运算A*B+C,且乘法器和加法器之间无需明确舍入、标准化和非规范化的数据。当使用传统的浮点运算时,这些功能的代价非常高昂,且占用了最多的延迟时间。可推广这一概念以建立积和运算符,这在线性代数中非常常见(矩阵积,Cholesky分解法)。因此,这种方法在成本或时间紧迫的情况下十分高效,同时要求具备浮点计数法的准确性和动态范围。在无线电DFE应用中,数字预失真功能通常要求一些硬件加速来支持,以提高非线性滤波器系数的更新速度。然后,您可以在FPGA架构中建立一个或多个浮点MAC引擎,以协助软件中运行的系数估算算法(例如,在Zynq SoC的一个ARM®CortexTM-A9核上)。
对于这类算术结构,已经证明如果尾数宽度略有上升,从23位上升到26位,则与真正的单精度浮点实现相比,准确度会有所提高,但会减少延迟和空间占用。UltraScale架构非常适合该用途,因为它只需2个DSP48 Slice就可以打造单精度的融合乘法器,而7 系列器件则需使用3个Slice以及其它架构逻辑。
预加法器集成在位于乘法器前面的DSP48 Slice中,可提供一种高效的对称滤波器实现方式,这在DFE设计中很常见,可以实现数字上变频器(DUC)和数字下变频器(DDC)功能。对于N抽头对称滤波器来说,其输出实例的计算方式如下:
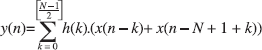
其中x(n)代表输入信号,h(n)代表滤波器脉冲响应,其中h(n)=h(N-1-n)。
因此,成对的输入实例会被馈送入预加法器中,而输出则会进一步乘以相应的滤波器系数。在7 系列架构上,预加法器必须使用DSP48E1的30位输入端(A)以及25位输入端(D),且其输出端需连接乘法器的25位输入端,同时将输入端B布线至18位乘法器输入端。
通过额外的W-mux多路复用器可将第四个输入操作数添加到ALU中对无线电应用最为有益。
因此,在建立对称滤波器时,系数数值化后不得超过18位,这样可将阻带衰减限制在85到90dB左右。对于新一代5G无线电系统来说,这也许会成为问题,因为该系统很可能在干扰水平较高的环境下运行,因此也许需要更大的衰减。
UltraScale架构解决了这个问题,因为可选择预加法器输入端作为A或B,并在输出端集成了一些多路复用逻辑,从而支持将D±A或D±B馈送至任意乘法器输入端(27位或18位输入端)。因此,可支持系数达27位的对称滤波器。赛灵思还为DSP48E2 Slice添加了另一项功能,将预加法器输出端连接至乘法器的两个输入端(在18位输入端上设有恰当的MSB截断)。这样便可以执行多达18位数据的(D±A)²或(D±A)²运算,从而可有效用于评估平方误差项的总和。此类运算在优化问题中十分常见,比如,在实施最小平方解决方案以获得调制解调器均衡器系数时,或按时间排列两个信号时。
毫无争议,通过额外的W-mux多路复用器将第四个输入操作数添加到ALU中对无线电应用最为有益。相比7 系列器件上针对此类设计相同的实现方案,这个操作数通常可以将DSP48需求量减少10%-20%。
只能将W-mux输出加入ALU(不允许减少)中,并可将其动态设置为寄存器C或P内容,或在FPGA配置过程中将其设为常量值(比如用于DSP48输出端的收敛舍入或对称舍入的常量),或只需将其归零。通过这种方式可在使用乘法器时执行真正的三输入运算,如A*B+C+P,A*B+C+PCIN,A*B+P+PCIN,而这在7 系列架构中是不可能实现的。的确,使用乘法器阶段会生成最后两个部分乘积输出,然后将其添加到ALU中,以完成运算(见图1)。因此,启动乘法器后,乘法器将使用ALU的两个输入端并执行一项三输入运算,而7 系列器件则无法执行。
受益于这一额外ALU输入端的两个最主要实例是半并行滤波器和复合乘积累加(MAC)操作数。下面我们将对这两个实例进行详细讲解。
赛灵思 无线电 DSP FPGA SoC DAC ADC 滤波器 ARM Cortex 相关文章:
- 赛灵思为以太网AVB网络流媒体传输推出高服务质量连接解决方案(01-12)
- 赛灵思扩大生态系统,重塑嵌入式视觉、工业物联网系统设计的未来(04-24)
- 基于赛灵思FPGA的数字频域干扰抵消器(11-23)
- 基于Virtex-5的串行传输系统设计与验证(12-24)
- 利用串行RapidIO交换机设计模块化无线基础系统(03-12)
- 一种可编程ExpressCard解决方案(07-15)
