基于赛灵思FPGA的数字频域干扰抵消器
时间:11-23
来源:互联网
点击:
作者:208研究所 田耘;北京邮电大学 徐文波 胡彬 谷涛 来源:电子产品世界 2009-11-10
项目背景
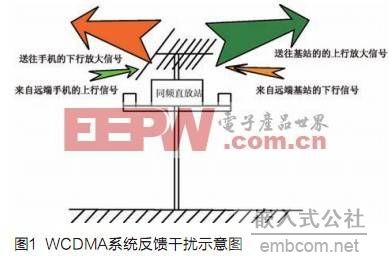
直放站在现代通信系统中是必不可少的,但是如果直放站的收发天线隔离度不够,整机增益偏大时,输出信号经延时后反馈到输入端,会使直放站输出信号发生严重失真产生自激。在无线通信系统的同频直放站中,为了减小产品体积以及缩短建站成本,收发天线常常放置在一起(或距离很近)。由于收发天线往往只存在方向角的不同,因此直放站的接收天线肯定会接收到其转发天线所发送的经过放大的信号,而对所期望接收的有用信号产生干扰。如果不对干扰信号进行处理,干扰和期望信号的叠加信号会再次被送进功放,再进行放大转发,干扰信号的强度会一直积累,最终使得直放站无法正常工作。这种正反馈式干扰(干扰信号与正常通信信号的调制参数和载波频率是完全一致的,使得接收机收到叠加有同频干扰的混合信号)还会对数字通信产生严重的电磁干扰,从而阻碍正常的通信。在上、下行链路中,往往都存在着这种反馈式干扰,如图1所示。
干扰抵消是同频直放站所必备的一项技术,也是信号处理领域一个非常重要的课题[1]。传统上,克服自激现象的方法有:(1)借助建筑物阻挡在发射和接收天线间; (2)增加直放站的施主和重发天线的空间隔离度。垂直隔离度一般最好大于1m,水平隔离度可以在十几米以上。如果没有垂直隔离的话,那么水平隔离的距离几乎达到200米;(3)降低直放站的增益:上行和下行按照比例,就是上下行链路平衡,直至消除自激。
虽然上述三种办法都可以在一定程度上降低干扰的影响,但是在某些场合,受到环境或系统性能的要求,这些方法并不可行。因此,利用自适应干扰抵消器来减少直放站设备的同频反馈干扰成为首选方案。在所有的自适应方案中,尤以频域算法在性能和复杂度之间取得良好平衡。
本项目以WCDMA系统为例,讨论数字频域自适应干扰抵消技术的实现,并从功率谱密度和星座图以及误差向量幅度(EVM)等性能指标对方案进行评价。在设计中,为了验证算法性能且保证接收端的正常工作,同时实现了WCDMA小区搜索的三步同步过程,并通过PC机对输入输出数据进行比对分析,验证方案性能。
系统方案
完整的系统从数字下变频后的基带数据开始,至数字上变频的前端为止,包括系统同步和干扰抵消两大组成模块,系统框图如图2所示,其简要介绍如下:
(1)在没有干扰的情况下,所采集的数据源从A点输入,然后将其构造为WCDMA信源,作为频域干扰抵消模块的输入。为了使干扰抵消模块正确运转,在本设计中的B点输出信号为每个码片4采样。
(2)为体现频域干扰抵消的作用,在系统中必须模拟一个干扰信号。本设计将D点的输出经过功放(PA)作为干扰信号。
(3)将干扰信号经过多径信道,反馈到B点与WCDMA信号叠加,再进入干扰抵消模块。为了抵消干扰,将E点的输出反馈到干扰抵消模块作为参考信号。在下文中,将此反馈支路称为辅链路;而干扰抵消+功放的链路称为主链路。
(4)有干扰的信号经过频域干扰抵消模块,输出抵消后的无干扰信号给同步模块,即D点。同步模块进行三步搜索,得到帧头以及扰码信息。对同步后的码片信号进行解扰解扩后得到信息数据,如图中G点输出。
(5)在开关1处,可以选择:有干扰的信号(C点)或者干扰抵消后的信号(D点)输入同步模块,并输出显示。
(6)在开关2处,可以选择:数据源直接显示(A点),或者是同步后解出的数据显示(G点)。
算法设计
频域自适应干扰抵消(AIC)模块利用了频域实现的LMS算法[2,3]。该算法通过1/2重叠保留法的快速傅立叶变换(FFT),在频域以直接相乘的计算方式实现快速相关和快速卷积[4]。算法基本框图如图3,其中A点为被干扰的信号,B为反馈链路的信号,C点为干扰被抵消后的输出。主要包括以下循环执行的操作流程,其中k表示第个k数据块:
(1)对自适应滤波器的M个频域抽头系数W(k)作初始化设置;
(2)将滤波器的时域连续输入信号u(n)每个M组成一个块,然后级联两个数据块做N点离散快速傅立叶变换,使其转换为频域信号U(k),并将此信号用作自适应滤波器的输入;其中N是该滤波器抽头个数M的2倍,即N=2M;
(3)将U(k)通过滤波器得到输出信号Y(k),然后进行快速傅立叶逆变换(IFFT)处理,使其转换为时域信号y(k),作为干扰的估计值;
(4)计算被干扰信号r(k)和y(k)的差值,即为干扰抵消后的信号d(k);再产生该期望信号的频域值D(k)为下一次滤波器抽头系数迭代所使用;
(5)利用频域信号进行最小均方误差LMS计算,即根据D(k)和U(k)对W(k)进行更新,并将此更新值返回到步骤(2)中使用。跳转到步骤(2)进行反复迭代,直至干扰被抵消。
与传统的时域LMS算法相比,利用频域LMS算法可以降低计算复杂度。假设输入为实信号,滤波器抽头个数为。可以得到,频域LMS和时域LMS的计算复杂度之比为
。实际中,干扰在空中传输的时延会比反馈信号的时延大得多,这时需要较大的抽头个数才能抵消干扰。假设M=1024,则频域LMS算法可以比时域LMS算法的速度提高大约16倍。为简化起见,在本文档中取M=64,利用频域LMS算法,在计算量角度大约可以比时域LMS算法快1.5倍。
项目背景
直放站在现代通信系统中是必不可少的,但是如果直放站的收发天线隔离度不够,整机增益偏大时,输出信号经延时后反馈到输入端,会使直放站输出信号发生严重失真产生自激。在无线通信系统的同频直放站中,为了减小产品体积以及缩短建站成本,收发天线常常放置在一起(或距离很近)。由于收发天线往往只存在方向角的不同,因此直放站的接收天线肯定会接收到其转发天线所发送的经过放大的信号,而对所期望接收的有用信号产生干扰。如果不对干扰信号进行处理,干扰和期望信号的叠加信号会再次被送进功放,再进行放大转发,干扰信号的强度会一直积累,最终使得直放站无法正常工作。这种正反馈式干扰(干扰信号与正常通信信号的调制参数和载波频率是完全一致的,使得接收机收到叠加有同频干扰的混合信号)还会对数字通信产生严重的电磁干扰,从而阻碍正常的通信。在上、下行链路中,往往都存在着这种反馈式干扰,如图1所示。
干扰抵消是同频直放站所必备的一项技术,也是信号处理领域一个非常重要的课题[1]。传统上,克服自激现象的方法有:(1)借助建筑物阻挡在发射和接收天线间; (2)增加直放站的施主和重发天线的空间隔离度。垂直隔离度一般最好大于1m,水平隔离度可以在十几米以上。如果没有垂直隔离的话,那么水平隔离的距离几乎达到200米;(3)降低直放站的增益:上行和下行按照比例,就是上下行链路平衡,直至消除自激。
虽然上述三种办法都可以在一定程度上降低干扰的影响,但是在某些场合,受到环境或系统性能的要求,这些方法并不可行。因此,利用自适应干扰抵消器来减少直放站设备的同频反馈干扰成为首选方案。在所有的自适应方案中,尤以频域算法在性能和复杂度之间取得良好平衡。
本项目以WCDMA系统为例,讨论数字频域自适应干扰抵消技术的实现,并从功率谱密度和星座图以及误差向量幅度(EVM)等性能指标对方案进行评价。在设计中,为了验证算法性能且保证接收端的正常工作,同时实现了WCDMA小区搜索的三步同步过程,并通过PC机对输入输出数据进行比对分析,验证方案性能。
系统方案
完整的系统从数字下变频后的基带数据开始,至数字上变频的前端为止,包括系统同步和干扰抵消两大组成模块,系统框图如图2所示,其简要介绍如下:
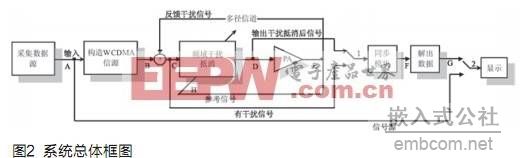
(1)在没有干扰的情况下,所采集的数据源从A点输入,然后将其构造为WCDMA信源,作为频域干扰抵消模块的输入。为了使干扰抵消模块正确运转,在本设计中的B点输出信号为每个码片4采样。
(2)为体现频域干扰抵消的作用,在系统中必须模拟一个干扰信号。本设计将D点的输出经过功放(PA)作为干扰信号。
(3)将干扰信号经过多径信道,反馈到B点与WCDMA信号叠加,再进入干扰抵消模块。为了抵消干扰,将E点的输出反馈到干扰抵消模块作为参考信号。在下文中,将此反馈支路称为辅链路;而干扰抵消+功放的链路称为主链路。
(4)有干扰的信号经过频域干扰抵消模块,输出抵消后的无干扰信号给同步模块,即D点。同步模块进行三步搜索,得到帧头以及扰码信息。对同步后的码片信号进行解扰解扩后得到信息数据,如图中G点输出。
(5)在开关1处,可以选择:有干扰的信号(C点)或者干扰抵消后的信号(D点)输入同步模块,并输出显示。
(6)在开关2处,可以选择:数据源直接显示(A点),或者是同步后解出的数据显示(G点)。
算法设计
频域自适应干扰抵消(AIC)模块利用了频域实现的LMS算法[2,3]。该算法通过1/2重叠保留法的快速傅立叶变换(FFT),在频域以直接相乘的计算方式实现快速相关和快速卷积[4]。算法基本框图如图3,其中A点为被干扰的信号,B为反馈链路的信号,C点为干扰被抵消后的输出。主要包括以下循环执行的操作流程,其中k表示第个k数据块:
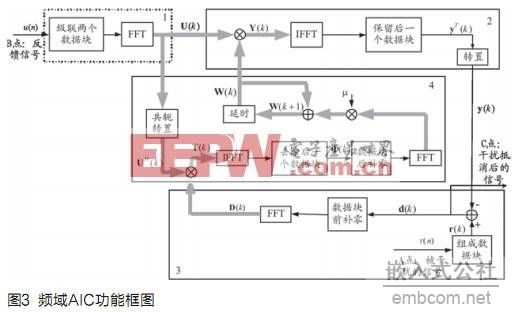
(1)对自适应滤波器的M个频域抽头系数W(k)作初始化设置;
(2)将滤波器的时域连续输入信号u(n)每个M组成一个块,然后级联两个数据块做N点离散快速傅立叶变换,使其转换为频域信号U(k),并将此信号用作自适应滤波器的输入;其中N是该滤波器抽头个数M的2倍,即N=2M;
(3)将U(k)通过滤波器得到输出信号Y(k),然后进行快速傅立叶逆变换(IFFT)处理,使其转换为时域信号y(k),作为干扰的估计值;
(4)计算被干扰信号r(k)和y(k)的差值,即为干扰抵消后的信号d(k);再产生该期望信号的频域值D(k)为下一次滤波器抽头系数迭代所使用;
(5)利用频域信号进行最小均方误差LMS计算,即根据D(k)和U(k)对W(k)进行更新,并将此更新值返回到步骤(2)中使用。跳转到步骤(2)进行反复迭代,直至干扰被抵消。
与传统的时域LMS算法相比,利用频域LMS算法可以降低计算复杂度。假设输入为实信号,滤波器抽头个数为。可以得到,频域LMS和时域LMS的计算复杂度之比为

。实际中,干扰在空中传输的时延会比反馈信号的时延大得多,这时需要较大的抽头个数才能抵消干扰。假设M=1024,则频域LMS算法可以比时域LMS算法的速度提高大约16倍。为简化起见,在本文档中取M=64,利用频域LMS算法,在计算量角度大约可以比时域LMS算法快1.5倍。
电子 滤波器 PIC 仿真 FPGA DAC 赛灵思 ModelSim 相关文章:
- 变革电信网网络安全框架 (01-03)
- 浅谈IPv6技术的若干问题(01-09)
- LG电子低成本CDMA手机的设计原则剖析 (01-12)
- 专家教你做个病毒高手(04-30)
- 数据库归档要考虑的四大问题(05-26)
- 5个步骤成功加密电子邮件(07-18)
