PLL锁相环的基本结构及工作原理

振荡频率应随输入控制电压线性地变化。它输出的信号根据锁相环的不同要求，可分为正弦波压控振荡器与非正弦波压控振荡器两大类。

　　正弦波压控振荡器一般由LC点式振荡器与变容二极管组成．它的工作原理与计算公式和电容三点式正弦波振荡器完全一样。由于正弦波VCO受到变容二极管结电容变化范围的限制，因此一般振荡频率变化范围都不是太大。非正弦波压控振荡器的种类较多，由于它的频率变化范围大，控制线性好，所以应用比较广泛。这类压控振荡器常见的几种电路有射极定时压控多谐振荡器、积分型施密特压控振荡器、数字门电路压控振荡器。

　　图为两种方波压控振荡器电路。

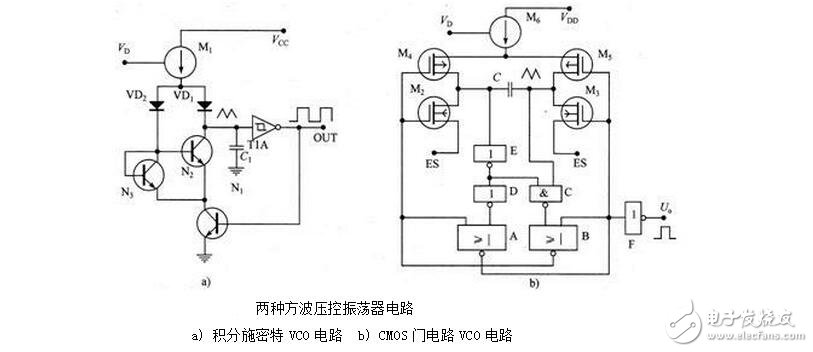
　　三．环路滤波器

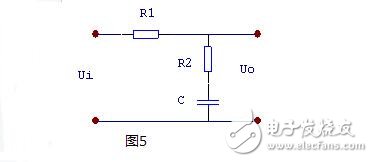
　　这里仅讨论无源比例积分滤波器如图5。其传递函数为：

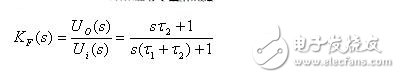
　　式中：τ1 = R1 C

　　τ2 = R2 C

　　图为目前比较常用的三种环路滤波器电路。从图中可以看出，三种电路的复杂程度不一样。第一种简单的RC滤波器所用元件最少，电路也最简单。有源比例积分滤波器，使用 元件最多，电路也比较复杂。

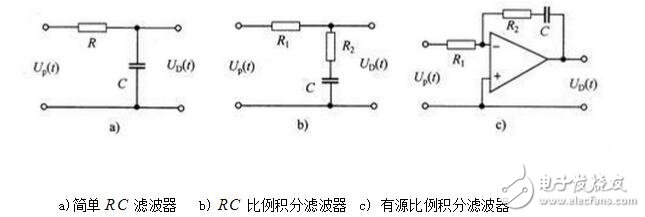
　　但从滤波效果的角度来衡量，有源比例积分滤波器的滤波效果最好，简单RC滤波器滤波效果最差，RC比例积分滤波器的滤波效果介于二者之间。设计电路时，可以根据锁相环路的要求选择不同的环路滤波器。

　　四．锁相环的相位模型及传输函数

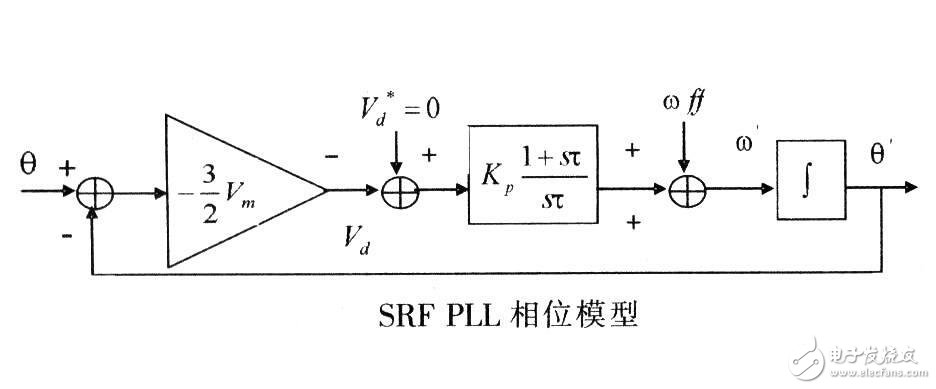
　　图为锁相环的相位模型。要注意一点，锁相环是一个相位反馈系统，在环路中流通的是相位，而不是电压。因此研究锁相环的相位模型就可得环路的完整性能。

　　由图6可知：

　　（1）当A点断开环路时，锁相环的开环相位传输函数为

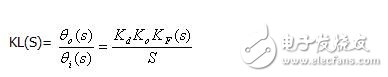
　　（2）环路闭合时的相位传输函数为

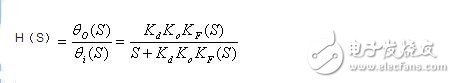
　　（3）环路闭合时的相位误差传输函数为

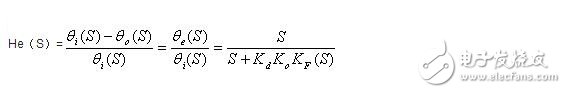
　　当环路滤波器选用无源比例积分滤波器时，经推导可得：

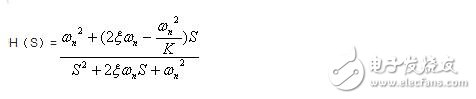
　　式中

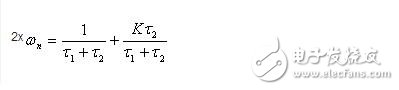
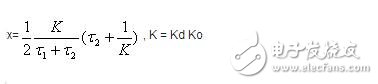
　　同样可得：

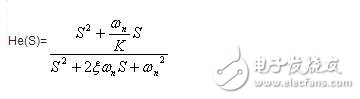
　　ωn称为系统的固有频率或自然角频率；

　　x 称为系统的阻尼系数。

　　要注意的是上面讨论中的ω指的是输入信号相位的变化角频率，而不是输入信号本身的角频率。如输入信号是调频信号，则ω指的是调制信号的角频率而不是载波的角频率。

　　五．锁相环的同步与捕捉

　　锁相环的输出频率（或VCO的频率）ωo能跟踪输入频率ωi的工作状态，称为同步状态，在同步状态下，始终有ωo = ωi。在锁相环保持同步的条件下，输入频率ωi的最大变化范围，称为同步带宽，用DωH 表示。超出此范围，环路则失锁。

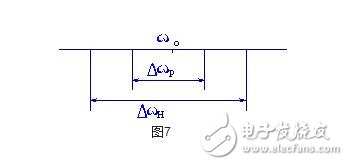
　　失锁时，ωo≠ωi，如果从两个方向设法改变ωi，使ωi向ωo靠拢，进而使Δωo =（ωi－ωo）↓，当Δωo小到某一数值时，环路则从失锁进入锁定状态。这个使PLL经过频率牵引最终导致入锁的频率范围称为捕捉带Δωp。同步带ΔωH，捕捉带Δωp 和VCO 中心频率ωo的 关系如图7。