时钟抖动时域分析(中)

　　引言

　　本系列文章共三个部分，第1部分重点介绍了如何准确地估算某个时钟源的抖动，并将其与ADC的孔径抖动组合。在本文即第2部分中，这种组合抖动将用于计算ADC的信噪比 (SNR)，之后将其与实际测量情况进行比较。

　　滤波采样时钟测量

　　我们做了一个试验，目的是检查测得时钟相位噪声与提取自ADC测得SNR的时钟抖动的匹配程度。如图11所示，一个使用Toyocom 491.52-MHz VCXO的TI CDCE72010用于产生122.88-MHz采样时钟，同时我们利用Agilent的E5052A来对滤波相位噪声输出进行测量。利用一个SNR主要受限于采样时钟抖动的输入频率对两种不同的TI数据转换器(ADS54RF63和ADS5483)进行评估。快速傅里叶变换 (FFT) 的大小为131000点。

　　图11 滤波后时钟相关性测试装置结构

　　图12所示曲线图描述了滤波后CDCE72010 LVCMOS输出的测得输出相位噪声。131000点的FFT大小将低积分带宽设定为~500Hz。积分上限由带通滤波器设定，其影响在相位噪声曲线图中清晰可见。超出曲线图所示带通滤波器限制的相位噪声为E5052A的噪声底限，不应包括在抖动计算中。滤波后相位噪声输出的积分带来~90 fs的时钟抖动。

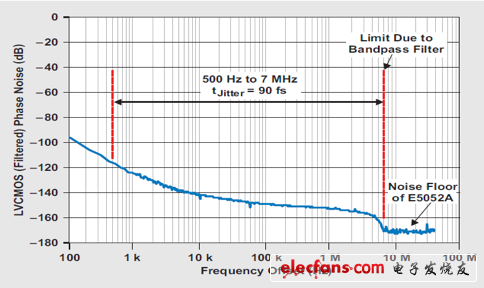
　　图12 滤波后时钟的测得相位噪声

　　接下来，我们建立起了热噪声基线。我们直接从~35 fs抖动的时钟源生成器使用滤波后采样时钟对两种ADC采样，而CDCE72010被绕过了。将输入频率设定为10MHz，预计对时钟抖动SNR无影响。然后，通过增加输入频率至SNR主要为抖动限制的频率，确定每个ADC的孔径抖动。由于采样时钟抖动远低于估计ADC孔径抖动，因此计算应该非常准确。另外还需注意，时钟源的输出振幅应会增加(但没有多到超出ADC的最大额定值)，从而升高时钟信号的转换率，直到SNR稳定下来为止。

　　我们知道时钟源生成器滤波后输出的外部时钟抖动为~35 fs，因此我们可以利用测得的SNR结果，然后对第1部分(请参见参考文献1)中的方程式1、2和3求解孔径抖动值，从而计算得到ADC孔径抖动，请参见下面的方程式4。表3列举了每种ADC测得的SNR结果以及计算得孔径抖动。

　　表3 测得的SNR和计算得抖动

　　利用ADC孔径抖动和CDCE72010的采样时钟抖动，可以计算出ADC的SNR，并与实际测量结果对比。使用ADC孔径抖动可以通过测得SNR值计算出CDCE72010的采样时钟抖动，如表4所列。乍一看，预计SNR值有些接近测得值。但是，将两种ADC计算得出的采样时钟抖动与90fs测得值对比时，出现另一幅不同的场景，其有相当多的不匹配。

　　不匹配的原因是，计算得出的孔径抖动是基于时钟源生成器的快速转换速率。CDCE72010的LVCMOS输出消除了时钟信号的高阶谐波，其有助于形成快速升降沿。图13所示波形图表明了带通滤波器急剧降低未滤波LVCMOS输出转换速率，以及将方波转换为正弦波的过程。

　　图13 时钟抖动对采样时钟转换速率的影响

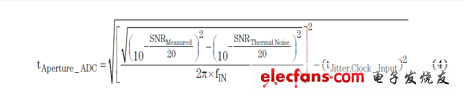
　　表4 90-fs时钟抖动的SNR结果

　　 改善转换速率的一种方法是：在CDCE72010的LVCMOS输出和带通滤波器之间添加一个具有相当量增益的低噪声RF放大器，参见图14。该放大器应该放置于滤波器前面，这样便可以将其对时钟信号的噪声影响程度限定在滤波器带宽，而非ADC的时钟输入带宽。由于下一个试验的放大器具有21dB的增益，因此我们在带通滤波器后面增加了一个可变衰减器，旨在匹配滤波后LVCMOS信号到时钟生成器滤波后输出的转换速率。该衰减器可防止ADC的时钟输入超出最大额定值。

　　图14 带通滤波器前面添加RF放大器来降低转换速率

　　通过在时钟输入通路中安装低噪声RF放大器，两个数据转换器重复进行了高输入频率的SNR测量，其结果如表5所示。我们可以看到，测得SNR和预计SNR匹配的非常好。使用下面的方程式 5，计算得到的时钟抖动值在90-fs时钟抖动的5fs以内，其结果通过相位噪声测得推导得出。

　　表5 90-fs时钟抖动和RF放大器的SNR结果

　　未滤波采样时钟试验

　　为了强调滤波采样时钟的重要性，在下一个试验中，我们将时钟带通滤波器从CDCE72010输出端去除。在图15所示结构中，我们使用了E5052A相位噪声分析仪来捕获时钟相位噪声。但是不幸的是，该分析仪对相位噪声的测量仅达到40-MHz载波频率偏移，并且在这点以外没有给出任何相位噪声特性的相关信息。

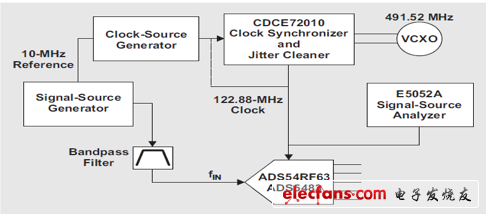
　　图15 未滤波采样时钟输入的测试装置结构

要设定使用未滤波时钟时的正确积分上限，我们必须再一次复习一下采样理论。CDCE72010的未滤波时钟输出看起来像一种具有快速升降沿的方波，而其升降沿由时钟频率的基频正弦波高阶谐波引起。这些谐波的振