控制系统的时域分析法--高阶系统的暂态响应

控制系统的时域分析法--高阶系统的暂态响应

当系统高于二阶时，将其称为高阶系统。其传递函数一般可以写成如下形式

将上式进行因式分解，可写成

式中 si：传递函数极点，i=1、2、…、n；
zj：传递函数极点，j=1、2、…、m。

假定系统所有零点、极点互不相同，并假定极点中有实数极点和复数极点，而零点中只有实数零点。当输入为单位阶跃函数时，其阶跃响应的象函数为

=++

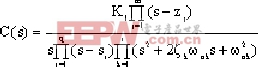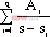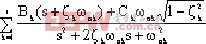式中 m：传递函数零点总数；
n：传递函数极点总数，n=q+2r；
q：实极点数；
r：共轭复数极点的对数。

对上式求取原函数，即得高阶系统的单位阶跃响应：

c(t) = A ++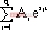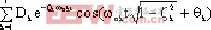

式中 Ai =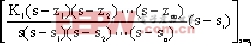

Dk =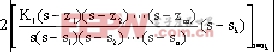

θk=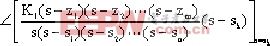

sk=-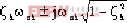

由此可见，高阶系统的暂态响应是一阶和二阶系统暂态响应分量的合成。可以得到如下结论：

1.高阶系统暂态响应各分量的衰减快慢由指数衰减系数si及 决定。假设系统的一对复数极点与虚轴间距离为 ，另一对复数极点与虚轴间距离是其5倍，即5 ，如按式（3-15）估算，后者对应的暂态分量衰减时间大约为前者的1/5，由此可知，系统的极点在s平面左半部距虚轴愈远，相应的暂态分量衰减得愈快。

2. 高阶系统暂态响应各分量的系数Ai和Dk不仅与s平面中极点的位置有关，并且与零点的位置也有关。当某极点si愈靠近某一零点zj而远离其他极点，同时与s平面的原点相距也很远，则相应分量的系数Ai越小，该暂态分量的影响就小。若一对零、极点互相接近，则该极点对暂态响应几乎没有影响。极端情况，若一对零、极点重合（偶极子），则该极点对暂态响应无任何影响。若某极点si远离零点，但距S平面原点较近，则相应的该分量的系数Ai就比较大，于是，该分量对暂态响应的影响就较大。因此，对于系数很小的分量以及远离虚轴的极点对应的衰减很快的暂态分量常可忽略，于是高阶系统的响应就可以用低阶系统的响应去近似。

3. 如果高阶系统中距离虚轴最近的极点，其实部比其他极点的实部的1/5还要小，并且该极点附近没有零点，则可以认为系统的响应主要由该极点决定。这些对系统响应起主导作用的极点，称为系统主导极点。高阶系统的主导极点常是共轭复数极点。如能找到一对共轭复数主导极点，则高阶系统就可以近似地当作二阶系统来分析，相应地其暂态响应性能指标都可以按二阶系统来近似估计。

在设计一个高阶系统的时候，常利用主导极点这一概念选择系统参数，使系统具有预期的一对共轭复数主导极点，这样就可以近似地用二阶系统的性能指标来设计系统。详见后面有关系统设计章节的内容。