基于FPGA的语音端点检测

语音端点检测就是从背景噪声中找到语音的起点和终点，其目标是要在一段输入信号中将语音信号同其他信号(如背景噪声)分离并且准确地判断出语音的端点。研究表明，即使在安静的环境中，一半以上的语音识别系统识别错误来自端点检测。因此，端点检测的重要性不容忽视，尤其在噪声环境下语音的端点检测，它的准确性很大程度上直接影响着后续的工作能否有效进行[1]。

当前语音识别系统大多以ARM、DSP为设计核心，其设计费用高、缺乏灵活性、开发周期长，而且很难满足高速的系统要求。在对语音端点检测算法的研究中，提出了诸如基于能量、过零率、LPC预测残差等多种算法[2]，但这些方法大部分都是基于计算机软件的，不适合进行硬件开发[3]。

FPGA具有功耗低、体积小、速度快等优点，可以满足语音识别系统的实时性要求。本文尝试用FPGA实现语音端点检测，对常用的Lawrence Rabiner端点检测法进行改进，用纯硬件的方法实现语音端点检测，并以"长沙"等词和短语为例，验证其准确性和可行性。

1 FPGA实现语音端点检测基本原理

主要由四个部分完成：预加重、分帧、加窗和端点判断，FPGA实现方法同样要经过这四个步骤。

1.1 预加重

语音信号的平均功率谱由于受声门激励和口鼻辐射的影响，高频端大约在800 Hz以上按6 dB/Oct(倍频程)衰减，这样语音信号的频谱中，频率越高相应的成分越少，因而要得到高频部分的频率比低频部分更困难。所以，对语音信号进行分析之前，要对语音信号加以提升，使语音信号的短时频谱变得更为平坦，从而便于进行频谱分析和声道参数分析。提升的方法有模拟电路法和数字电路法，本设计主要采用数字电路法。一般的数字电路法用一阶的数字滤波器来实现：

式(2)只有移位和加减运算，即用简单的移位来取代复杂的小数乘法运算，从而可以方便地用FPGA实现。

1.2 分帧加窗

分帧处理即将预加重后的语音信号分成多段进行分析，即从原始语音序列中分解出一个新的依赖于时间的序列，便于描述语音信号特征。语音信号具有时变特性，但在相当短的时间范围内，其特性基本保持不变，从而可以进行分段分析。假设语音信号在10 ms～30 ms内平稳，就可以以此时间段为单位将语音信号分ms段进行分析，其中每一段称为一"帧"，每一帧的长度叫帧长。为了使帧与帧之间保持连续平滑过渡，分帧一般采用交叠分段的方法，前一帧和后一帧的交叠部分称为帧移。帧移与帧长的比值一般取为0～1/2。为便于语音识别系统中特征的提取，取2n为帧长。本文语音信号的采样频率为16 kHz，取帧长为256(16 ms)，帧移为128。

分帧的FPGA实现。其关键就是解决帧移的叠加问题。可以用两个FIFO(F1和F2)来实现，具体过程为：先向F1写入128个数;读取F1中的数得到这帧前128个数，同时将F1中的数写入F2中;F1的数读完时F2也已写完，此时再读取F2中的数得到这帧的后128个数(这时就得到了一帧的语音信号)，在读取F2中数据的同时向F1写入下一帧的数据，这样一直循环就完成了语音的分帧。

分帧后帧之间重新拼接处语音信号的频谱特性和原来相比会有差异。为了使语音信号在帧之间重新拼接处的频谱特性与原来更加接近，就要进行加窗处理。在语音信号处理中常用的窗函数是矩形窗和汉明窗[5]。它们的表达式如下(其中N为帧长)：

矩形窗：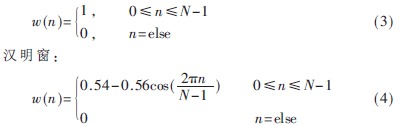

矩形窗的主瓣宽度较小，因而具有较高的频率分辨率;但它的旁瓣峰值较大，因此其频谱泄露比较严重。相比较而言，虽然汉明窗主瓣宽度较矩形窗大一倍，但是它的旁瓣衰减较大，因而具有更平滑的低通特性，能够在较高程度上反映短时语音信号的频谱特性，所以本文采用汉明窗。

加窗的FPGA实现。加窗就是用分帧后的数据乘以窗函数。在FPGA的实现上加汉明窗的过程难点是小数余弦乘法运算，如果用算法来实现运算会比较慢。这里考虑到N比较小，可以采用查表法实现加窗处理。查表法就是将窗函数的各个值存在ROM里面，依次查找。这里用DSP Builder工具生成窗函数的各个值，因为Altera公司开发的DSP Builder工具有很强的数字信号处理功能，能很好地完成窗函数的运算。具体操作步骤为：在Matlab中打开simulink工具并打开Altera DSP Builder Blockset工具箱，然后新建".mdl"文件，在工具箱中找到相应的模块并连接。在"hamming_table"模块的"Matlab Array"中输入"0.54-0.56*cos([0:2*pi/255:2*pi])"。然后编译、综合，系统就会自动生成查表法要用到的".hex"文件。

1.3 端点判断

端点判断是整个端点检测中最重要的部分，也是计算量最大的部分。所以算法的选择非常重要，本文用算法是根据Lawrence Rabiner端点检测法改进而来的