利用热分析预测IC的瞬态效应并避免过热
直流工作模式下,往往能够利用数据资料提供的参数确定结温,例如θJA (热阻)和θJC (结温热特性)1。然而,为了预测直流模式以外的结温峰值达到多高(例如,由PWM信号驱动的功率MOSFET,用于控制LED或开关稳压器),需要了解瞬态热特性数据。尽管该数据非常有用,但通常情况下数据资料并未提供这些数据。您可能还需要了解芯片在给定功率耗散水平下能够工作多长时间而不发生故障。这个问题也很难回答。
本文解决了利用功耗和环境温度预测芯片结温的问题,芯片结温是时间函数。本文首先引入分析方法所依据的物理定律。然后将IC系统定义为一个复杂的分层热体模型进行讨论。进而对热体模型进行理论分析,并得出瞬态热性能的表达式。本文根据这些公式提出了一种等效的RC无源网络,用于表示IC的热特性。最后,为了证明这一分析方法的有效性和准确性,文章给出了具有PWM调光功能的高电压线性HB LED (高亮度LED)驱动电路MAX16828的实验结果。
热力学定律
对于任何物体,均可通过以下两个基本定律得到温度与时间的关系式。
牛顿冷却定律:
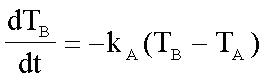 (式1)
(式1)
其中: TB为物体温度,TA为环境温度。kA为比例常数(>0)。 t为时间。
根据能量守恒定律:
mcΔT = 能量 = PΔt (式2)
其中: P为热源产生或传递给热源的恒定功率。m为发热体质量。 c为特定物体的热容量。
结合这两个定律,我们得到:
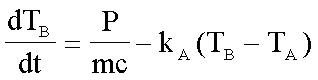 (式3)
(式3)
IC的数据资料通常列出了封装的热特性数据,例如θJA。我们利用该数据可以分析封装的稳态热平衡,从而检查是否满足式3:

其中: θBA为热阻--物体至环境。 TB为封装内温度。 TA为外部环境温度。
故: 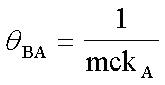 (式6)
(式6)
将芯片定义为一个热系统
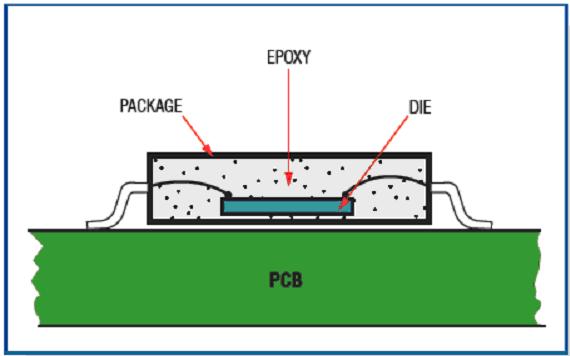
清晰地定义系统非常重要,因为热分析结果依赖于这一定义。从安装在PCB的芯片横截面(图1),我们可以看到管芯到环境通道至少有三种不同材料:管芯本身、环氧树脂铸模和封装。根据主要热源的位置不同,热模型基于两种热流动模式之一:从外部热源至管芯(当外部热源是主要热源时)和从管芯至外部环境(当管芯为主要热源时)。我们就这两种模式分别进行讨论。
从外部热源至芯片的热流动
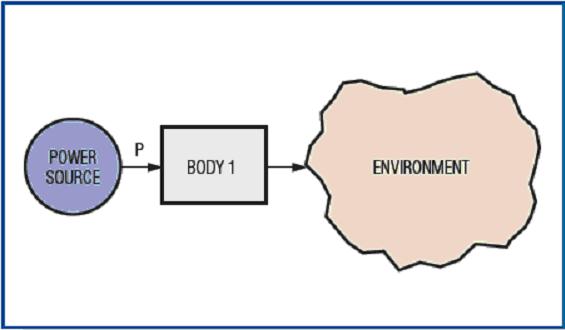
考虑图2所示系统,该图给出了一个均匀物体从电源获得能量(热量)并向外部环境释放能量的示意图。
热量通过封装和铸模复合物到达内部管芯。所以,该系统也模拟了热源处于封装外部时芯片的瞬态热特性。由于管芯具有很多金属,封装热阻通常比管芯本身高得多。因此,管芯温度随着封装温度的变化而改变,几乎没有滞后,使芯片看起来像个整体。我们可以利用式3定义这一整体系统。求解TB,得到: 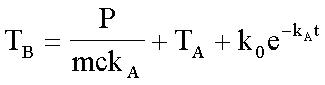 (式7)
(式7)
其中,k0为积分常数,由初始条件求解得到。一般而言,该式对于热源处于芯片外部情况下定义芯片的瞬态热特性非常有用。
可以通过一个实例解释这一模型。确定芯片的瞬态热特性,其初始温度为Ti,式7中带入t = 0,TB = Ti: 
式11和式12在热源处于封装外部情况下,对于预测芯片温度(无论是封装还是管芯)非常有用。需要耗散大量热量的大电流MOSFET附近就是一个热源特例。
已知kA和θJA,即可计算出不同时间的温度。或者,如果P为时间的复合函数,即可利用以上公式作为时间仿真来评估温度,并利用MATLAB®软件编程绘制温度随时间变化的函数。θJA由数据资料提供。但是,如果某项配置条件与JEDEC标准规定不同,利用公布的θJA值进行计算会产生误差。JEDED标准51-3节指出:"值得强调的是,利用这些测试板测试得到的数值不能用于直接预测任何具体应用系统的性能,只能用于封装之间的比较"2。所以,为了正确估算温度,应该针对原型开发板测量θJA值,或按照下列说明直接估算。
从管芯至环境的热流动
考虑图3所示的三体系统(与芯片相似),在管芯处产生热量并通过环氧树脂和封装将热量耗散至外部环境。组件1为管芯,组件2为环氧树脂,组件3为芯片封装。
为了求解该系统中的θJA,我们必须为三个物体定义公式。

其中:
TB1、TB2和TB3分别是组件1、2和3的瞬时温度;P12是以热形式从组件1传导至组件2的功率;P23是以热形式从组件2传导至组件3的功率;PG是组件1直接产生的功率,或直接传导至组件1的功率。管芯产生的功率(PG)减去管芯吸收的功率,得到:

从式18、式19和式20求解三体系统比较复杂,但利用拉普拉斯变换可以简化计算。求解公式为:
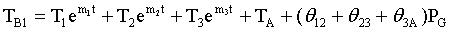 (式21)
(式21) 其中:
θ12为组件1至组件2的热阻;θ23为组件2至组件3的热阻;θ3A为组件3至环境的热阻;T1、T2和T3为积分常数;m1、m2和m3为k1、k2和k3的函数。
管芯产生功耗时,式21能够以非常准确的方式预测管芯温度。然而,使用该式时,我们必须知道所有积分常数以及m1、m2和m3,它们为复杂函数,求解非常困难。为了避开这种困难操作,我们利用一个工具求解不同方程:SPICE。
