利用热分析预测IC的瞬态效应并避免过热
时间：01-02
来源：Maxim Integrated Products技术专家Milind Gupta
点击：
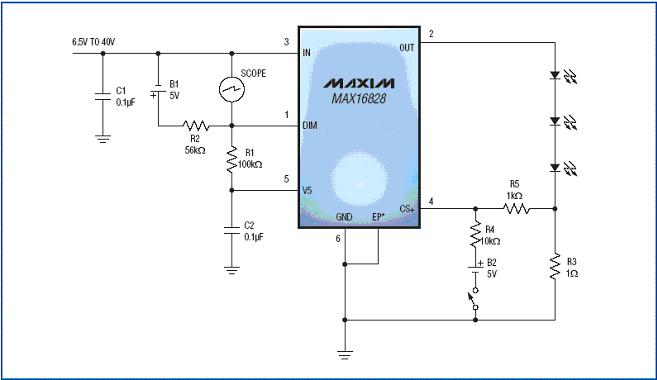
图6. MAX16815/MAX16828 HBLED驱动器的典型应用电路。
这种状态下，元件承载大量电流，ESD二极管测量处于测量通路。因此，由于焊接线和内部金属电阻的影响，会产生一定误差。根据内部布局和焊接线长度计算，估计最差情况下的寄生电阻为50mΩ。200mA下，该寄生电阻会在二极管读数上产生大约±10mV (最大)的误差，对应的温度测量精度误差大于±5°C。此外，管芯ESD二极管放置在靠近片上功率MOSFET和热保护电路处。这种配置可使二极管更准确地表示该区域的温度。
系统定义1
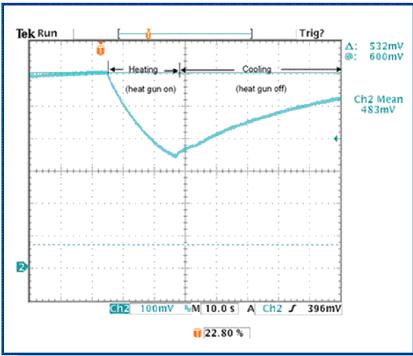
接下来的部分介绍如何利用测试装置，采集代表瞬时热特性的二极管电压，用于上述式7和式21的系统定义方程式。为了计算kA和θJA (代入式11)，采用热风枪加热芯片。因为我们并不希望芯片内部产生热量，所以将芯片断电。利用热风枪加热元件会使封装、管芯的温度上升。可利用示波器测量二极管的电压，以监测管芯的温度变化(图 8)。
当芯片加热时，二极管电压按照指数规律迅速下降，与公式预测结果一致。接近曲线中间位置时，关闭热枪，使封装和管芯开始冷却。二极管电压又按照指数规律上升。我们并不确切知道有多少热量从热风枪传递到芯片。因此，为了消除该未知数，我们首先将式28调整为仅拟合曲线(图8)的上升部分(冷却)。这种曲线拟合使我们能够估算kA的最佳值。冷却期间没有热功率传递至封装，封装仅仅进行冷却，P = 0。因此，式28可简化为：
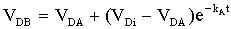(式34)
我们已知VDA (室温下的初始测量值为643mV)和VDi (t = 0时的参考读数)值。为了确定KA，我们必须调整方程式，使其包括上升曲线的一对读数，将得到kA = -0.0175。图9所示为采用上述kA值时的读数(二极管电压单位为mV，与以秒为单位的时间的对应关系)和式34的波形。
正如我们在图9中看到的那样，式34与kA = -0.0175时的测量数据非常接近。为了验证我们公式的正确性，我们尝试利用针对kA测定的值拟合公式28的下降曲线，方程式精确拟合(图10)。因此，我们看到针对系统定义1所讨论系统的式34与实验数据非常接近。
系统定义2
验证系统2的式30、式31和式32更加困难。必须在管芯产生热量，利用二极管正向电压测量管芯温度，并将温度值与提出的RC网络的C1电压仿真数据进行拟合。这项工作可利用MATLAB编程实现。在已知整个芯片初始温度的情况下，记录不同时间的瞬态热特性非常重要。按照这种方式，我们还可以求解RC网络的初始电容电压。利用相同的测试装置(参见图7)，接通电流通道并在示波器上采集二极管电压(图11)。
记录三种不同耗散功率下的瞬态电压，用一条曲线模拟这些数据。图12所示曲线是第一组数据的拟合结果，此时功耗为1.626W；图13所示波形是实测数据与仿真数据的比较。同样，图14所示波形说明了RC网络对第二组读数(耗散功率为2.02W)的仿真；图15所示波形说明了对第三组读数(耗散功率为1.223W)的仿真情况。
实验结果表明实测结果与理论模型非常吻合。一旦针对具体芯片构建RC网络模型，这种模型将对仿真IC的瞬态温度非常有用。模型亦可用于类似尺寸的芯片，确定其定义阶段的热特性。利用这种方式可以表示芯片的工作范围限制，反过来，这些信息也能够帮助定义芯片的工作模式，以避免过热。
结论
本文介绍了通过RC网络仿真芯片热特性的方法，然后可以利用SPICE工具方便地进行仿真。以下方法有助于提高该模型的精度：
获取极端功耗条件和中等水平下的数据。将RC网络同时拟合到三个不同状况，使模型复合绝大多数实际功耗的要求。
通过在不同环境温度下采集数据提高模型精度。
这种状态下，元件承载大量电流，ESD二极管测量处于测量通路。因此，由于焊接线和内部金属电阻的影响，会产生一定误差。根据内部布局和焊接线长度计算，估计最差情况下的寄生电阻为50mΩ。200mA下，该寄生电阻会在二极管读数上产生大约±10mV (最大)的误差，对应的温度测量精度误差大于±5°C。此外，管芯ESD二极管放置在靠近片上功率MOSFET和热保护电路处。这种配置可使二极管更准确地表示该区域的温度。
系统定义1
接下来的部分介绍如何利用测试装置，采集代表瞬时热特性的二极管电压，用于上述式7和式21的系统定义方程式。为了计算kA和θJA (代入式11)，采用热风枪加热芯片。因为我们并不希望芯片内部产生热量，所以将芯片断电。利用热风枪加热元件会使封装、管芯的温度上升。可利用示波器测量二极管的电压，以监测管芯的温度变化(图 8)。
当芯片加热时，二极管电压按照指数规律迅速下降，与公式预测结果一致。接近曲线中间位置时，关闭热枪，使封装和管芯开始冷却。二极管电压又按照指数规律上升。我们并不确切知道有多少热量从热风枪传递到芯片。因此，为了消除该未知数，我们首先将式28调整为仅拟合曲线(图8)的上升部分(冷却)。这种曲线拟合使我们能够估算kA的最佳值。冷却期间没有热功率传递至封装，封装仅仅进行冷却，P = 0。因此，式28可简化为：
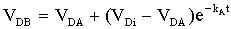(式34) 我们已知VDA (室温下的初始测量值为643mV)和VDi (t = 0时的参考读数)值。为了确定KA，我们必须调整方程式，使其包括上升曲线的一对读数，将得到kA = -0.0175。图9所示为采用上述kA值时的读数(二极管电压单位为mV，与以秒为单位的时间的对应关系)和式34的波形。
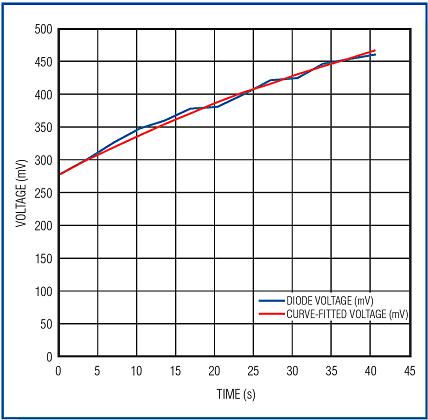
正如我们在图9中看到的那样，式34与kA = -0.0175时的测量数据非常接近。为了验证我们公式的正确性，我们尝试利用针对kA测定的值拟合公式28的下降曲线，方程式精确拟合(图10)。因此，我们看到针对系统定义1所讨论系统的式34与实验数据非常接近。
系统定义2
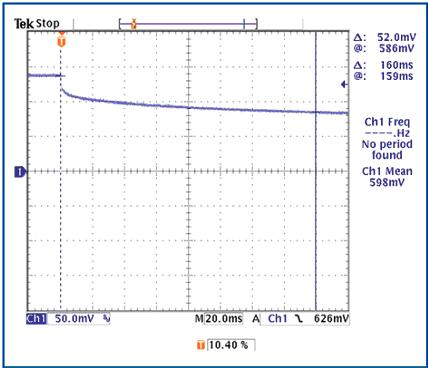
验证系统2的式30、式31和式32更加困难。必须在管芯产生热量，利用二极管正向电压测量管芯温度，并将温度值与提出的RC网络的C1电压仿真数据进行拟合。这项工作可利用MATLAB编程实现。在已知整个芯片初始温度的情况下，记录不同时间的瞬态热特性非常重要。按照这种方式，我们还可以求解RC网络的初始电容电压。利用相同的测试装置(参见图7)，接通电流通道并在示波器上采集二极管电压(图11)。
记录三种不同耗散功率下的瞬态电压，用一条曲线模拟这些数据。图12所示曲线是第一组数据的拟合结果，此时功耗为1.626W；图13所示波形是实测数据与仿真数据的比较。同样，图14所示波形说明了RC网络对第二组读数(耗散功率为2.02W)的仿真；图15所示波形说明了对第三组读数(耗散功率为1.223W)的仿真情况。
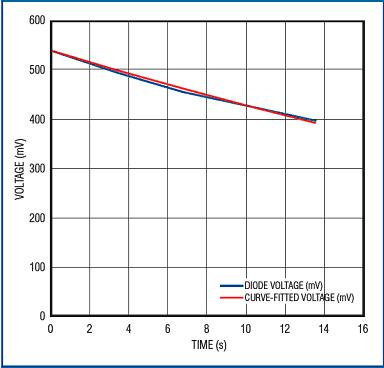
实验结果表明实测结果与理论模型非常吻合。一旦针对具体芯片构建RC网络模型，这种模型将对仿真IC的瞬态温度非常有用。模型亦可用于类似尺寸的芯片，确定其定义阶段的热特性。利用这种方式可以表示芯片的工作范围限制，反过来，这些信息也能够帮助定义芯片的工作模式，以避免过热。
结论
本文介绍了通过RC网络仿真芯片热特性的方法，然后可以利用SPICE工具方便地进行仿真。以下方法有助于提高该模型的精度：
获取极端功耗条件和中等水平下的数据。将RC网络同时拟合到三个不同状况，使模型复合绝大多数实际功耗的要求。
通过在不同环境温度下采集数据提高模型精度。
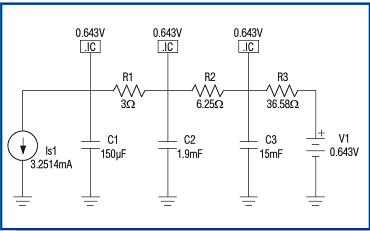
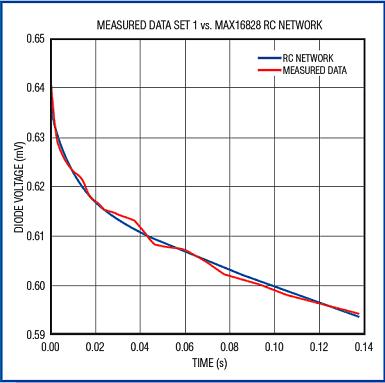
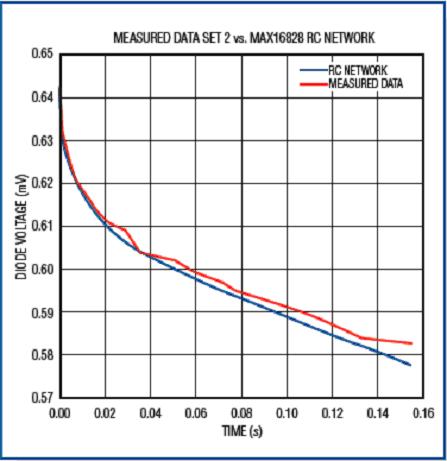
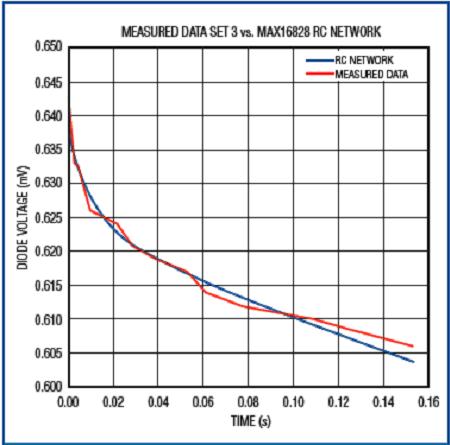图15. 当管芯耗散功率为1.223W时，芯片加热曲线