基于改进的小波神经网络的汽车电控汽油机故障诊断
时间:07-30
来源:作者:王瑞云 李华
点击:
0 引言
汽车电控汽油机故障诊断是通过研究故障征兆(特征向量)之间的关系来判断设备故障的。汽车电控汽油机故障诊断形式多种多样,故障产生的机理也非常复杂,加之实际因素的复杂性,故障与征兆之间表现出一种非常复杂的关系,即各类故障所反映的特征参数并不完全相同,这种关系很难用精确的数学模型来表示,这给现场诊断带来了极大的困难。由于人工神经网络具有高度的并行处理能力和极强的非线性映射能力,可以实现故障与征兆之间的非线性映射关系,因此在汽车电控汽油机故障诊断领域中显示了很大的应用潜力。其中用得最多的是基于Sigmoid输出函数的BP网络,尽管基于BP神经网络的故障诊断方法有许多优点,比如自学习能力强,不需要输入输出之间具体关系以及具有好的模型分类能力等,但也存在缺陷。研究发现,小波分析的一些性能恰好可以弥补BP网络的一些缺陷,因此,将小波分析与神经网络结合起来构成小波神经网络并用于汽车电控汽油机故障诊断。小波网络的隐层小波函数形式比Sigmoid函数复杂,可形成超椭球分割,从而能够造就更为细致的分割曲面,同时可以通过改变收缩因子和平移因子来增强分类能力;另外本文对小波神经网络提出了两个方面的改进。
1 小波神经网络
1.1 小波神经网络的基本理论
小波分析是近年来发展起来的数学理论,被认为是Fourier分析以来的重大突破。小波分析的定义为:
1.2 小波网络结构
小波神经网络如图1,其中学习样本经输入层投影压缩后作用于小波神经网络。
2 小波神经网络的改进
2.1 输出层函数的改进
在一般的小波神经网络中,总是应用Sigmoid函数作为输出层的激励函数。Sigmoid函数的输出值是0和1之间的数。当输出值接近于0或1时,网络输出几乎对网络出入失去敏感性。也就是说,改变权重已经几乎不起作用(这被称为函数饱和)。如果网络的实际输出值远离期望值,就很难对网络进行矫正了,从而使收敛速度变得很慢。因此本文用如(3)式所示的函数代替传统的Sigmoid函数。
2.2 代价函数的改进
本文对小波神经网络代价函数进行了改进,用"熵函数"代替传统的均方误差函数作为代价函数。使用熵函数E(d,y)=dlny+(1一d)]n(1一y)作为神经网络的代价函数,可使网络的各参数调整量在局部最小点附近不为零,即网络不会陷入局部最小点。因此可以使用"熵函数"代替均方误差函数作为网络的代价函数。
2.3 改进的网络学习算法
1)首先约定ωh0是第h个隐层节点阈值,ωωmo是第m个输出节点阈值(即x0=-1)。算法从输入层到输出层的顺序。
隐含层第h个节点的输入为
3.1 样本的提取
由于电控汽油机规格品种繁多且系统结构复杂,因此,汽油机的故障也多种多样。本文选取了11种有代表性的电控汽油机的故障现象,和与其对应的11种有代表性的故障原因分别为如表l所示:
用于汽车电控汽油机故障诊断的改进的小波网络的输入层有11个节点,对应与11种故障现象;输出层有11个节点,对应于11种故障原因。经过多次反复的试验,隐含层选择15个神经元即可满足误差要求。
本文分别有BP神经网络,未改进的小波神经网络和改进的小波神经网络度样本进行了训练,网络训练的误差曲线分别为图2、图3、图4。我们可以看出BP网络需要560步才能达到满足要求的误差,未改进的小波神经网络需要68步就能达到满足要求的误差,而改进的小波神经网络只需28步就能达到满足要求的误差。因此,可以得出改进的小波神经网络具有更强的逼近能力、网络学习收敛速度加快、能有效避免局部最小值问题等优点。
汽车电控汽油机故障诊断是通过研究故障征兆(特征向量)之间的关系来判断设备故障的。汽车电控汽油机故障诊断形式多种多样,故障产生的机理也非常复杂,加之实际因素的复杂性,故障与征兆之间表现出一种非常复杂的关系,即各类故障所反映的特征参数并不完全相同,这种关系很难用精确的数学模型来表示,这给现场诊断带来了极大的困难。由于人工神经网络具有高度的并行处理能力和极强的非线性映射能力,可以实现故障与征兆之间的非线性映射关系,因此在汽车电控汽油机故障诊断领域中显示了很大的应用潜力。其中用得最多的是基于Sigmoid输出函数的BP网络,尽管基于BP神经网络的故障诊断方法有许多优点,比如自学习能力强,不需要输入输出之间具体关系以及具有好的模型分类能力等,但也存在缺陷。研究发现,小波分析的一些性能恰好可以弥补BP网络的一些缺陷,因此,将小波分析与神经网络结合起来构成小波神经网络并用于汽车电控汽油机故障诊断。小波网络的隐层小波函数形式比Sigmoid函数复杂,可形成超椭球分割,从而能够造就更为细致的分割曲面,同时可以通过改变收缩因子和平移因子来增强分类能力;另外本文对小波神经网络提出了两个方面的改进。
1 小波神经网络
1.1 小波神经网络的基本理论
小波分析是近年来发展起来的数学理论,被认为是Fourier分析以来的重大突破。小波分析的定义为:
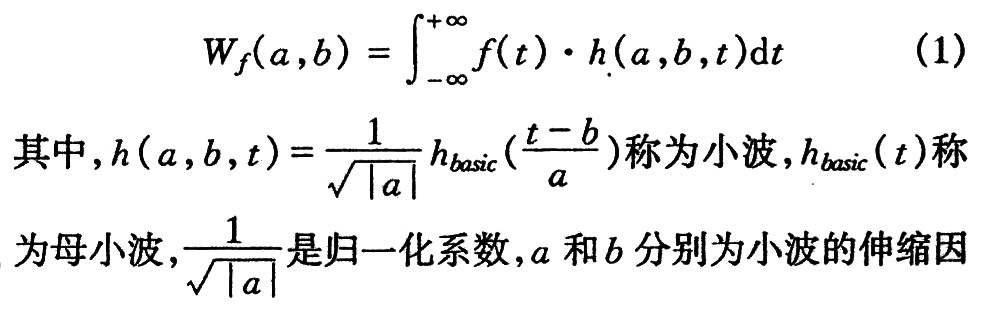
1.2 小波网络结构
小波神经网络如图1,其中学习样本经输入层投影压缩后作用于小波神经网络。

2 小波神经网络的改进
2.1 输出层函数的改进
在一般的小波神经网络中,总是应用Sigmoid函数作为输出层的激励函数。Sigmoid函数的输出值是0和1之间的数。当输出值接近于0或1时,网络输出几乎对网络出入失去敏感性。也就是说,改变权重已经几乎不起作用(这被称为函数饱和)。如果网络的实际输出值远离期望值,就很难对网络进行矫正了,从而使收敛速度变得很慢。因此本文用如(3)式所示的函数代替传统的Sigmoid函数。
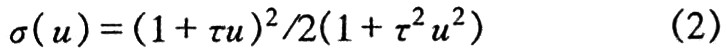
2.2 代价函数的改进
本文对小波神经网络代价函数进行了改进,用"熵函数"代替传统的均方误差函数作为代价函数。使用熵函数E(d,y)=dlny+(1一d)]n(1一y)作为神经网络的代价函数,可使网络的各参数调整量在局部最小点附近不为零,即网络不会陷入局部最小点。因此可以使用"熵函数"代替均方误差函数作为网络的代价函数。
2.3 改进的网络学习算法
1)首先约定ωh0是第h个隐层节点阈值,ωωmo是第m个输出节点阈值(即x0=-1)。算法从输入层到输出层的顺序。
隐含层第h个节点的输入为


3.1 样本的提取
由于电控汽油机规格品种繁多且系统结构复杂,因此,汽油机的故障也多种多样。本文选取了11种有代表性的电控汽油机的故障现象,和与其对应的11种有代表性的故障原因分别为如表l所示:

用于汽车电控汽油机故障诊断的改进的小波网络的输入层有11个节点,对应与11种故障现象;输出层有11个节点,对应于11种故障原因。经过多次反复的试验,隐含层选择15个神经元即可满足误差要求。

本文分别有BP神经网络,未改进的小波神经网络和改进的小波神经网络度样本进行了训练,网络训练的误差曲线分别为图2、图3、图4。我们可以看出BP网络需要560步才能达到满足要求的误差,未改进的小波神经网络需要68步就能达到满足要求的误差,而改进的小波神经网络只需28步就能达到满足要求的误差。因此,可以得出改进的小波神经网络具有更强的逼近能力、网络学习收敛速度加快、能有效避免局部最小值问题等优点。
- 电子技术的革新先锋(11-21)
- 利用FPGA协处理器优化汽车信息娱乐和信息通讯系统设计(01-24)
- 汽车收音机TDA7513射频电路应用指南(01-24)
- 基于NI Flex II创新技术的通用仪器可提供最高动态性能(01-24)
- 硬盘驱动器(HDD)新技术瞄准未来数字汽车应用(01-24)
- 当前汽车信息娱乐系统的软件技术需求分析(02-05)
