Help needed to solve these complex set of equations!!!
I am trying to model my circuit response. The frequency response and its equivalent circuit model is shown in the figures below.
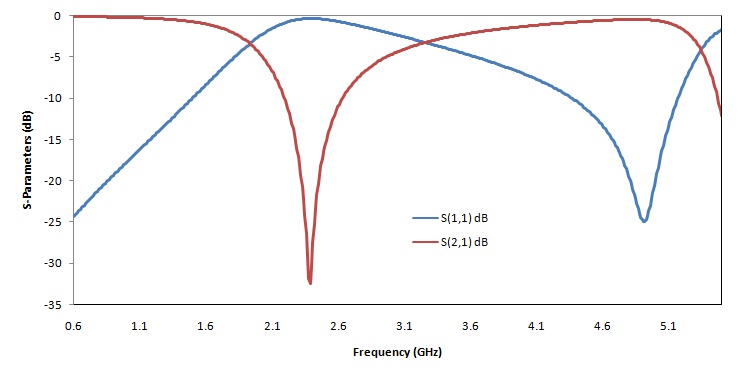
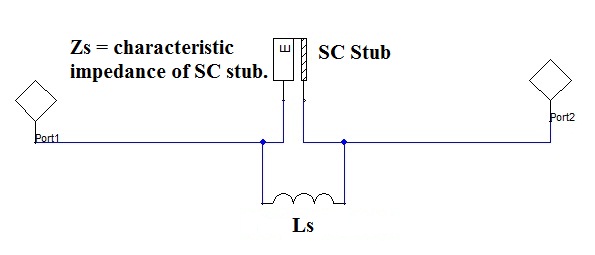
At the S21 dip (transmission zero - stop-band), the susceptance of the equivalent circuit = 0. Hence,
Ys cot (θ) - 1/(ω0 Ls) = 0
θ = electrical length of the stub, ω0 = Frequency at S21 dip. Ys = characteristic admittance of SC stub.
and at S11 dip (reflection zero - pass-band), the reactance of the equivalent circuit = 0. Hence,
(Zs ωp Ls tanθ)/(ωp Ls + Zs tanθ) = 0
This indicates that tanθ = 0. So, θ= pi, 2pi, 3pi, ...
At θ = pi, the SC stub produces a pass-band, and since θ=βl; β=ω/Vp, Vp= phase velocity:
θ=pi=(2pifp/Vp)lsc; fp= pass-band frequency, λg = guided wavelength, lsc = short circuited stub length. This gives lsc,
lsc = Vp/(2 fp) = λg/2
This gives lsc = 16.6mm for a pass-band frequency of 4.92 GHz.
Also, at 3-dB cutoff frequency (ωc), the susceptance of the equivalent circuit = susceptance of a low-pass filter prototype with one pole. Hence,
Ys cotθ + 1/(ωc Ls) = 1/100 ; ωc = 3-dB cut-off frequency.
So, we have three equations,
Ys cot (θ) - 1/(ω0 Ls) = 0 -> (1)
(Zs ωp Ls tanθ)/(ωp Ls + Zs tanθ) = 0 -> (2) or Ys cot (θ) - 1/(ω0 Ls) = ∞
Ys cotθ + 1/(ωc Ls) = 1/100. -> (3)
with lsc = 16.6mm at θ = pi.
Now, can anyone help me solve these equations to deduce the values of Zs, Ls.
Please help!
I didn't check the derivation of your equations: I assumed they are correct.
Form the first we can write:
Ys cot (θ) - 1/(ω0 Ls) = 0 -> Ys cot (θ) = 1/(ω0 Ls)
substituting this in the third:
1/(ω0 Ls) + 1/(ωc Ls) = 1/100 from which:
Ls=100*(1/ω0+1/ωc)
Looking at the second one we can only say that the numerator must be zero or the denominator must be infinite.
The numerator to be zero have to be zero at least one among Zs, ωp, Ls, tanθ then in this case if Zs<>0 we can desume nothing about it.
Denominator: the limits for Zs going to infinite and tanθ going to infinite are in both cases ωp Ls. Since we know ωp Ls is a finite quantity there is no chance to equate the equation to zero acting on the denominator
Then Zs have to be zero, or if the equation is get when tanθ=0 there is no way th desume Zs from it.
