Solve Helmoltz's equation using matlab

Hello,
Please, in the matlab command window How to solve the Helmoltz equation in the 2D space domain, in fact, I have to find proper functions and proper modes in an irregular geometry formed from a rectangle With two holes in the interior where the radius of holes and the width of the rectangle must change with each iteration.
thank you very much

I am not sure there is a way to do this from the command window, but you can easily program MATLAB to do what you want. It sounds like you are solving the Helmoltz equation as an eigen-value problem since you are asking about modes. There are many numerical methods for doing this including the finite-difference method, plane wave expansion method, finite element method, and more. For 2D, I highly recommend the finite-difference method. I think that will be your fastest and most versatile path to what you want. The finite-difference method is not the most effecient technique so as your problem size grows or you move into 3D, the finite-difference method will be less effective. For your problem, I suspect it will be great.

For a quick introduction to how I think you can solve you equation, take a look at Lecture 10 here (video + notes):

http://emlab.utep.edu/ee5390cem.htm

I would need to know more about your problem to advise you further.

Hope this helps!

Hello and thank you very much for answering me, in fact, I'm blocked for a long time in this problem, it's about analyze a Substrat Integrated Waveguide with the Boundary Integral Resonant Mode expansion method where I have to find coefficients Aij, Bij, Cij and Wm (in attached papers you can find formulas), for Aij and Bij it is easy while for Cij and Wm I have to solve Helmoltz's equation in a 2D domain presented in the figure below and because I am a beginner in matlab programming I can't find easealy the solution. thank you very much in advance.

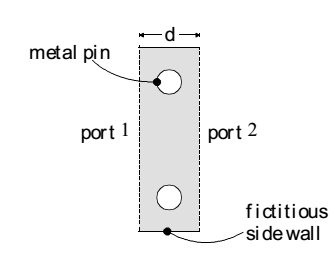
papers :

http://ieeexplore.ieee.org/document/508638/
http://ieeexplore.ieee.org/document/1031925/

if you can't get the papers please don't hesitate to contact me

Unfortunately, helping you with BI-RME is not something I can do. I have not implemented that method, but I do think it is a great technique for what you are doing. I took a look at the papers and I understand your problem. You have a periodic waveguide which complicates the physics a little bit. If you are new to this sort of thing, I think it is going to take considerable effort to develop your own BI-RME algorithm. I suspect, however, it is only the answer to this problem that you seek and not necessarily developing BI-RME.

If you were to solve this with the finite-difference method, there are three approaches. Here they are in order of what I think would work best:

1. Finite-Difference Frequency-Domain: You would essentially build one 3D unit cell of your waveguide in memory and solve it as Eigen-value problem. This will give you what the field looks like as well as the propagation constant of your mode, which I think is really what you are ultimately after if I read the second paper correctly. While I only discuss this in 2D, you can see the basic method in Lectures 10-12 in my previous link.

2. Finite-Difference Time-Domain -- This is essentially the same technique, but in the time-domain. This will allow you to simulate a much larger device with great memory efficiency. I did not dig deep enough to see the size of your problem relative to wavelength, but since you are using metals it is probably rather small.

3. Method of Lines -- If you could make a simplifying assumption that your vertical rods have a square cross section, the MoL would be very fast and efficient for you. Otherwise, it will be slower to resolve the curved boundaries of the vertical rods.

Do you have access to any commercial software? I ask because the structure you are simulating is somewhat complex. Calculating the propagation constant of a standard waveguide is simple, but yours is periodic so it is a little more complicated.

I just thought of how I would do this...First I would model your top plate, bottom plate, and dielectric fill as a slab waveguide. This is a 1D simulation and it would give the effective refractive index of the mode. Second, I would run a 2D finite-difference simulation of a grid filled with the effective refractive index you just calculated and add the metal posts. This would give the overall solution. I think it would be a pretty accurate simulation as along as the top and bottom plates are close enough to have the substrate support only a single mode. I would try to reproduce the results from these papers to ensure it is working.



If you want to try this finite-difference approach, I would do the following:

1. Watch Lectures 10-12.

2. Look through the electronics notes for these same lectures. I have made some revisions, additions, and improvements.

3. Write a MATLAB code that simulates a slab waveguide. Here is a link about doing this you will find extremely helpful...Topic 7c Slab Waveguide Analysis
http://emlab.utep.edu/ee4386_5301_CompMethEE.htm

4. Now write a 2D waveguide calculator like what you saw in Step 2. Because you have a periodic waveguide, there is a slight twist to how this simulation will be done.