[Basics] Why is (RF) current "flowing back" underneath the "forward line" ?
Let's talk about a ground plane:
I have a "problem" in thinking about how "return current" will flow. In any signal integrity & EMC book / advice one can find the statement that "RF current will flow back on a GND plane directly under the signal line". That is why you try to minimize the "current-loop", avoid plane splits, ...
Obviously they are talking about the maximum of current density in the return path. Maximum current density will occure on the path where minimal resistance exists (for the particular frequency). But why does the RF current see minimal impedance there?
Obviously minimum / optimal (?) impedance exists in the (physically longer) path following the RF-forward-trace than the physicall shortest way on the copper plane which is intuitivly thought to have the lowest resistance.
Similar on a microstrip line. Mircrostrip impedance is defined by tracewidth and distance to groundplane (and eps_r) in most modells. So obviously return-current must be flowing underneath the microstrip otherwise the "distance to groundplane"-term would be invalid.
So why do I have the lowest impedance directly underneath the forward-line (e.g. microstrip). A im interested in the physical effect and some ressources which would handle this topic. Seem I am stuck somewhere in the basics ...
Thank you in advance
Hi,
Do you know the eqivalent of a transmission line?
There are series inductors and parallel capacitors.
The serial inductors cause a magnetic filed ... (lossy)
And the capacitors need a feedback path...there is current flow back to the source of the signal.
Now imagine a single line. It has high distance to the feedback path, thus the parallel capacitance is low, resulting in high overall impedance.
Now imagine that the signal path and the ground plane (as it's return path) is in close proximity. The parallel capacitance obviously becomes high.
But now imagine the magnetic field. The signal path causes a field, with highest strength close at the trace.
And this causes current in the ground plane in opposite direction. Highest current close at the signal trace.
This return current causes a - because it is in opposite direction - magnetic field, in opposite direction, too.
Both magnetic fields compensate each other. It reduces the overall magnetic field around signal (and feedback) path.
Less magnetic field means less (magnetic) loss.
Also the compensated magnetic field acts like compensating the series inductance both in signal path and return path.
The path becomes lower impedance.
Now the (previously looking independent) signal and return path join to a common system.
Especially because of the inductive coupling the lowest impedance return path in a ground plane is in closest proximity to the signal line.
Klaus
In a real situation like yours, the current flow is not always that precisely under the line. Current also wants to takes the least impedance path, and in addition, there is skin effect that might push some amount of current to the ground plane edges.
I created an ADS Momentum testcase for your scenario, with 500μm trace over a large ground, at 1mm substrate thickness. The current flow on the ground plane then looks like this at 10MHz:
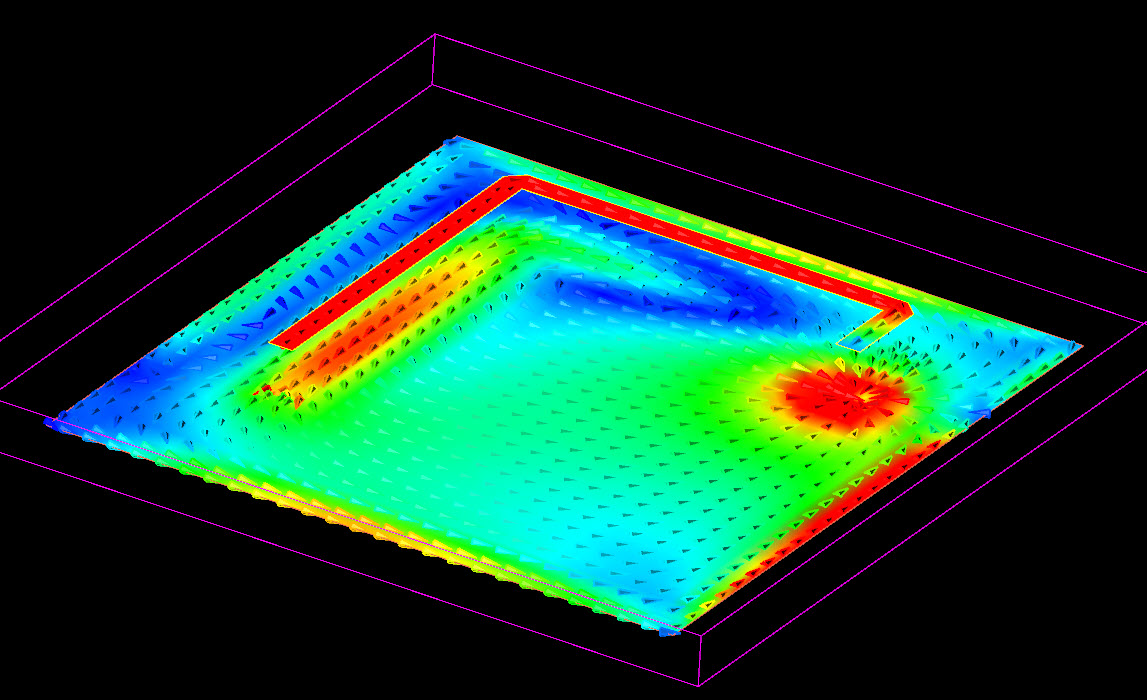
I tested and it looks very similar at other frequncies up to 1GHz.

It also looks similar at smaller substrate thickness 100μm instead of 1mm.
Hi,
thank you very much KlausST for your explanation and volker@muelhaus for your simulation. I appreciated very much your efforts.
@ KlausST: Regarding the weighting of the effects (inductive / capacitive). Could I say that inductive has the stronger effect due to the magnetic (nearfield) field dying of proportional 1/R^3 while the electric field (nearfield) proportional 1/R^2?
@ volker@muehlhaus: In the screenshot we see: color[blue:red] increasing = current density (surface current); arrows = vector of current flow (H-field monitor?) ? What boundary conditions did you use?
Thank you for your help
Hi,
hard to say. There may be other people with better explanations.
The combinatin of L and C (indeed mainly the trace width, distance and e_r) determines the characteristic impedance of the transmission line (in combination with the GND plane).
And you must not see this as static (or DC) current. So you need very high frequency .. and a minimum trace length to get the full effect of the characteristic impedance.
Klaus
Color indicates current density (Jxy), blue is low current and red is high current. Scale is linear. In addition, I included the arrows to show direction at one moment in time.
Boundary conditions are open, as always in Momentum.
One lumped vertical port on each end of the line between signal trace and ground plane.
I feel like some clarification may be in order. You're talking about transmission-line modes, in which the currents on the conductors (in this case, the microstrip and ground plane) are balanced (i.e., sum to zero; an expression of Lenz's law). Transmission-line modes require two conductors; and moreover the fields from one conductor are generally tightly linked to the fields on the other: this is why the current densities are mostly similar on the two conductors.
Obviously, you are observing the more real-life case with complex behavior such as currents coupling to other surface-wave modes, etc.; but the dominant behavior can still be seen to be the transmission-line mode.
Since the currents are balanced and strongly linked, it is generally not considered that there are "two" currents in a transmission-line mode -- there is only one, which travels one direction on the cross-section of one conductor, and the opposite way on the other. Similarly, there are not two impedances; there is only one -- the one seen by the TL mode. In cases where the "currents on the ground plane" diverge from those of the "currents on the micrsotrip"; this is simply what we would call coupling to other (non-transmission-line) modes. For example, a slot etched into the groundplane underneath a microstrip line is generally well-understood to generate surface-wave modes, which are not strongly bound between two conductors and may propagate away easily. The same may be said at corners, or other junctions, where the transmission-line model (typically derived assuming an infinitely long and unchanging line) does not hold.
Hope this helps!
