A reliable method to measure an inductor?
One method suggested to hook up a known resistance in series with the inductor and connect to an AC signal source. Change the freq. until the voltage on the resistor is equal to 1/2 the voltage on the AC source. Once that is achieved solve L=sqrt(3)/ωf. The problem is that the voltage on the resistor never dropped. I went from 0.1Hz - 2Mhz and nothing happened (anyway the formula seems strange is no explanation is given).
My inductor is about 40 Ohm R and about 0.550H @ 300Hz according to my DMM with inductance scale. My problem is that this is not enough for me and I would like to measure the inductance or impedance of the coil at different freq. since the core is ferrite and the inductor probably does not obey xL=ωL.
I'll appreciate feedback on this! :)
Wrong assumption. Real impedance part is representing DC copper resistance, frequency dependent skin and proximity effect losses and core losses. Increasing R (I presume you are referring to a series circuit Z = R + jX) can be expected for any inductor below it's self resonance frequency.
Obvious explanation: Unsuitable (too high) resistance value.
Refer to a AC circuit textbook instead of copying badly explained formulas. See e.g. http://www.ibiblio.org/kuphaldt/elec...html#02062.png
Why? I would assume constant L in a first order.
FvM -
I am taking the measurements at freq. between 20Hz and 18.5KHz, at these freq. skin effect is almost non existing. Even telephone lines which are usually 24AWG lose less than 1 Ohm @ 10KHz. However I do agree that eddy currents might mess with the effective resistance of the wire and it might be a little different from the wire resistance. How much does it change? I don't know! But I can pull the wire from an inductor and measure it's R before and after and see if the effect is significant!
As said, skin effect is just one of several factors that cause a frequency dependant R part of impedance. In contrast to the other factors, skin effect can be rather exactly calculated, so you won't need to measure it.
If you give an idea of wire gauge, number of windings and core type/size, it would be more easy to estimate expectable results.
On the other hand, if you're unable to indentify the parts inductance in a trivial LR circuit by measuring the partial voltages and solving it graphically in a vector diagram, this may be also indicate a component fault, preferably a windings short. Or a problem in your measurement setup.
I have a few of these inductors, they are all alike (with little tolerances) so I assume the wingdings are OK. What resistor size do I need for this setup? I tried to connect a resistor is series with the inductor and to an AC source. I subtracts the voltage across the inductor from the voltage on the AC source and divide by the resistor to get current through the circuit. I divide the voltage across the inductor by the current to get impedance. Since I know the R at that freq. (300Hz) I can solve for xL and inductance. I get about 20% from the DMM reading which is not bad but far from being useful.
You can't substract magnitudes of voltages with different phase, please refer to the linked explanation in Lessons In Electric Circuits . You need to measure the voltage across the resistor directly.
You are correct, my mistake!
By the way, one way to check my measurements is to take a known capacitor and the inductor and calculate oscillation freq. and check if I can predict it accurately no?
Yes, making a resonant circuit is simple way to determine inductance. You can use a simple emitter couped oscillator, a variable resistor in place of R1 allows to adjust the gain (respectively negative resistance) according to the circuit losses.
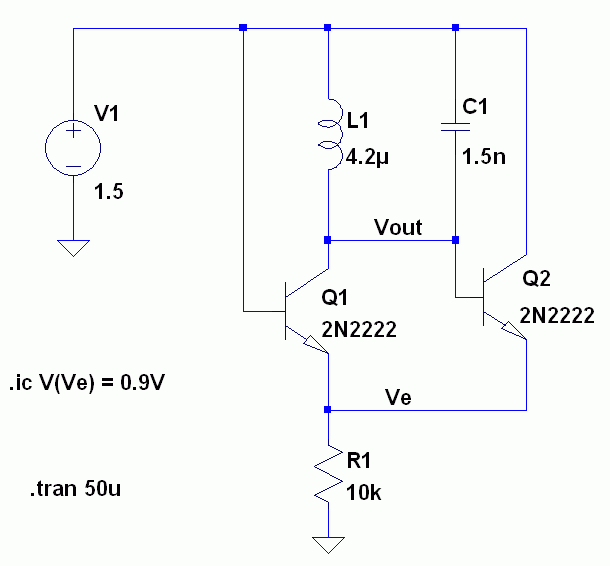
Thank you very much! I will try to build this circuit. I also looked at a Clapp oscillator. Do you have the formula for the schematic you posted?
Also, this will give me L, but at what freq.? How can I use this info to determine inductance at other freq.?
L and C are determing the resonance frequency, ω = √LC is valid for all LC resonant circuits. You need to vary C to get a suitable frequency range, that's all.
R should be limited to e.g. 100 ohm minimal to protect the transistors and can range up some 10 kohms. The circuit starts to oscillate when decreasing R. Highest R value with stable oscillation give best measurement. Two terminal resonator connection and Hz to MHz frequency range with wide gain variation is the advantage of this circuit.
I've built the circuit on a breadboard (not ideal but did the trick). After calculating the inductance I got a value of 620mH. I checked the inductor on the PC impedance meter at the same freq. I've read on the scope (was around 638Hz) and got 610mH. I think the difference is very small and looks normal to me as inductors usually won't measure the same on different instruments with different fixtures. How can I measure inductance at different freq.? I guess a resonant circuit is out of the question because it has a set freq.
By the way - I am assuming here that the inductance value I calculated from the circuit is true at 640Hz because that's the resonant freq. of the circuit. This is correct, right?
You have used a capacitor of 100 nF for the resonant circuit. By varying the capacitance, you get different resonance frequencies, in so far it is possible to measure the inductance at different frequencies. You need to consider the specified capacitor tolerance which sets a limit to measurement accuracy, it may be easily 5 or 10 % or even more. Another point is the windings capacitance which causes a self resonance frequency without connecting external capacitors.
Yes, I actually measured the capacitor and found out it is 100.6nF. By solving the equation according to the freq. measured with my scope I was able to get within 3% from what my PC meter suggested. I have built the circuit on a bread-board and it might have added some capacitance in parallel, lowering the circuit freq. which gave a little higher inductance. I will post the plot of the inductor once it is done. Thanks!
