请教各位一个问题,异步复位和同步复位实现起来有啥区别啊。
就是时序系统中,异步复位和同步复位的区别。
书里说,异步复位,不需要时钟,复位信号到后,就能实现复位。
而同步复位,是需要复位信号到达时,时钟边沿采样,才实现复位。
代价的话,异步复位较小,但受OCV等影响较大。
而同步复位,代价较大,但复位同步性好。
同步复位实现的话,在reg前,加一个用reset复位信号控制的二选一逻辑即可。
那异步如果代价较小的话,又是什么如何实现的呢?
我查到的,就是以上这些,可能不对,也可能和实际应用差得远。
哪位在工程中接触过这两种复位方式的前辈,能否彻底指点一下:
1,这两种复位方式,是用哪种硬件结构实现的?
2,这两种方式,分别应用在什么情况下?各有什么优缺点呢。
非常感谢大家啦
异步复位就是复位信号直接连到FF的异步复位端,信号随到随复位,不需要时钟。在没有时钟时要复位的情况下,一定得用异步复位。如果对复位信号没有特别要求时,在后端比较容易做。
同步复位其实就是把复位信号当作一个数据的输入,同其他输入混在一起后,连到FF的D端。所以它需要时钟才工作,而且在后端要做一个reset tree,无形中给后端的时序收敛增添了困难
非常感谢涛哥。
不过,我还有个疑问。如果说同步复位,是和数据路径做到一起的。那如果要实现同步复位,直接利用时钟树的信号不就可以了吗?
为什么还要做复位树呢,用时钟树就能代替吧。
而异步复位,因为没有时钟,要保证复位信号达到时,所有的FF都复位,是不是应该做一个延时基本平衡的复位树来保证复位状态呢。
你去看看那篇经典的SNUG文章吧
学习了,谢谢咯
现在为了简单,都是异步复位吧,后端做起来也简单,
reset tree只是 修trans, 不管 latency, 就是reset迟早能够全部复位的意思
不管多久,
同步复位有点烦
在我看来复位信号的recovery和removel 和 一般信号的setup和 hold
一个意思啊那按一般的信号加约束 满足setup和hold 就行了啊
对不对啊求指点
请问为什么异步复位会比同步复位容易受OCV影响?按我理解的话同步复位才是会影响timing。
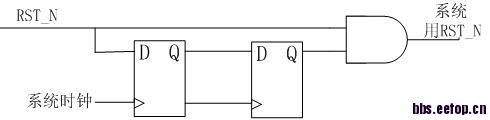
以前看到过这样一个复位电路,
大家分析一下,
这个和通常使用的异步复位同步释放电路相比有什么优缺点。
我个人觉得,好像也就是同步释放后,RST_N信号上相对于时钟多了一个与门的迟延,
也应该能起到异步复位同步释放的效果。
不知道时序分析的时候,是不是会麻烦一些。
低电平不就直接过去了?受时钟控制么?
刚刚画了一下,res的上升沿是受时钟控制的,所以res解除的时候是时钟同步的。
估计这样可以验证recovery和remove了吧。
不知道对否。
异步复位信号生效时一般会维持好多拍,所以可以不管时钟,直接复位寄存器。
异步复位信号解除时要让所有的寄存器尽可能在同一个时钟节拍内解除复位,并且满足寄存器的removal时间。
9楼图中寄存器的作用是让异步复位信号转换成本时钟域的同步信号,采用两级寄存器是为了降低异步复位信号与时钟同时变化时输出亚稳态的几率,与门的作用是异步复位同步释放。
真心学习了很多
正在受这个问题的后端困扰
你好,我想借帖子问一下, 因为异步复位信号一般是input,那怎么加set_input_delay呢?还有就是如果不做synchronizer, 怎么才能知道recovery/removal是满足的?
面积:同步复位是在D端加一个AND/OR;异步复位是把两个Latch中间的反相器变成NAND/NOR还要增加一个反相器。DFF级别的面积差别实在不大
最小脉宽:异步复位的最小脉宽一般会比时钟最小脉宽大很多,一般会到ns级;同步复位的最小脉宽就是setup+hold,肯定是在ps级。
对抗OCV:异步复位期间把时钟关掉可以消除OCV带来的挑战。如果设计不允许异步复位期间把时钟关掉(如:存在没有复位的寄存器,等),那同步复位和异步复位遇到的OCV挑战是相似的,而且异步复位由于最小脉宽较严还会对占空比带来要求。不过,假如你的时钟频率在500MHz以下,则不大可能遇到复位带来的OCV冲击。
同步复位带来的最大问题是,RTL中看似同步复位的代码并不一定会综合成同步复位,使网表不简明。即,RTL中的第一个if...else并不一定是综合后物理上最短的路径。
深入~
请问您说的异步复位的最小脉宽 具体指的是什么?说的是异步复位所要持续的最短时长吗?
RTL中看似同步复位的代码并不一定会综合成同步复位,使网表不简明。即,RTL中的第一个if...else并不一定是综合后物理上最短的路径。
为什么呢?
assign y = s1 ? c : (s0 ? b :a);
assign y = (~s1 & s0) ? b : (s1 ? c : a);
这两句功能是完全一样的,但“看起来”第二句b->y的路径变短了。
好讨论,学习了
学到很多,谢谢
能推荐一下那篇文章叫什么名字吗?谢谢
