怎样实现1/3？

先在被除数后补5个‘0’，然后做除法。
简单点就循环减法，复杂点就做移位除法。

    自己写的话? 用这个除法器的资料啊?

   比如 1/3 转化为100000 / 11 的出来的结果为001001 ? 那么怎么转换成0.33333呢?

把1/3=0.33...变成乘法，即一个数乘以0.33...

    再左移5位，还原。

    那还不是0.3333啊? 我的想法是在FPGA直接可以做出1/3 = 0.33333的，包括0.33333也是FPGA实现的

补5个‘0’表示小数点左移了5b,"01"/"11" 变成  b"01.00000"/b"11" = b"00.01010" = 0.25+0.0625 = 0.3125 约= 0.33*32
这个是保留二进制的小数点后5位的方法，突然发现你是要十进制的小数点后5位啊，那得补17个‘0’。
如果除数是固定等于3： /3 = *0.33333 = *0.25 + *0.0625 + *0.015625 + *0.0xxx 逼近

    如楼上所说。精确到小数点后5位，那需要10^5对2取对数（约为16.6取整17），即二进制数后面加17个0。

    那么这个 *0.5 ，*0.25 ,*0.125,
  在FPGA怎么表示呢? 是右移啊? 还是 ?
谢谢了

   恩，是移动10-5 ， 现在我在尝试一下啊，因为现在要做 泰勒公式的FPGA实现，实现7级展开。
你有好的方法吗?

    1.用流水线方式
    2.泰勒公式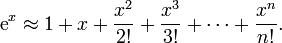

    3.再你的FPGA有什么函数可以调用的?

对无符号数而言
    *0.5   = >>1
    *0.25 = >>2

先计算好x/1, x/2, x/3, x/4, x/5, /6, x/7,第一项与第二项相乘即x^2/2！, 第二项与第3项相乘即x^2/3！,依次类推，可以优化算法。优点计算时间短，缺点精度会受到影响。

    OK,好的，谢谢了，我尝试一下啊，

    好的，谢谢了！呵呵。