专用短波接收机射频前端预选滤波器的设计与实现

为了得到性能较好的射频接收机前端，滤除接收机中的各种干扰信号，保留有用信号，必须在接收机前端适合的地方放置滤波器。尤其是放置于系统第一级的预选滤波器，它的性能好坏直接影响了整个接收机射频前端的噪声系数。通过分析N 级级联系统噪声系数方程可知，必须将预选滤波器的损耗降到最低，同时还必须使其具有系统需要的选择性。

1、预选滤波器的选择

由于预选滤波器处于整个射频前端系统的第一级，其性能对整个接收机系统产生极大的影响，考虑到系统的线性度（避免非线性误差带来噪声），预选滤波器中不应有任何有源器件，因此该滤波器应设计为无源LC滤波器^[1]。

同时，对于专用短波接收机系统来说线性的相位响应（相移）要比陡峭的衰减或幅度变化更为关键，而且线性的相移和陡峭的幅度变化是相互冲突的。综合考虑其相互影响并结合系统要求，文中设计选择了衰减曲线中波纹最小的最大平滑巴特沃兹（Butterworth）带通滤波器。

2、预选滤波器的设计与实现

2.1、预选滤波器的设计方法

目前，模拟带通滤波器的设计方法都是将要设计的滤波器的技术指标通过某种频率转变关系转换成模拟低通滤波器的技术指标，并依据这些技术指标设计出低通滤波器的转移函数，然后再依据频率转换关系变成所要设计的滤波器的转移函数^[2]。

模拟带通滤波器的4个频率参数是Ω_sl、Ω₁、Ω₃、Ω_sh，其中Ω₁、Ω₃ 分别是带通的下限与上限频率，Ω_sl是下阻带的上限频率，Ω_sh是上阻带的下限频率，首先要将它们做归一化处理。

定义Ω_BW =Ω₃ -Ω₁ 为带通的带宽，并以此为参考频率对Ω轴做归一化处理，即
η_sl =Ω_sl /Ω_BW，η_sl =Ω_sh /Ω_BW，
η₁ =Ω1 /Ω_BW，η₃ =Ω₃ /Ω_BW。

再定义Ω=Ω₁Ω₃ 为带通的中心频率，归一化的η=η₁η₃，从而可以得出其归一化的幅频特性H（jη）及归一化的低通幅频特性| G（jλ）|，进而可以得出η和λ的一些主要对应关系。在η₂ - η₃ 之间找一点η，它在λ轴上对应的点应在0 - λ_P 之间，由于η₃ =η /η₁，那么η在η轴上对应的点应是η/η，而λ在λ轴上对应的点应是-λ。这样又可找到η与λ的转换关系为

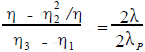（1）

由于η₃ -η₁ = 1，λ_P = 1，所以有

（2）

从而实现了频率转换。利用所得到的低通滤波器技术指标λ_P、λ_s、α_P、α_s，可设计出滤波器的转移函数G（p）。由

（3）

可得

（4）

这样，所需的带通滤波器的传递函数可以求出。

通过上述方法可以将巴特沃兹模拟带通滤波器的设计转化成巴特沃兹模拟低通滤波器的设计^[3]。注意，N 阶的低通滤波器转换到带通后，阶次变为2N。

给定模拟低通滤波器的技术指标α_p、Ω_p、α_s、Ω_s，其中αp 为通带内允许的最大衰减，α_s 为阻带内应达到的最小衰减，α_p、α_s的单位为dB，Ω_p 为通带上限角频率，Ω_s 为阻带下限角频率^[4]。

α_p、α_s 都是Ω的函数，它们的大小取决于|G（jΩ）|的形状，为此，定义一个衰减函数α（Ω），即

（5）

这样，式（5）把低通模拟滤波器的4个技术指标和滤波器的幅平方特性联系了起来。

由于每一个滤波器的频率范围存在很大差别。为了使设计规范化，需要将滤波器的频率参数作归一化处理。设所给定的实际频率为Ω（或f），归一化后的频率为λ，对低通滤波器，令

λ =Ω /Ω_p（6）

令归一化复数变量为p，p = jλ，显然

p = jλ = jΩ /Ω_p = s /Ω_p（7）

巴特沃兹低通模拟滤波器的设计可以按以下3个步骤来进行。

1）将实际频率Ω归一化

得归一化幅平方特性

（8）

由此可以看出|G（jλ）|²（或|G（jΩ |²）中只有2个参数C和N，N 是滤波器的阶次。

2）求C和N

由（5）式得

α（λ）= 101g（1 + C²λ^2N），（9）

则公式，

（10）

因为λ_p = 1，所以

（11）

这样C和N 可求。

若令α_p = 3 dB，则C = 1，这样巴特沃兹低通模拟滤波器的设计就只剩下一个参数N。

3）确定G（s）

因为p = jλ，有

（12）

由1 +（-1）^Np^2N = 0

解得

（13）
 
这样，G（p）G（- p）的2N 个极点等分在s平面半径为一的圆上，相距为（π/N）rad。
 
为了保证所设计的滤波器是稳定的，应把左平面的极点赋予G（p），即
 
（14）