异步电机无速度传感器矢量控制系统研究

对于高性能的磁场定向控制系统，速度闭环是必不可少的，转速闭环需要实时的电机转速，目前速度反馈量的检测多是采用光电脉冲编码器、旋转变压器或测速发电机。但是，许多场合下不允许安装任何速度传感器，此外安装速度传感器在一定程度上降低了系统的可靠性。因此，无速度传感器控制的高性能通用变频器是当前全世界自动化技术和节能应用中受到普遍关心的产品和开发课题。无速度传感器磁场定向矢量控制技术的核心是如何准确的获取磁场定向角以及电机的转速信息。2000年，日本电气学会调查了日本各大电气公司生产的无速度传感器控制的通用变频器，把无速度传感器控制方式分为4类：定子电流转矩分量误差补偿法；感应电动势计算法；模型参考自适应(MRAS)法；转子磁链角速度计算法。其中感应电动势计算法和转子磁链角速度计算法是基于电机数学模型来计算转速，属于开环计算转速，转速计算的精确度容易受到干扰，而定子电流转矩分量误差补偿法与MRAS法是基于闭环控制作用构造转速，可以抑制这种干扰。定子电流转矩分量误差补偿法结构简单，已在一些变频器产品中得到应用，但所产生的动态转速准确性欠佳。MRAS法则基于转子磁链观测电压模型与电流模型构造转速辨识模型，算法简单，能实时跟踪电机转速变化。在此结合应用SVPWM技术构建了转子磁场定向无速度传感器矢量控制系统，采用MRAS法得到转子转速辨识模型，对速度进行估算。利用Matlab／Simulink对系统进行仿真，以验证所设计的控制系统的性能。

　　l 异步电机转子磁链及转子转速的估算

　　1．1 转子磁链的估算

　　在转子磁场定向异步电机元速度传感器矢量控制系统中，转子磁链难以直接测量。实际采用的是其观测值，只有当观测值与实际值相等时，才能达到矢量控制的有效性。因此，准确的获得转子磁链值是实现矢量控制的关键。

　　按转子磁场定向异步电机数学模型可推导出磁链的计算公式如下(推导过程略)，其中磁链的估算包括其幅值和角度。

　　式中：ψr为转子磁链；ωs为转差角速度；ωr为转子转速；isd，isq为定子d，q轴电流；Tr为转子时间常数，Tr=Lr／Rr，Lm为定转子互感；Lr为转子电感；Rr为转子电阻；θ为磁链角度，P=du／dt。

　　1．2 转子转速的估算

　　采用MRAS方法对转子转速进行估计。基本思想是：在异步电机两相静止坐标系下，以不含有转速变量的转子磁链观测电压模型为参考模型，含有转速变量的转子磁链观测电流模型为可调模型，利用波波夫超稳定性理论设计自适应辨识规律，从而实现对转子转速进行估计。异步电机两相静止α，β坐标系下转子磁链观测模型如下两式所示：

　　式(2)不含有转速变量，作为参考模型，式(3)含有转速变量作为可调模型。在设计模型参考自适应律时，将电流模型转速变量看成常数作为参考模型，式(3)作为并联估计模型：从而得到误差方程：

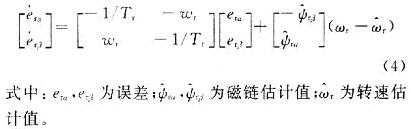
　　依据波波夫超稳定性理论求解稳态误差，设计出比例加积分的自适应律为：

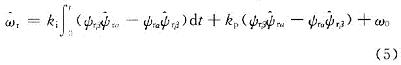
　　式中：ki，kp为可调系数；ω0为给定估算转速初值，可以任意给定，取ω0=0。至此，构建出基于模型参考自适应方法的转速辨识模型。

　　2 仿真模型的建立

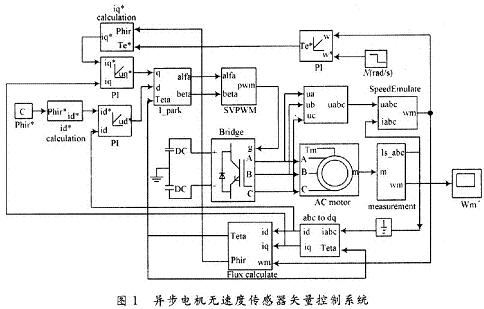
　　异步电机无速度传感器矢量控制系统如图1所示，主要包括三相异步电机模块，SVPWM模块，PI模块，坐标变换模块，转子磁链估算模块，转子转速估算模块，逆变器模块等。该系统主电路采用SVPWM调制逆变器，控制电路中，给定转速与估算转速经过速度调节器得到转矩，与估算磁链值计算得到电流isq，经过电流调节器，再经过PARK逆变换得到两相静止电压，经过SVPWM调制，控制逆变器电压输出，进而控制三相异步电机。SVPwM控制的基本思想是将电机与逆变器看成一个整体，最终在电机内部形成圆形磁场，以达到更好的控制效果，SVPWM控制的仿真模型如图2所示。

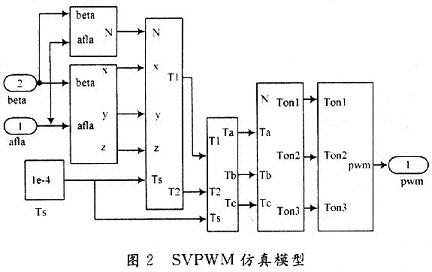
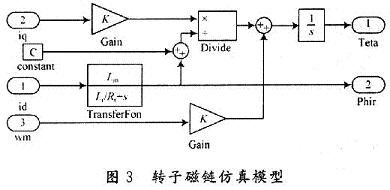
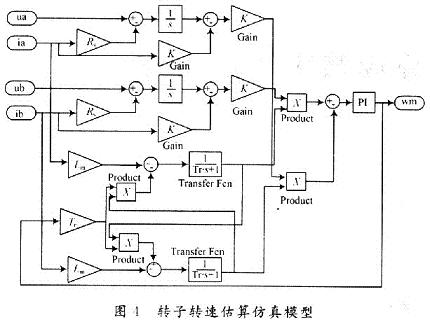
异步电机转子磁链依据式(1)估算，仿真模型如图3所示。异步电机转子转速估算模型如图4所示，依据转子磁链观测电压模型与电流模型，采用MRAS法辨识。在仿真调试过程中，加入一阶传函近似为低通滤波器，对输出估算转速进行处理。仿真结果有明显的改善。

　　3 仿真结果分析

无速度传感器矢量控制仿真系统所采用电机的参数为：Pn=2．2 kW，Rs=O．435Ω，Rr=O．816Ω，Lm=0．0693H，L1s=L1r=0．002H，转动惯量J=O．02kg·m2，极对数Np=1。电机空载运行，初始给定速度为120 rad／s，当t=O．5s时，改变速度为60 rad／s。在启动时，当t=O.1-2s时，转子转速就达到了稳定，当给定速度在t=O．5s时发生变化，转速输出在t=O．56s时再次达到稳定，仿真结果如