摩尔定律消退后 计算机行业将如何发展？

摩尔定律支配了计算领域 44 年的时间，今年终于宣告终结。在这之后计算领域会发生什么事？得益于半导体和芯片技术而高度繁荣的手机、PC 产业，会受到怎样的影响？

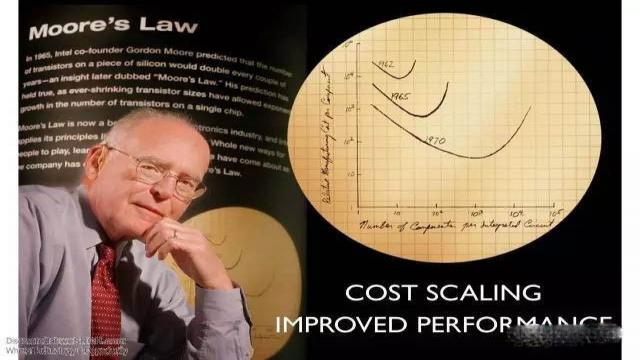
　　摩尔定律最早由英特尔联合创始人 Gordon Moore 提出，内容是：当价格不变时，集成电路上可容纳的元器件数量约每隔 18-24 个月就会增加一倍，性能也将提升一倍。后面 Moore 修正了模型，变为：单位面积芯片上的晶体管数量每两年能实现翻番。

　　摩尔定律消退后 计算机行业将如何发展？

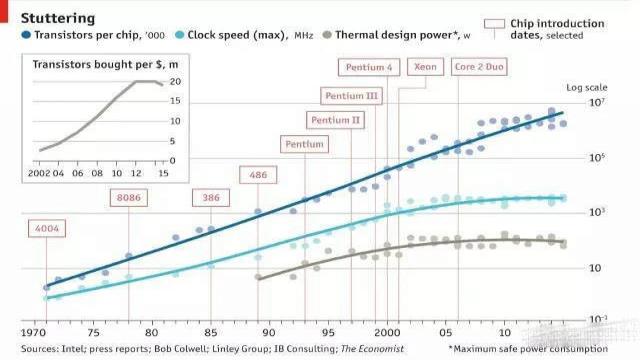
　　谁也想不到，这个 1971 年提出的定律，竟能支配计算领域长达 44 年的时间。直到今天，英特尔官方宣布，放弃过去十年坚持的 Tick-Tock 处理器发展模式，通过延长制造工艺的生命周期，将之前的处理器研发周期从 "两步" 变成 "三步"：

　　制程工艺（PROCESS）

　　架构更新（ARCHITECTURE）

　　优化（OPTIMIZATION）。

　　英特尔 CEO Brian Krzanich 表示，"我们的更新周期已经从 2 年延长到了 2 年半。"

　　这意味着对于英特尔而言，摩尔定律已经失效。

　　摩尔定律消退后 计算机行业将如何发展？

　　摩尔定律的失效，并不出乎人们的意料。微软研究院的副总裁 Peter Lee 曾经开玩笑说："预测摩尔定律将会失效的人数，每 2 年都会翻上一番。" 而在英特尔官方宣布放弃追求摩尔定律曲线的时候，这一天也就到来了。

　　摩尔定律对整个计算产业有着举足轻重的影响。我们最为关心的是，在摩尔定律之后，计算领域会发生什么改变？答案就在以下十大方向，包括：

　　1、从根本上改变芯片的设计：包括 3D 维度的芯片设计、周围栅极、量子隧穿效应等。

　　2、寻找硅材料的替代品：包括硅 - 锗（SiGe）、合金隧道、III-V 材料设计、石墨烯、自旋晶体管等。

　　3、从现有晶体管寻找出路：多核芯片、特制芯片、新品种芯片。

　　4、计算框架的变革：量子计算框架、光通信、量子阱晶体管、神经形态计算、近似计算。

　　摩尔定律的黄昏将带来机遇、混乱和大量的摧毁性创意。一个原本依赖于大量设备稳步升级的行业将被撕碎。那么计算的未来，究竟会怎样发展？

　　摩尔定律背后的物理瓶颈

　　摩尔定律的黄昏与计算行业的黎明摩尔定律并不是一套 "物理定律"，而是大公司定义的经济规则。在以英特尔为首的芯片公司定义了一套游戏规则，要在两年的时间里把晶体管数量增加一倍，同时成本减少一半。

　　过去这套经济规则并没有违反物理定律。研究人员发现，当晶体管在体积变小时，性能也会变得更好：

　　体积较小的晶体管在开启关闭时需要的能量更少、速度也更快。这意味着你可以使用更多更快的晶体管，而无需付出更多能量或产生更多废热，因此芯片可以在越做越大的同时、性能也越来越好。

　　能做到这一点的公司获得了成功，而做不到的则逐渐被历史淘汰。但当晶体管尺度变小到小型化的极限 "原子尺寸" 的时候，事情变得和人们期待的有所不同。

　　在这种原子尺寸下，现代晶体管的源极和漏极非常接近，大约是 20 纳米的量级。这会引起隧道泄露，剩余电流能够在装置关闭的时候通过，浪费了电量和产生不必要的热量。

　　从这个来源产生的热量会导致严重的问题。许多现代芯片都必须低于最高的速度运行，或者周期性的关闭部分开关以避免过热，这限制了它们的性能表现。

　　现在的芯片晶体管间距已经在 10 纳米左右的量级了。减小间距会带来非线性的成本增加，根据国际商务战略公司 CEO Handel Jones 的估计，当业界能够生产晶体管间距 5 纳米的芯片时（根据过去的增长率来看可能出现在 2020年 代早期），晶圆厂的成本可能飙升到超过 160 亿美元，这是英特尔目前年营收的三分之一。

　　2015 年英特尔的年营收是 554 亿美元，只比 2011 年增长了 2%。这种营收的缓慢增长与成本的大幅上涨，带来了显而易见的结论：从经济的角度来看，摩尔定律已经过时了。

摩尔定律消退后 计算机行业将如何发展？

　　摩尔定律的下一步

　　很显然，传统的芯片设计方案已经到达了瓶颈。要找到下一代芯片，会需要两个广泛的变化。

　　1、晶体管的设计必须从根本改变；

　　2、行业必须找到硅的替代品，因为它的电学属性已经被推到了极限。

　　一、根本改变芯片设计

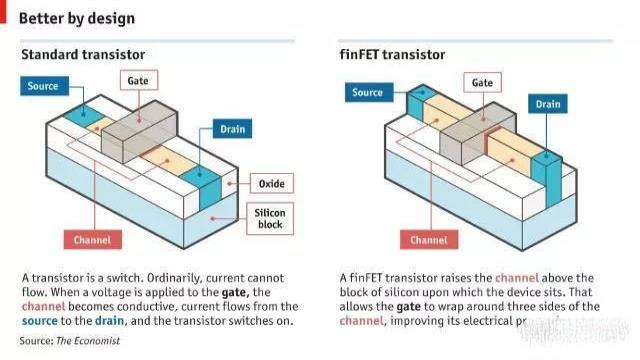
　　（1）第三个维度

　　摩尔定律消退后 计算机行业将如何发展？

针对这个问题，一个解决方案是重新设计隧道和栅极。按照惯例，晶体管一直是平面的，但自从 2012 年之后，英特尔给产品增加了第三个维度。要启用它来生产出只有 22 纳米距离的芯片，它切换到了被称为 "finFETch" 的晶体管。